Łuki Talesa»Zadanie 5
o zadaniu...
- Zadanie pochodzi z artykułu Łuki Talesa
- Publikacja w Delcie: wrzesień 2017
- Publikacja elektroniczna: 1 września 2017
Skonstruuj trójkąt 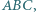 mając dane punkty
mając dane punkty 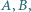 kąt przy wierzchołku
kąt przy wierzchołku 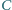 oraz długość środkowej
oraz długość środkowej 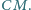 Ile rozwiązań może mieć to zadanie?
Ile rozwiązań może mieć to zadanie?
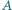 i
i 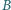 należą do wnętrza kąta ostrego
należą do wnętrza kąta ostrego 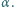 Skonstruuj taki trójkąt równoramienny, aby punkty
Skonstruuj taki trójkąt równoramienny, aby punkty 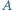 i
i 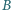 należały do różnych jego ramion, aby podstawa tego trójkąta była zawarta w jednym z ramion kąta
należały do różnych jego ramion, aby podstawa tego trójkąta była zawarta w jednym z ramion kąta 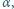 a wierzchołek należał do drugiego z ramion.
a wierzchołek należał do drugiego z ramion.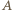 symetrycznie w jednym z ramion kąta, otrzymując
symetrycznie w jednym z ramion kąta, otrzymując 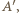 narysuj łuk Talesa dla odcinka
narysuj łuk Talesa dla odcinka 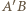 i kąta
i kąta 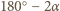 i rozważ odpowiedni jego punkt przecięcia z wybranym wcześniej ramieniem kąta.
i rozważ odpowiedni jego punkt przecięcia z wybranym wcześniej ramieniem kąta.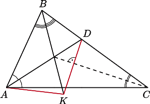
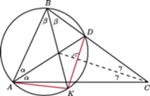
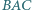 trójkąta
trójkąta 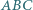 przecina bok
przecina bok 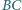 w punkcie
w punkcie 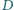 (rys.). Prosta przechodząca przez punkt
(rys.). Prosta przechodząca przez punkt 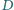 i prostopadła do dwusiecznej kąta
i prostopadła do dwusiecznej kąta 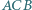 przecina dwusieczną kąta
przecina dwusieczną kąta 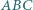 w punkcie
w punkcie 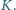 Udowodnić, że
Udowodnić, że 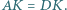
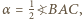
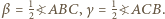 Wówczas
Wówczas 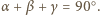 Mamy
Mamy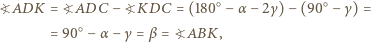
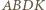 można opisać okrąg. Z rowności
można opisać okrąg. Z rowności 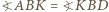 wynika zatem, że
wynika zatem, że 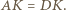
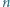 będzie liczbą naturalną większą od 4. Udowodnić, że w elipsę o półosiach różnej długości nie można wpisać
będzie liczbą naturalną większą od 4. Udowodnić, że w elipsę o półosiach różnej długości nie można wpisać 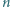 -kąta foremnego.
-kąta foremnego.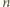 -kącie foremnym przecinałby elipsę przynajmniej w pięciu punktach, a to nie jest możliwe.
-kącie foremnym przecinałby elipsę przynajmniej w pięciu punktach, a to nie jest możliwe.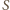 oznacza pole trójkąta,
oznacza pole trójkąta, 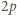 - jego obwód,
- jego obwód,  - promień okręgu wpisanego, zaś
- promień okręgu wpisanego, zaś 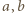 i
i  - długości boków, to wówczas
- długości boków, to wówczas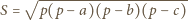
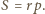 Z tych wzorów wynika, że
Z tych wzorów wynika, że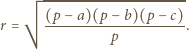
 o boku długości
o boku długości 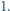 Przekątne
Przekątne 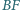 i
i 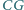 przecinają się w punkcie
przecinają się w punkcie 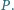 Znaleźć długość odcinka
Znaleźć długość odcinka 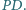
 przez
przez 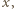 a krótszej i dłuższej przekątnej danego siedmiokąta foremnego odpowiednio przez
a krótszej i dłuższej przekątnej danego siedmiokąta foremnego odpowiednio przez 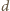 i
i 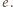 Wówczas na mocy twierdzenia Ptolemeusza, zastosowanego do trapezu równoramiennego
Wówczas na mocy twierdzenia Ptolemeusza, zastosowanego do trapezu równoramiennego 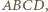 uzyskujemy
uzyskujemy 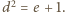
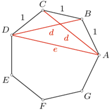
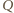 będzie takim punktem, że czworokąt
będzie takim punktem, że czworokąt 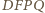 jest równoległobokiem. Wówczas
jest równoległobokiem. Wówczas 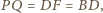 więc trapez
więc trapez 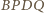 jest równoramienny. Stosując do niego twierdzenie Ptolemeusza, otrzymujemy
jest równoramienny. Stosując do niego twierdzenie Ptolemeusza, otrzymujemy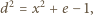
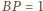 oraz
oraz 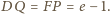 Łącząc uzyskane równości, mamy
Łącząc uzyskane równości, mamy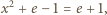
 i
i 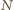 środki ramion
środki ramion 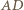 i
i 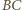 trapezu, a przez
trapezu, a przez 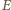 punkt przecięcia jego przekątnych. Wówczas na mocy nierówności trójkąta
punkt przecięcia jego przekątnych. Wówczas na mocy nierówności trójkąta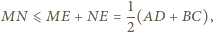
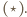 Jednocześnie w trapezie
Jednocześnie w trapezie 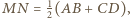 co kończy dowód.
co kończy dowód.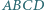 wybrano taki punkt
wybrano taki punkt 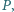 że
że 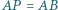 oraz
oraz 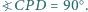 Wykaż, że
Wykaż, że 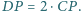
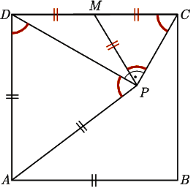
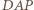 jest równoramienny, gdyż
jest równoramienny, gdyż 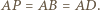 Ponadto
Ponadto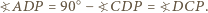
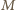 będzie środkiem boku
będzie środkiem boku 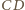 trójkąta prostokątnego
trójkąta prostokątnego 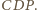 Wówczas trójkąt
Wówczas trójkąt 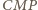 jest równoramienny i na mocy powyższej równości kątów podobny do trójkąta
jest równoramienny i na mocy powyższej równości kątów podobny do trójkąta 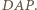 Stąd
Stąd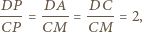
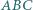 środkowe poprowadzone z wierzchołków
środkowe poprowadzone z wierzchołków 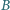 i
i 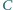 są prostopadłe oraz
są prostopadłe oraz 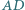 jest wysokością. Wykaż, że
jest wysokością. Wykaż, że 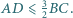
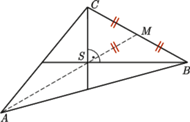
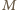 będzie środkiem boku
będzie środkiem boku 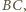 a
a 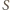 - środkiem ciężkości trójkąta
- środkiem ciężkości trójkąta 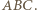 Wówczas
Wówczas 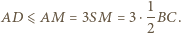
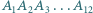 o środku
o środku 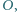 przy czym
przy czym 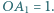 Punkt
Punkt 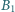 jest rzutem
jest rzutem 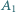 na odcinek
na odcinek 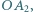 punkt
punkt 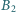 jest rzutem
jest rzutem 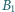 na
na 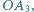 punkt
punkt 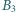 jest rzutem
jest rzutem 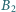 na
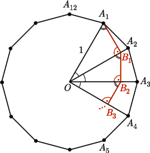
na 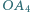 itd. Wyznacz długość łamanej
itd. Wyznacz długość łamanej 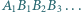

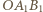 oraz
oraz 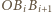 mają kąty po
mają kąty po 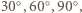 gdyż każdy z nich z założenia jest prostokątny i ma kąt
gdyż każdy z nich z założenia jest prostokątny i ma kąt 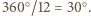 Można wobec tego ułożyć je w sposób przedstawiony na rysunku. Kąt pomiędzy sąsiadującymi teraz odcinkami rozważanej łamanej jest wówczas równy
Można wobec tego ułożyć je w sposób przedstawiony na rysunku. Kąt pomiędzy sąsiadującymi teraz odcinkami rozważanej łamanej jest wówczas równy 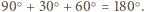
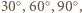 przy czym jedna jego przyprostokątna ma długość 1, a suma pozostałych dwóch boków to szukana długość łamanej. Jest ona wobec tego równa
przy czym jedna jego przyprostokątna ma długość 1, a suma pozostałych dwóch boków to szukana długość łamanej. Jest ona wobec tego równa 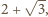 gdyż trójkąt ten jest połową trójkąta równobocznego o boku 2.
gdyż trójkąt ten jest połową trójkąta równobocznego o boku 2.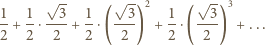
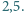 Wykaż, że obwód tego czworokąta jest większy od 7.
Wykaż, że obwód tego czworokąta jest większy od 7.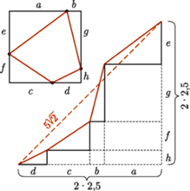
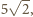 co z kolei jest większe od 7.
co z kolei jest większe od 7.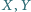 są środkami odpowiednio boków
są środkami odpowiednio boków 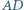 i
i 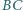 czworokąta wypukłego
czworokąta wypukłego 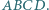 Udowodnij, że
Udowodnij, że 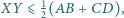 przy czym równość zachodzi wtedy i tylko wtedy, gdy
przy czym równość zachodzi wtedy i tylko wtedy, gdy 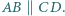
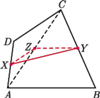
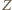 będzie środkiem przekątnej
będzie środkiem przekątnej 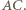 Wówczas
Wówczas 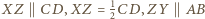 oraz
oraz 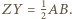 Stąd na mocy nierówności trójkąta dla punktów
Stąd na mocy nierówności trójkąta dla punktów 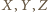 mamy
mamy 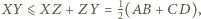 przy czym równość zachodzi wtedy i tylko wtedy, gdy
przy czym równość zachodzi wtedy i tylko wtedy, gdy 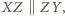 czyli gdy
czyli gdy 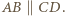
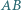 i
i 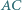 trójkąta
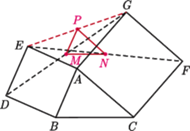
trójkąta 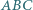 zbudowano, po jego zewnętrznej stronie, kwadraty
zbudowano, po jego zewnętrznej stronie, kwadraty 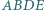 i
i 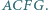 Punkty
Punkty 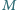 i
i 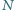 są odpowiednio środkami odcinków
są odpowiednio środkami odcinków 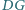 i
i 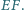 Wyznacz możliwe wartości wyrażenia
Wyznacz możliwe wartości wyrażenia 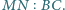
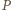 będzie środkiem odcinka
będzie środkiem odcinka 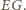 Wówczas
Wówczas 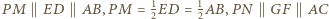 oraz
oraz 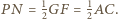 Wobec tego trójkąty
Wobec tego trójkąty 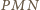 i
i 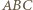 są podobne w skali
są podobne w skali 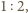 a więc
a więc 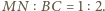
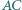 i
i 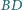 czworokąta wypukłego
czworokąta wypukłego 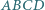 są równej długości. Punkty
są równej długości. Punkty 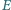 i
i 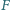 są odpowiednio środkami boków
są odpowiednio środkami boków 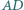 i
i 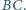 Udowodnij, że prosta
Udowodnij, że prosta 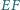 tworzy równe kąty z przekątnymi
tworzy równe kąty z przekątnymi 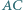 i
i 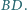

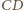 przez
przez 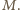 Wówczas
Wówczas 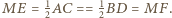 Wobec tego trójkąt
Wobec tego trójkąt 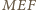 jest równoramienny i podstawa
jest równoramienny i podstawa 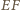 tworzy równe kąty z bokami
tworzy równe kąty z bokami 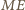 i
i 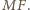 Jednocześnie
Jednocześnie 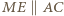 oraz
oraz 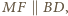 co kończy dowód.
co kończy dowód.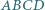 nie jest równoległobokiem oraz
nie jest równoległobokiem oraz 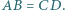 Punkty
Punkty 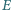 i
i 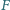 są odpowiednio środkami przekątnych
są odpowiednio środkami przekątnych 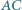 i
i 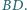 Wykaż, że rzuty prostopadłe odcinków
Wykaż, że rzuty prostopadłe odcinków 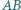 i
i 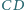 na prostą
na prostą 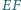 są równej długości.
są równej długości.
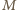 będzie środkiem boku
będzie środkiem boku 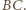 Wówczas
Wówczas 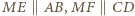 oraz
oraz 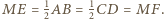 Wobec tego trójkąt
Wobec tego trójkąt 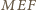 jest równoramienny (
jest równoramienny ( 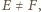 gdyż
gdyż 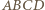 nie jest równoległobokiem). Stąd rzut
nie jest równoległobokiem). Stąd rzut 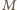 na prostą
na prostą 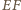 jest środkiem podstawy
jest środkiem podstawy 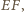 a więc rzuty boków
a więc rzuty boków 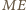 i
i 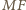 na prostą
na prostą 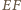 są równej długości jako połówki podstawy. Wobec tego również dwukrotnie od nich dłuższe rzuty odcinków
są równej długości jako połówki podstawy. Wobec tego również dwukrotnie od nich dłuższe rzuty odcinków 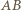 i
i 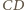 są równej długości.
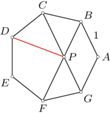
są równej długości.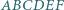 o polu 1 punkty
o polu 1 punkty  są środkami odpowiednio przekątnych
są środkami odpowiednio przekątnych  i tworzą sześciokąt wypukły
i tworzą sześciokąt wypukły  Wyznacz jego pole.
Wyznacz jego pole.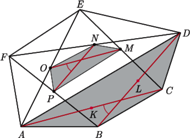
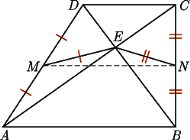
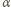 oznacza miarę nie większego z kątów pomiędzy przekątnymi
oznacza miarę nie większego z kątów pomiędzy przekątnymi 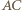 i
i 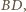 wówczas
wówczas ![|[ABCD] = 12AC⋅ BD⋅sinα .](/math/temat/matematyka/geometria/planimetria/zadania/2017/04/29/zm-17_05-deltoid-5/4x-9b80fedd92e33e6d528df9e7b09e1c2f4c115de4-im-66,57,43-FF,FF,FF.gif) Jednocześnie
Jednocześnie 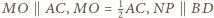 oraz
oraz 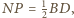 zatem kąt pomiędzy odcinkami
zatem kąt pomiędzy odcinkami 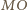 i
i 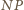 także jest równy
także jest równy 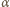 oraz
oraz![[MNOP] = 1MO⋅ NP ⋅sinα = 1CA⋅BD⋅sin α = 1[ABCD]. 2 8 4](/math/temat/matematyka/geometria/planimetria/zadania/2017/04/29/zm-17_05-deltoid-5/10x-9b80fedd92e33e6d528df9e7b09e1c2f4c115de4-dm-66,57,43-FF,FF,FF.gif)
![|[PKLM] = 14[DEFA],](/math/temat/matematyka/geometria/planimetria/zadania/2017/04/29/zm-17_05-deltoid-5/11x-9b80fedd92e33e6d528df9e7b09e1c2f4c115de4-im-66,57,43-FF,FF,FF.gif) stąd
stąd ![[KLMNOP] = 14[ABCDEF] = 14.](/math/temat/matematyka/geometria/planimetria/zadania/2017/04/29/zm-17_05-deltoid-5/12x-9b80fedd92e33e6d528df9e7b09e1c2f4c115de4-im-66,57,43-FF,FF,FF.gif)
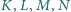 będą środkami kolejnych boków czworokąta
będą środkami kolejnych boków czworokąta 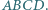 Wykaż, że
Wykaż, że 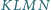 jest równoległobokiem, że
jest równoległobokiem, że 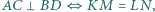 że
że 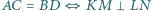 oraz wyznacz stosunek pól
oraz wyznacz stosunek pól ![N] [ABCD]. [KLM](/math/temat/matematyka/geometria/planimetria/zadania/2017/04/29/zm-17_05-deltoid-6/6x-476c50773c7ee85da9c32be7747c5f72357fd03b-im-2C,6B,73-FF,FF,FF.gif)
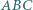 o bokach
o bokach 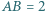 oraz
oraz 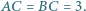 Punkt
Punkt 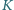 jest środkiem boku
jest środkiem boku 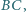 punkt
punkt 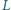 leży na boku
leży na boku 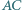 oraz
oraz 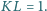 Wyznacz długość odcinka
Wyznacz długość odcinka 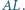
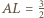 to tylko jedna z możliwości.
to tylko jedna z możliwości.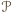 oznaczmy przez
oznaczmy przez 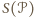 lekko zmodyfikowaną sumę miar kątów wewnętrznych wielokąta
lekko zmodyfikowaną sumę miar kątów wewnętrznych wielokąta 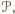 mianowicie taką, w której zamiast kątów wklęsłych występują kąty dopełniające je do pełnych ze znakiem "
mianowicie taką, w której zamiast kątów wklęsłych występują kąty dopełniające je do pełnych ze znakiem "  ". Jeżeli więc
". Jeżeli więc 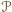 jest
jest 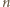 -kątem o dokładnie
-kątem o dokładnie 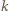 wklęsłych kątach wewnętrznych, to definiujemy
wklęsłych kątach wewnętrznych, to definiujemy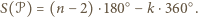
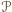 jest podzielony odcinkami na wielokąty
jest podzielony odcinkami na wielokąty 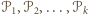 o rozłącznych wnętrzach. Wierzchołkami podziału nazwijmy te wierzchołki wielokątów
o rozłącznych wnętrzach. Wierzchołkami podziału nazwijmy te wierzchołki wielokątów 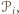 które nie są wierzchołkami wielokąta
które nie są wierzchołkami wielokąta 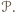 Wówczas
Wówczas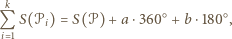
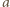 jest liczbą wierzchołków podziału wokół których znajdują się tylko kąty wypukłe wielokątów
jest liczbą wierzchołków podziału wokół których znajdują się tylko kąty wypukłe wielokątów 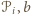 zaś jest liczbą wierzchołków podziału leżących na bokach wielokąta
zaś jest liczbą wierzchołków podziału leżących na bokach wielokąta 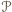 (w przypadku wierzchołków podziału, będących wierzchołkami pewnych kątów wklęsłych wielokątów
(w przypadku wierzchołków podziału, będących wierzchołkami pewnych kątów wklęsłych wielokątów 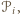 "wychodzimy na zero", zgodnie z definicją
"wychodzimy na zero", zgodnie z definicją 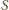 ).
).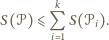
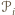 były czworokątami wklęsłymi, to
były czworokątami wklęsłymi, to 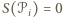 dla każdego
dla każdego 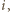 wobec czego
wobec czego