Zadanie ZM-1295
o zadaniu...
- Publikacja w Delcie:
- Publikacja elektroniczna:
Dany jest trapez
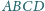 o podstawach
o podstawach
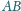 i
i
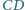 ,
w którym
,
w którym
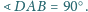 Proste
Proste
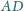 i
i
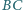 przecinają się
w punkcie
przecinają się
w punkcie
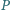 . Punkty
. Punkty
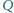 i
i
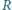 są rzutami prostokątnymi
odpowiednio punktów
są rzutami prostokątnymi
odpowiednio punktów
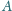 i
i
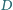 na proste
na proste
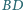 i
i
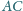 .
Dowieść, że punkty
.
Dowieść, że punkty
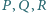 leżą na jednej prostej.
leżą na jednej prostej.
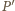 punkt przecięcia prostych
punkt przecięcia prostych
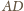 i
i
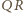 .
Należy dowieść, że
.
Należy dowieść, że
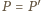 . Rozpatrzmy okrąg o średnicy
. Rozpatrzmy okrąg o średnicy
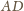 .
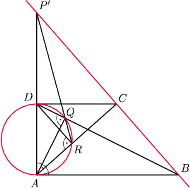
Okrąg ten przechodzi przez punkty Q i R. Korzystając zatem z twierdzenia
Pascala dla „sześciokąta” AAQRDD, wnioskujemy, że punkty B, C oraz P’ leżą
na jednej prostej. Stąd P = P’.
.
Okrąg ten przechodzi przez punkty Q i R. Korzystając zatem z twierdzenia
Pascala dla „sześciokąta” AAQRDD, wnioskujemy, że punkty B, C oraz P’ leżą
na jednej prostej. Stąd P = P’.
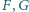 leżą wewnątrz trójkąta ostrokątnego
leżą wewnątrz trójkąta ostrokątnego
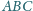 ,
przy czym
,
przy czym
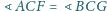 i
i
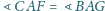 . Punkty
. Punkty
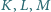 są rzutami prostokątnymi punktu
są rzutami prostokątnymi punktu
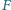 odpowiednio na
boki
odpowiednio na
boki
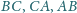 . Wykaż, że kąt
. Wykaż, że kąt
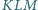 jest prosty wtedy
i tylko wtedy, gdy punkt
jest prosty wtedy
i tylko wtedy, gdy punkt
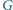 jest punktem przecięcia wysokości
trójkąta
jest punktem przecięcia wysokości
trójkąta
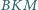 .
.
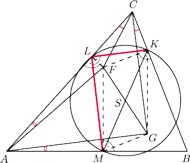
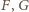 są ogniskami pewnej elipsy wpisanej
w trójkąt
są ogniskami pewnej elipsy wpisanej
w trójkąt
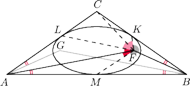
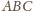 (rysunek). Na mocy wskazówki punkty
(rysunek). Na mocy wskazówki punkty
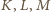 leżą na okręgu o środku w środku
leżą na okręgu o środku w środku
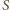 odcinka
odcinka
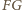 . Kąt
. Kąt
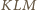 jest prosty
jest prosty
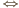
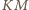 jest średnicą tego okręgu
jest średnicą tego okręgu
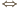
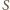 jest środkiem
jest środkiem
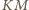
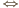
 jest
równoległobokiem
jest
równoległobokiem
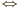
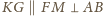 oraz
oraz
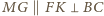
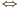
 jest punktem przecięcia wysokości trójkąta
jest punktem przecięcia wysokości trójkąta
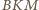 .
.
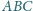 , w którym
, w którym
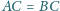 . Punkt
. Punkt
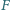 leży
wewnątrz trójkąta
leży
wewnątrz trójkąta
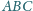 , przy czym
, przy czym
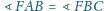 . Punkt
. Punkt
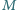 jest środkiem boku
jest środkiem boku
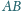 . Udowodnij, że
. Udowodnij, że
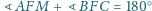 .
.
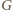 będzie obrazem
będzie obrazem
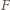 w symetrii względem prostej
w symetrii względem prostej
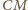 .
Wtedy
.
Wtedy
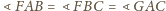 oraz
oraz
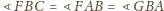 .
Z ćwiczenia (c) istnieje więc elipsa o ogniskach
.
Z ćwiczenia (c) istnieje więc elipsa o ogniskach
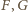 , wpisana w trójkąt
, wpisana w trójkąt
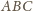 . Jest ona styczna do boku
. Jest ona styczna do boku
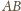 w punkcie
w punkcie
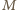 i do boków
i do boków
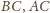 odpowiednio w
odpowiednio w
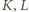 . Z Faktu,
. Z Faktu,
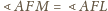 ,
,
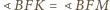 ,
,
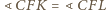 . Suma tych sześciu kątów daje
kąt pełny
. Suma tych sześciu kątów daje
kąt pełny
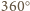 , zatem
, zatem
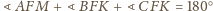 , co
kończy dowód.
, co
kończy dowód.
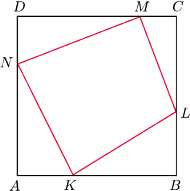
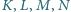 leżą odpowiednio na bokach
leżą odpowiednio na bokach
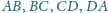 kwadratu
kwadratu
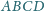 o boku
o boku
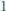 . Wyznaczyć najmniejszy możliwy
obwód czworokąta
. Wyznaczyć najmniejszy możliwy
obwód czworokąta
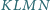 .
.
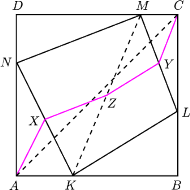
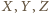 odpowiednio środki odcinków
odpowiednio środki odcinków
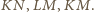 Ponieważ trójkąty
Ponieważ trójkąty
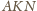 oraz
oraz
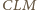 są
prostokątne, więc
są
prostokątne, więc


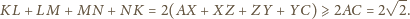
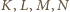 jako środki odcinków
jako środki odcinków
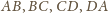 ,
otrzymujemy kwadrat
,
otrzymujemy kwadrat
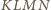 o obwodzie
o obwodzie
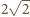 .
.
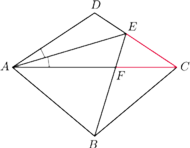
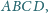 w którym
w którym
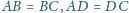 oraz
oraz
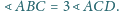 Dwusieczna kąta
Dwusieczna kąta
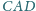 przecina
bok
przecina
bok
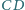 w punkcie
w punkcie
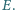 Odcinki
Odcinki
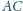 i
i
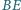 przecinają się w punkcie
przecinają się w punkcie
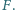 Wykazać, że trójkąt
Wykazać, że trójkąt
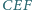 jest
równoramienny.
jest
równoramienny.
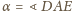 (rysunek). Wtedy
(rysunek). Wtedy
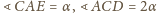 oraz
oraz
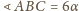 . Ponadto
. Ponadto
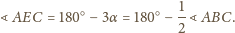
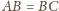 wynika, że okrąg o środku
wynika, że okrąg o środku
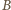 i promieniu
i promieniu
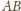 przechodzi przez punkty
przechodzi przez punkty
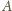 ,
,
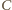 oraz
oraz
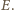 Wobec tego
Wobec tego
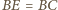 , skąd otrzymujemy
, skąd otrzymujemy
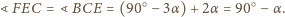
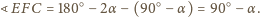
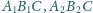 i
i
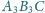 są zorientowane
antyzegarowo. Punkty
są zorientowane
antyzegarowo. Punkty
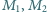 i
i
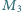 są środkami odpowiednio
odcinków
są środkami odpowiednio
odcinków
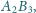
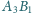 i
i
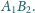 Udowodnij, że trójkąt
Udowodnij, że trójkąt
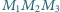 jest równoboczny i zorientowany zegarowo.
jest równoboczny i zorientowany zegarowo.
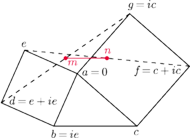
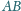 i
i
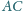 trójkąta
trójkąta
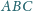 zbudowano,
po jego zewnętrznej stronie, kwadraty
zbudowano,
po jego zewnętrznej stronie, kwadraty
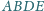 i
i
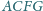 . Punkty
. Punkty
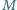 i
i
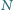 są odpowiednio środkami odcinków
są odpowiednio środkami odcinków
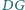 i
i
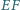 . Wyznacz możliwe wartości wyrażenia
. Wyznacz możliwe wartości wyrażenia
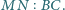
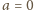 . Z faktu 2 mamy
. Z faktu 2 mamy
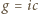 oraz
oraz
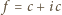 ,
a także
,
a także
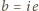 oraz
oraz
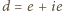 . Z faktu 1 wyznaczamy
. Z faktu 1 wyznaczamy
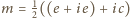 oraz
oraz
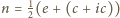 , a także
, a także
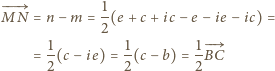
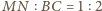 .
.