Środek ciężkości»Zadanie 2
o zadaniu...
- Zadanie pochodzi z artykułu Środek ciężkości
- Publikacja w Delcie: listopad 2011
- Publikacja elektroniczna: 01-11-2011
- Artykuł źródłowy w wersji do druku [application/pdf]: (83 KB)
Wykaż, że środkowe trójkąta przecinają się w środku ciężkości jego wierzchołków.
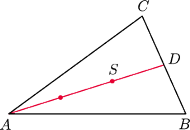
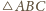 równe masy
równe masy
 Wtedy
Wtedy
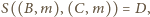 gdzie
gdzie
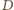 to środek
to środek
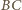 . Środek
ciężkości trójkąta
. Środek
ciężkości trójkąta
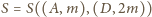 leży na środkowej
leży na środkowej
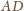 ; analogicznie leży na pozostałych środkowych. Ponadto
; analogicznie leży na pozostałych środkowych. Ponadto
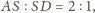 czyli środkowe dzielą się w stosunku
czyli środkowe dzielą się w stosunku
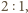 licząc
od wierzchołka.
licząc
od wierzchołka.
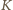 na boku
na boku
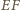 trójkąta
trójkąta
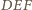 spełnia
spełnia
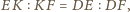 to jest
spodkiem dwusiecznej
to jest
spodkiem dwusiecznej
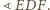
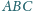 umieszczono masy
odpowiednio
umieszczono masy
odpowiednio
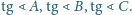 Wykaż, że ich środkiem
ciężkości jest ortocentrum
Wykaż, że ich środkiem
ciężkości jest ortocentrum
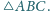
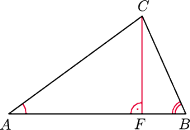
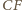 jest wysokością
jest wysokością
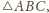 to
to
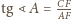 i
i
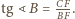 Stąd
Stąd
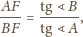
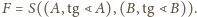 Szukany środek ciężkości
leży więc na
Szukany środek ciężkości
leży więc na
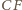 i analogicznie na wysokościach z
i analogicznie na wysokościach z
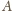 i z
i z
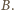
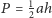
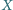 leży wewnątrz sześciokąta wypukłego
leży wewnątrz sześciokąta wypukłego
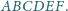 Punkty
Punkty
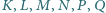 są odpowiednio
środkami boków
są odpowiednio
środkami boków
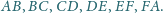 Wykaż, że
Wykaż, że
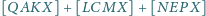 nie zależy od wyboru punktu
nie zależy od wyboru punktu
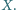
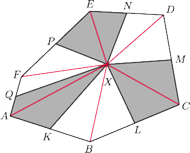
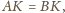 to
to
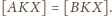 Podobnie
Podobnie
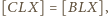
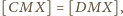
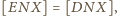
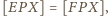
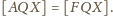 Dodając
stronami, uzyskujemy
Dodając
stronami, uzyskujemy
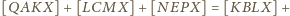
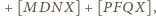 czyli
czyli
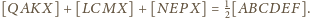
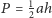
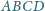 o polu 1. Punkt
o polu 1. Punkt
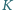 jest
symetryczny do punktu
jest
symetryczny do punktu
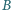 względem punktu
względem punktu
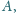 punkt
punkt
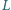 jest
symetryczny do punktu
jest
symetryczny do punktu
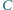 względem punktu
względem punktu
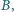 punkt
punkt
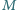 jest symetryczny do punktu
jest symetryczny do punktu
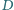 względem punktu
względem punktu
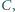 punkt
punkt
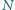 jest symetryczny do punktu
jest symetryczny do punktu
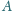 względem
punktu
względem
punktu
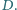 Oblicz
Oblicz
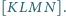
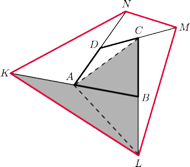
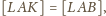 bo trójkąty te mają równe
podstawy
bo trójkąty te mają równe
podstawy
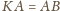 i wspólną wysokość z
i wspólną wysokość z
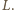 Ponadto
Ponadto
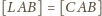 (ponieważ
(ponieważ
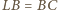 ). Analogicznie
). Analogicznie
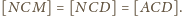 Stąd
Stąd
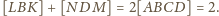 Podobnie
Podobnie
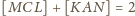 i ostatecznie
i ostatecznie
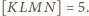
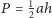
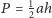
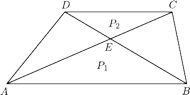
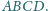 Punkty
Punkty
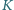 i
i
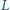 należą
do boku
należą
do boku
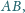 przy czym
przy czym
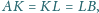 a punkty
a punkty
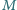 i
i
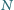 należą do boku
należą do boku
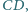 przy czym
przy czym
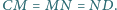 Wykaż,
że
Wykaż,
że
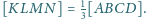
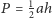
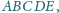 w którym pola trójkątów
w którym pola trójkątów
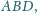
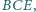
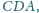
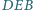 i
i
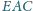 są równe.
Udowodnij, że każda przekątna tego pięciokąta jest równoległa do pewnego
jego boku.
są równe.
Udowodnij, że każda przekątna tego pięciokąta jest równoległa do pewnego
jego boku.
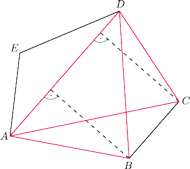
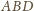 i
i
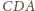 mają wspólną podstawę
mają wspólną podstawę
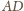 i równe
pola, więc też równe wysokości. Punkty
i równe
pola, więc też równe wysokości. Punkty
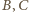 są po tej samej stronie
prostej
są po tej samej stronie
prostej
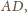 stąd
stąd
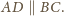 Dla pozostałych przekątnych dowód
jest analogiczny.
Dla pozostałych przekątnych dowód
jest analogiczny.
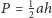
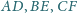 sześciokąta wypukłego
sześciokąta wypukłego
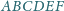 dzieli go na dwa czworokąty o równych polach. Wykaż, że
trójkąty
dzieli go na dwa czworokąty o równych polach. Wykaż, że
trójkąty
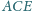 i
i
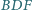 są podobne.
są podobne.
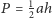
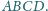 Punkty
Punkty
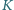 i
i
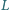 należą
odpowiednio do odcinków
należą
odpowiednio do odcinków
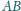 i
i
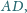 przy czym czworokąt
przy czym czworokąt
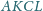 jest równoległobokiem. Odcinki
jest równoległobokiem. Odcinki
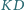 i
i
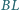 przecinają
się w punkcie
przecinają
się w punkcie
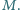 Wykaż, że
Wykaż, że
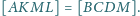
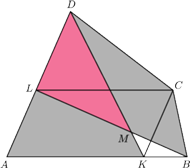
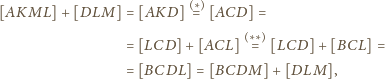
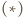 wynika z równoległości
wynika z równoległości
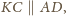 a
a
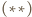 z
z
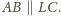
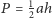
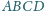 przecinają się w punkcie
przecinają się w punkcie
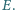 Wyznacz
Wyznacz
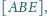 jeśli
jeśli
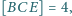
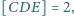
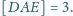
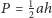
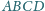 o podstawach
o podstawach
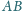 i
i
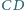 przecinają się
w punkcie
przecinają się
w punkcie
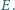 Dane są
Dane są
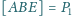 i
i
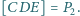 Wyznacz
Wyznacz
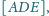
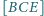 oraz
oraz
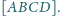
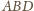 i
i
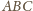 mają wspólną podstawę i równe
wysokości, więc też równe pola. Stąd
mają wspólną podstawę i równe
wysokości, więc też równe pola. Stąd
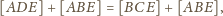
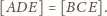
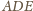 i
i
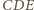 mają wspólną wysokość z
mają wspólną wysokość z
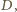 więc
więc
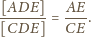
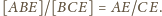 Stąd
Stąd
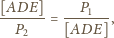
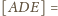
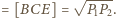 Wobec tego
Wobec tego
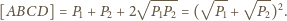
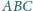 jest styczny do boków
jest styczny do boków
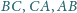 odpowiednio w punktach
odpowiednio w punktach
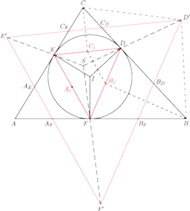
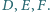 Prowadzimy trzy
proste: przez środki odcinków
Prowadzimy trzy
proste: przez środki odcinków
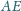 i
i
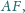 przez środki
odcinków
przez środki
odcinków
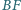 i
i
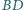 oraz przez środki odcinków
oraz przez środki odcinków
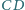 i
i
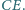 Wykazać, że środek okręgu opisanego na trójkącie wyznaczonym
przez te trzy proste pokrywa się ze środkiem okręgu opisanego na trójkącie
Wykazać, że środek okręgu opisanego na trójkącie wyznaczonym
przez te trzy proste pokrywa się ze środkiem okręgu opisanego na trójkącie
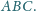
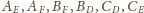 będą środkami odcinków
będą środkami odcinków
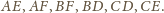 Z twierdzenia Talesa wynika, że
Z twierdzenia Talesa wynika, że
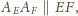
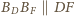 i
i
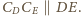 Przez
Przez
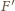 oznaczamy punkt wspólny prostych
oznaczamy punkt wspólny prostych
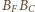 i
i
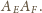 Analogicznie definiujemy punkty
Analogicznie definiujemy punkty
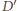 i
i
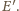 Boki
trójkątów
Boki
trójkątów
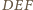 i
i
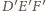 są odpowiednio równoległe, więc
punkt
są odpowiednio równoległe, więc
punkt
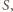 w którym przecinają się proste
w którym przecinają się proste
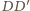 i
i
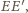 jest
środkiem jednokładności w skali
jest
środkiem jednokładności w skali
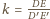 przekształcającej trójkąt
przekształcającej trójkąt
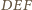 na trójkąt
na trójkąt
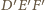 (
(
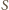 leży też na prostej
leży też na prostej
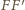 ).
).
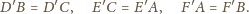
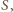 w skali
w skali
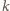 przekształca okrąg
przekształca okrąg
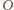 opisany na trójkącie
opisany na trójkącie
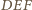 na okrąg
na okrąg
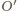 opisany na trójkącie
opisany na trójkącie
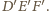 Środek okręgu
Środek okręgu
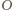 leży na prostopadłych do prostych
leży na prostopadłych do prostych
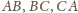 przechodzących
przez wierzchołki
przechodzących
przez wierzchołki
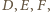 więc środek okręgu
więc środek okręgu
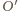 leży na
prostopadłych do prostych
leży na
prostopadłych do prostych
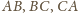 przechodzących przez wierzchołki
przechodzących przez wierzchołki
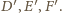 Na mocy lematu (dowód w artykule) te prostopadłe są
symetralnymi boków trójkąta
Na mocy lematu (dowód w artykule) te prostopadłe są
symetralnymi boków trójkąta
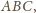 więc ich punkt wspólny to
środek okręgu opisanego na trójkącie
więc ich punkt wspólny to
środek okręgu opisanego na trójkącie
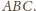
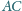 i
i
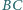 trójkąta równoramiennego
trójkąta równoramiennego
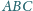 mają
długość 1. Dla jakiej podstawy
mają
długość 1. Dla jakiej podstawy
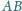 pole tego trójkąta jest
maksymalne?
pole tego trójkąta jest
maksymalne?
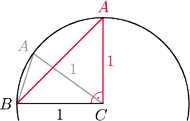
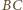 było podstawą. Wtedy wierzchołek
było podstawą. Wtedy wierzchołek
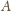 leży na okręgu o środku
leży na okręgu o środku
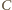 i promieniu 1. Pole trójkąta jest
maksymalne, gdy wysokość z
i promieniu 1. Pole trójkąta jest
maksymalne, gdy wysokość z
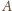 jest maksymalna (bo podstawa
jest maksymalna (bo podstawa
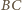 ma ustaloną długość 1), czyli gdy wysokość ta jest równa 1.
Zachodzi to dla
ma ustaloną długość 1), czyli gdy wysokość ta jest równa 1.
Zachodzi to dla
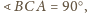 czyli dla
czyli dla
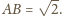
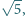
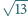 i
i
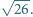
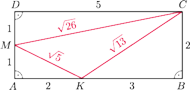
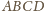 o bokach
o bokach
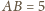 i
i
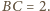 Niech
punkt
Niech
punkt
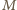 będzie środkiem boku
będzie środkiem boku
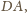 a punkt
a punkt
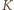 niech należy
do boku
niech należy
do boku
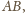 przy czym
przy czym
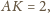
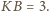 Wtedy z twierdzenia
Pitagorasa
Wtedy z twierdzenia
Pitagorasa
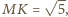
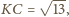
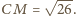 Należy
obliczyć pole trójkąta
Należy
obliczyć pole trójkąta
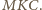 Jest ono równe
Jest ono równe
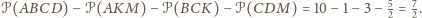
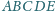 kąty przy wierzchołkach
kąty przy wierzchołkach
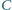 i
i
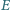 są proste. Oblicz
są proste. Oblicz
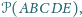 jeśli
jeśli
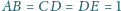 oraz
oraz
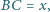
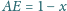 dla
dla
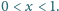
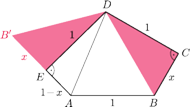
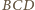 obok trójkąta
obok trójkąta
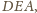 jak na rysunku
(
jak na rysunku
(
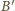 oznacza odpowiednik wierzchołka
oznacza odpowiednik wierzchołka
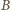 ). Wtedy w trójkącie
). Wtedy w trójkącie
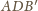 podstawa
podstawa
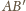 ma długość
ma długość
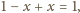 wysokość
wysokość
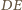 jest równa 1, więc pole jest równe
jest równa 1, więc pole jest równe
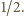 Pozostałą
częścią pięciokąta jest trójkąt
Pozostałą
częścią pięciokąta jest trójkąt
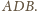 Przystaje on do trójkąta
Przystaje on do trójkąta
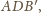 ponieważ
ponieważ
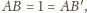
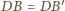 oraz bok
oraz bok
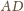 jest wspólny. Stąd
jest wspólny. Stąd
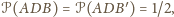 więc pole
pięciokąta równe jest 1.
więc pole
pięciokąta równe jest 1.
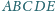 , w którym pola trójkątów
, w którym pola trójkątów
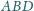 ,
,
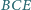 ,
,
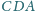 ,
,
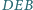 i
i
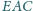 są równe.
Wykaż, że każda przekątna tego pięciokąta jest równoległa do pewnego
jego boku.
są równe.
Wykaż, że każda przekątna tego pięciokąta jest równoległa do pewnego
jego boku.
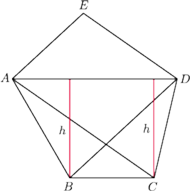
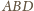 i
i
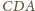 mają równe pola oraz wspólny
bok
mają równe pola oraz wspólny
bok
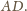 Wobec tego wysokości tych trójkątów poprowadzone do
boku
Wobec tego wysokości tych trójkątów poprowadzone do
boku
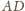 są równe. Ponadto punkty
są równe. Ponadto punkty
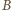 i
i
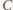 leżą po
tej samej stronie prostej
leżą po
tej samej stronie prostej
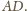 Stąd wniosek, że przekątna
Stąd wniosek, że przekątna
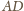 jest
równoległa do boku
jest
równoległa do boku
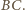 Analogicznie dowodzimy, że pozostałe cztery
przekątne pięciokąta
Analogicznie dowodzimy, że pozostałe cztery
przekątne pięciokąta
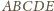 są równoległe do odpowiednich jego
boków
są równoległe do odpowiednich jego
boków
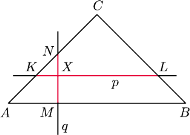
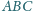 o kącie prostym
przy wierzchołku
o kącie prostym
przy wierzchołku
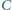 . Znaleźć zbiór takich punktów
. Znaleźć zbiór takich punktów
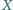 z wnętrza trójkąta
z wnętrza trójkąta
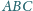 , że jeśli prosta
, że jeśli prosta
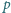 równoległa do
podstawy
równoległa do
podstawy
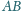 przechodząca przez punkt
przechodząca przez punkt
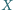 przecina ramiona
przecina ramiona
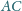 i
i
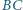 w punktach
w punktach
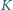 i
i
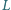 , zaś
, zaś
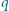 jest prostą
prostopadłą do
jest prostą
prostopadłą do
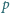 przechodzącą przez
przechodzącą przez
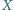 , przecinającą podstawę
, przecinającą podstawę
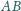 trójkąta w punkcie
trójkąta w punkcie
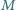 , a ramię w punkcie
, a ramię w punkcie
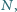 to
to
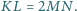
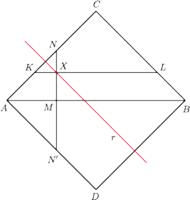
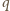 przecina ramię
przecina ramię
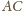 . Rozszerzmy nasz
trójkąt do kwadratu
. Rozszerzmy nasz
trójkąt do kwadratu
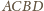 .
.
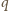 z nowo dorysowanym bokiem kwadratu
oznaczmy przez
z nowo dorysowanym bokiem kwadratu
oznaczmy przez
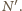 Szukamy takich punktów
Szukamy takich punktów
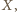 że
że
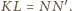 Równoważnie takich, że odcinki
Równoważnie takich, że odcinki
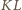 i
i
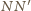 są symetryczne względem prostej
są symetryczne względem prostej
 prostopadłej do
prostopadłej do
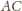 przechodzącej przez
przechodzącej przez
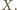 To zachodzi wtedy i tylko wtedy, gdy
trójkąty
To zachodzi wtedy i tylko wtedy, gdy
trójkąty
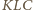 i
i
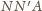 są symetryczne względem tej prostej, co jest
z kolei równoważne temu, że punkty
są symetryczne względem tej prostej, co jest
z kolei równoważne temu, że punkty
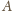 i
i
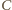 są symetryczne
względem
są symetryczne
względem
 (bo punkty
(bo punkty
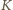 i
i
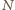 zostały skonstruowane tak,
że są symetryczne względem
zostały skonstruowane tak,
że są symetryczne względem
 ).
).
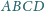 i
i
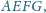 tak samo zorientowane, mają wspólny
tylko punkt
tak samo zorientowane, mają wspólny
tylko punkt
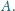 Wykaż, że
Wykaż, że
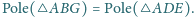
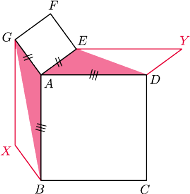
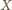 będzie czwartym wierzchołkiem równoległoboku
będzie czwartym wierzchołkiem równoległoboku
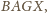 a
a
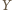 – czwartym wierzchołkiem równoległoboku
– czwartym wierzchołkiem równoległoboku
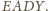 Równoległoboki te są przystające, ponieważ
Równoległoboki te są przystające, ponieważ
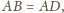
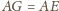 oraz
oraz
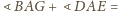
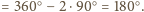 Stąd
Stąd
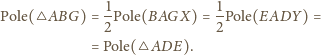
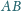 i
i
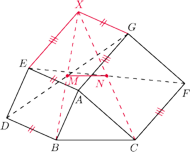
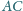 trójkąta
trójkąta
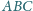 zbudowano, po jego
zewnętrznej stronie, kwadraty
zbudowano, po jego
zewnętrznej stronie, kwadraty
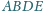 i
i
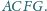 Punkty
Punkty
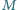 i
i
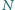 są odpowiednio środkami odcinków
są odpowiednio środkami odcinków
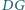 i
i
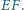 Wyznacz możliwe wartości wyrażenia
Wyznacz możliwe wartości wyrażenia
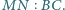
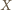 będzie czwartym wierzchołkiem równoległoboku
będzie czwartym wierzchołkiem równoległoboku
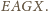 Wtedy
Wtedy
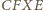 także jest równoległobokiem (bo
także jest równoległobokiem (bo
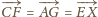 ). Wobec tego punkt
). Wobec tego punkt
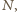 jako środek jego przekątnej
jako środek jego przekątnej
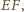 jest też środkiem drugiej przekątnej
jest też środkiem drugiej przekątnej
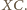 Analogicznie
Analogicznie
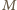 jest środkiem
jest środkiem
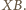 Stąd i z twierdzenia Talesa uzyskujemy
Stąd i z twierdzenia Talesa uzyskujemy
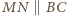 oraz
oraz