Narysuj równoległobok!»Zadanie 3
o zadaniu...
- Zadanie pochodzi z artykułu Narysuj równoległobok!
- Publikacja w Delcie: maj 2011
- Publikacja elektroniczna: 04-05-2011
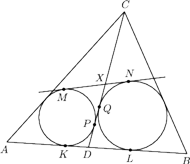
W trójkącie
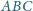 zachodzi równość
zachodzi równość
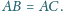 Punkt
Punkt
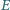 jest środkiem wysokości
jest środkiem wysokości
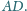 Punkt
Punkt
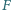 jest rzutem
prostokątnym punktu
jest rzutem
prostokątnym punktu
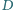 na prostą
na prostą
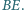 Udowodnij, że
Udowodnij, że
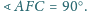
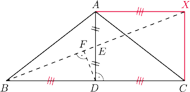
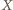 będzie czwartym wierzchołkiem prostokąta
będzie czwartym wierzchołkiem prostokąta
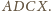 Wtedy
Wtedy
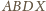 jest równoległobokiem o środku
jest równoległobokiem o środku
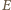 (bo
(bo
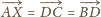 oraz
oraz
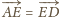 ), więc punkty
), więc punkty
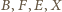 są
współliniowe. Odcinki
są
współliniowe. Odcinki
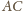 i
i
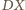 są średnicami okręgu opisanego
na prostokącie
są średnicami okręgu opisanego
na prostokącie
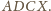 Ponadto
Ponadto
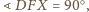 więc punkt
więc punkt
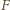 leży na tym okręgu. Stąd
leży na tym okręgu. Stąd
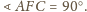
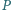 leży wewnątrz równoległoboku
leży wewnątrz równoległoboku
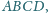 przy czym
przy czym
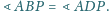 Wykaż, że
Wykaż, że
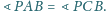
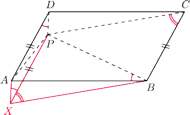
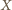 będzie czwartym wierzchołkiem równoległoboku
będzie czwartym wierzchołkiem równoległoboku
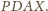 Wtedy
Wtedy
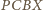 także jest równoległobokiem oraz
zachodzą równości
także jest równoległobokiem oraz
zachodzą równości
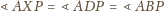
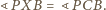
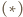 (uwzględniając wzajemne położenie odpowiednich
punktów) wynika, że punkty
(uwzględniając wzajemne położenie odpowiednich
punktów) wynika, że punkty
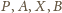 leżą na jednym okręgu. Wobec
tego
leżą na jednym okręgu. Wobec
tego
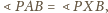 co razem z równością
co razem z równością
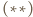 daje tezę.
daje tezę.
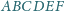 o polu 1 przeciwległe boki są
równe i równoległe. Wyznacz pole trójkąta
o polu 1 przeciwległe boki są
równe i równoległe. Wyznacz pole trójkąta
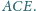
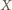 będzie czwartym wierzchołkiem równoległoboku
będzie czwartym wierzchołkiem równoległoboku
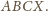 Wtedy
Wtedy
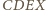 i
i
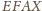 też są równoległobokami...
też są równoległobokami...
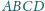 punkty
punkty
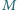 i
i
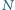 są środkami odpowiednio
ramion
są środkami odpowiednio
ramion
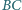 i
i
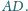 Wykaż, że
Wykaż, że
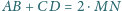 i że
i że


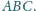 Wykaż, że z jego środkowych można
zbudować trójkąt.
Wykaż, że z jego środkowych można
zbudować trójkąt.
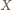 będzie czwartym wierzchołkiem równoległoboku
będzie czwartym wierzchołkiem równoległoboku
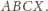
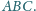 Punkty
Punkty
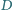 i
i
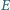 należą odpowiednio do boków
należą odpowiednio do boków
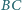 i
i
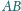 tego
trójkąta i
tego
trójkąta i
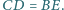 Punkt
Punkt
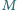 jest środkiem odcinka
jest środkiem odcinka
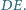 Udowodnij, że
Udowodnij, że
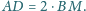
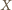 będzie czwartym wierzchołkiem równoległoboku
będzie czwartym wierzchołkiem równoległoboku
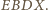
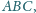 w którym
w którym
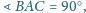 jest podstawą
ostrosłupa
jest podstawą
ostrosłupa
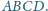 Ponadto zachodzą równości
Ponadto zachodzą równości
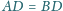 oraz
oraz
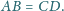 Wykaż, że
Wykaż, że
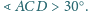
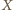 będzie czwartym wierzchołkiem prostokąta
będzie czwartym wierzchołkiem prostokąta
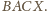
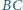 trójkąta
trójkąta
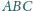 wybrano punkt
wybrano punkt
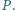 Punkty
Punkty
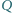 i
i
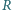 są środkami okręgów wpisanych w trójkąty
są środkami okręgów wpisanych w trójkąty
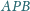 i
i
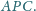 Punkt
Punkt
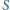 jest punktem styczności okręgu wpisanego w trójkąt
jest punktem styczności okręgu wpisanego w trójkąt
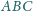 do boku
do boku
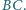 Wykazać, że punkty
Wykazać, że punkty
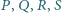 leżą na
jednym okręgu.
leżą na
jednym okręgu.
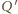 i
i
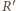 oznaczają rzuty punktów
oznaczają rzuty punktów
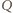 i
i
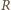 na
prostą
na
prostą
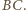 Z przyrównania odcinków stycznych do okręgu wpisanego
w trójkącie
Z przyrównania odcinków stycznych do okręgu wpisanego
w trójkącie
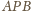 wynika równość
wynika równość
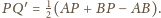 Podobnie mamy
Podobnie mamy
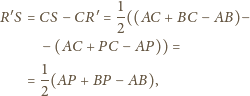
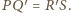 Stąd również
Stąd również
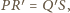 czyli
czyli
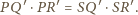
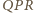 między dwusiecznymi kątów przyległych jest prosty,
więc trójkąty prostokątne
między dwusiecznymi kątów przyległych jest prosty,
więc trójkąty prostokątne
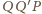 i
i
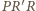 są podobne. W takim
razie
są podobne. W takim
razie
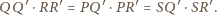
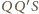 i
i
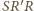 są podobne, więc kąt
są podobne, więc kąt
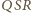 też
jest prosty. To oznacza, że punkty
też
jest prosty. To oznacza, że punkty
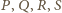 leżą na jednym
okręgu.
leżą na jednym
okręgu.
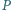 leżącego
wewnątrz trójkąta równobocznego
leżącego
wewnątrz trójkąta równobocznego
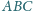 o boku
o boku
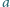 od jego
wierzchołków jest nie większa niż
od jego
wierzchołków jest nie większa niż
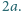
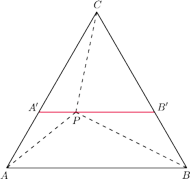
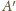 i
i
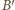 będą punktami przecięcia prostej równoległej
do
będą punktami przecięcia prostej równoległej
do
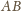 i przechodzącej przez punkt
i przechodzącej przez punkt
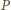 odpowiednio z bokami
odpowiednio z bokami
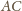 i
i
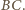 Trójkąt
Trójkąt
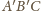 jest równoboczny i
jest równoboczny i
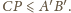 Ponadto stosując nierówność trójkąta, dostaniemy
Ponadto stosując nierówność trójkąta, dostaniemy
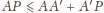 oraz
oraz
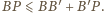 Dodając te trzy nierówności stronami,
otrzymujemy
Dodając te trzy nierówności stronami,
otrzymujemy
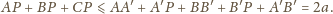
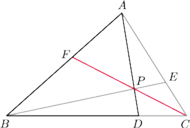
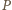 jest jednym z wierzchołków trójkąta
jest jednym z wierzchołków trójkąta
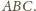
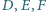 należą odpowiednio do boków
należą odpowiednio do boków
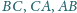 trójkąta
trójkąta
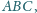 proste
proste
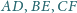 przecinają się w punkcie
przecinają się w punkcie
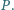 Wykaż, że
Wykaż, że

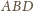 i prostej
i prostej
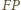 zachodzi
zachodzi
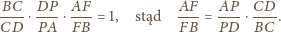
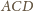 i prostej
i prostej
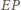 otrzymujemy
otrzymujemy

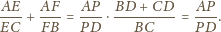
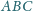 punkty
punkty
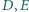 są spodkami dwusiecznych
odpowiednio
są spodkami dwusiecznych
odpowiednio
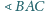 i
i
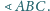 Punkt
Punkt
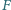 jest spodkiem
dwusiecznej kąta zewnętrznego przy wierzchołku
jest spodkiem
dwusiecznej kąta zewnętrznego przy wierzchołku
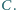 Udowodnij, że
punkty
Udowodnij, że
punkty
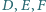 leżą na jednej prostej.
leżą na jednej prostej.
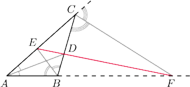
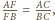
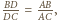
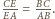 Zachodzi więc równość z Twierdzenie Menelaosa, co
kończy dowód.
Zachodzi więc równość z Twierdzenie Menelaosa, co
kończy dowód.
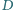 i
i
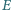 leżą odpowiednio na bokach
leżą odpowiednio na bokach
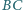 i
i
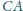 trójkąta
trójkąta
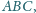 a punkt
a punkt
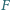 na przedłużeniu boku
na przedłużeniu boku
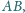 przy czym punkty
przy czym punkty
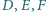 są współliniowe. Punkty
są współliniowe. Punkty
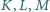 są odpowiednio środkami boków
są odpowiednio środkami boków
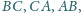 zaś punkty
zaś punkty
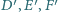 – obrazami symetrycznymi punktów
– obrazami symetrycznymi punktów
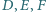 w symetriach względem
w symetriach względem
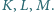 Wykaż, że punkty
Wykaż, że punkty
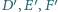 są
współliniowe.
są
współliniowe.
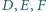
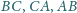
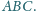
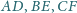

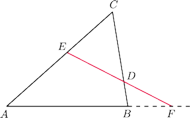
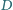
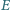
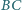
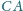
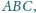
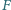
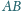
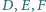
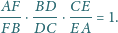
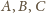 na prostą
na prostą
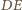 i zastosuj twierdzenie
Talesa.
i zastosuj twierdzenie
Talesa.
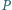 leży wewnątrz równoległoboku
leży wewnątrz równoległoboku
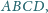 przy czym
środek odcinka
przy czym
środek odcinka
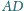 jest jednakowo odległy od punktów
jest jednakowo odległy od punktów
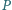 i
i
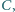 a środek odcinka
a środek odcinka
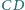 jest jednakowo odległy od punktów
jest jednakowo odległy od punktów
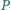 i
i
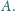 Punkt
Punkt
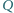 jest środkiem odcinka
jest środkiem odcinka
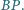 Wykazać, że
Wykazać, że
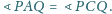
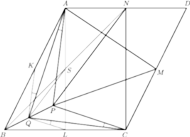
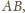
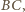
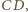
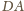 odpowiednio przez
odpowiednio przez
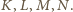 W myśl założenia,
W myśl założenia,
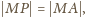
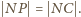 Niech
Niech
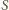 będzie wspólnym środkiem przekątnych
będzie wspólnym środkiem przekątnych
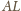 i
i
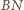 równoległoboku
równoległoboku
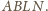 Odcinek
Odcinek
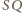 łączy środki
dwóch boków trójkąta
łączy środki
dwóch boków trójkąta
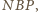 więc
więc
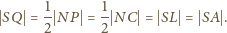
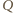 leży na okręgu o średnicy
leży na okręgu o średnicy
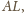 wobec czego kąt
wobec czego kąt
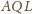 jest prosty. Analogicznie, kąt
jest prosty. Analogicznie, kąt
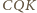 jest prosty. Stąd
wynika, że
jest prosty. Stąd
wynika, że
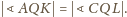 Punkty
Punkty
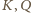 są środkami
dwóch boków trójkąta
są środkami
dwóch boków trójkąta
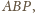 więc
więc
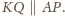 Analogicznie,
Analogicznie,
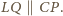 Stąd, ostatecznie,
Stąd, ostatecznie,
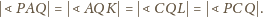
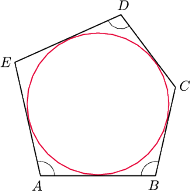
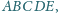 w którym
w którym
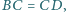
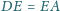 oraz
oraz
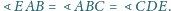 Wykazać, że
w pięciokąt
Wykazać, że
w pięciokąt
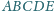 można wpisać okrąg.
można wpisać okrąg.
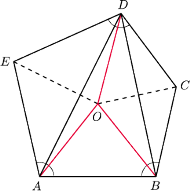
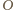 punkt przecięcia dwusiecznych kątów
punkt przecięcia dwusiecznych kątów
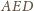 i
i
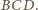
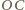 i
i
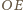 są symetralnymi odpowiednio odcinków
są symetralnymi odpowiednio odcinków
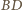 i
i
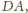 a więc punkt
a więc punkt
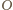 jest środkiem okręgu
opisanego na trójkącie
jest środkiem okręgu
opisanego na trójkącie
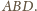 Zatem
Zatem
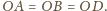 Wobec tego trójkąty
Wobec tego trójkąty
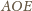 i
i
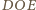 są przystające (cecha
bok-bok-bok), skąd
są przystające (cecha
bok-bok-bok), skąd
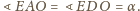 Analogicznie otrzymujemy
Analogicznie otrzymujemy
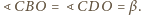 Ponadto
Ponadto
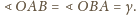 Stąd
korzystając z danych w treści zadania równości kątów, wnioskujemy, że
Stąd
korzystając z danych w treści zadania równości kątów, wnioskujemy, że
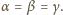 Zależności te z kolei dowodzą, że punkt
Zależności te z kolei dowodzą, że punkt
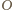 leży na
dwusiecznych kątów
leży na
dwusiecznych kątów
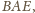
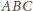 i
i
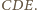
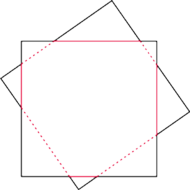
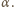 Oznaczając sumę długości
kolorowych odcinków ciągłych przez
Oznaczając sumę długości
kolorowych odcinków ciągłych przez
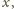 a przerywanych przez
a przerywanych przez
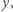 widać, że obwód jednego kwadratu jest równy
widać, że obwód jednego kwadratu jest równy
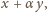 a drugiego
a drugiego
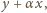 co po przyrównaniu daje
co po przyrównaniu daje
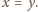
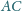 i
i
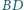 czworokąta wypukłego
czworokąta wypukłego
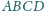 przecinają
się w punkcie
przecinają
się w punkcie
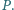 Punkt
Punkt
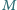 jest środkiem boku
jest środkiem boku
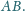 Prosta
Prosta
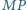 przecina bok
przecina bok
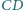 w punkcie
w punkcie
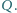 Udowodnij, że
stosunek pól trójkątów
Udowodnij, że
stosunek pól trójkątów
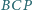 i
i
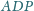 jest równy stosunkowi
długości odcinków
jest równy stosunkowi
długości odcinków
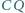 i
i
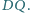
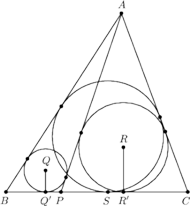
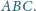 Rozważamy punkt
Rozważamy punkt
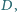 zmieniający swoje
położenie na boku
zmieniający swoje
położenie na boku
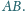 Prosta styczna do okręgów wpisanych
w trójkąty
Prosta styczna do okręgów wpisanych
w trójkąty
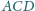 i
i
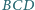 , rozłączna z odcinkiem
, rozłączna z odcinkiem
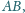 przecina odcinek
przecina odcinek
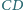 w punkcie
w punkcie
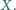 Udowodnić, że wszystkie
uzyskane w ten sposób punkty
Udowodnić, że wszystkie
uzyskane w ten sposób punkty
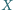 leżą na pewnym okręgu.
leżą na pewnym okręgu.
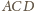 i
i
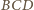 są
styczne do boku
są
styczne do boku
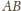 odpowiednio w punktach
odpowiednio w punktach
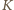 i
i
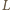 ;
do prostej przechodzącej przez
;
do prostej przechodzącej przez
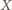 – odpowiednio w punktach
– odpowiednio w punktach
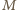 i
i
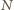 ; zaś do odcinka
; zaś do odcinka
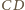 – odpowiednio w punktach
– odpowiednio w punktach
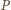 i
i
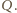
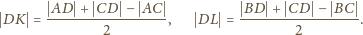
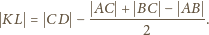
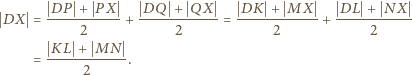
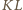 i
i
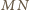 są symetryczne względem wspólnej osi
symetrii obu okręgów. Możemy zatem przepisać ostatnią równość jako
są symetryczne względem wspólnej osi
symetrii obu okręgów. Możemy zatem przepisać ostatnią równość jako
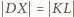 .
.
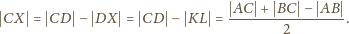
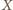 leży na okręgu o środku
leży na okręgu o środku
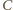 i promieniu
zależnym jedynie od trójkąta
i promieniu
zależnym jedynie od trójkąta
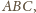 a nie od położenia punktu
a nie od położenia punktu
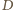 na boku
na boku