Dziewiąty miesiąc roku jest kolejnym, w którym dnia szybko ubywa. Na początku września Słońce góruje wciąż bliżej zenitu niż horyzontu, przebywając na nieboskłonie przez ponad 13,5 godziny, lecz do jego końca wysokość ta zmniejsza się o około 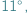do mniej więcej 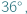a dzień skróci się poniżej 12 godzin. Słońce przetnie równik niebieski w drodze na południe, rozpoczynając na naszej półkuli Ziemi astronomiczną jesień 23 września o godzinie 9:50 naszego czasu. Jednak ze względu na refrakcję atmosferyczną faktyczna równonoc nastąpi u nas 2-3 dni później.

W sierpniu 2017 roku astronomowie "grawitacyjni" (skupieni w zespołach LIGO i Virgo) zaobserwowali pierwszą bezpośrednią detekcję fal grawitacyjnych emitowanych podczas połączenia się dwóch gwiazd neutronowych w układzie podwójnym. Wydarzenie to, oznaczone GW170817, było początkiem astronomii wieloaspektowej z udziałem detektorów fal grawitacyjnych, ponieważ falom grawitacyjnym towarzyszyły fale elektromagnetyczne, m.in. błysk gamma. Dokładna lokalizacja sygnału na niebie dostarczona przez LIGO i Virgo umożliwiła ponad 70 teleskopom obserwacje poświaty zdarzenia w świetle optycznym, promieniach rentgenowskich, radiowych i innych.

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

Kiedy wysokoenergetyczna cząstka przechodząca przez gęsty ośrodek dielektryczny zderzy się z którąś z cząstek budujących ten ośrodek, może powstawać wiele nowych cząstek, m.in. fotonów, elektronów i pozytonów, które tworzą swoistą kaskadę cząstek. Taka kaskada może mieć kilka centymetrów długości i jest stosunkowo szybka, gdyż tworzące ją cząstki niejednokrotnie poruszają się z prędkościami przewyższającymi prędkość światła w tym ośrodku...

Każdy czytelnik Delty wie, że jednym z podstawowych pojęć w matematyce jest funkcja. Matematycy nie tylko odmieniają to słowo przez wszystkie przypadki (może z wyjątkiem wołacza), ale również tworzą od niego słowa pochodne (mamy wszak równania funkcyjne czy analizę funkcjonalną). Część czytelników Delty wie również, że programiści nie pozostają matematykom dłużni - funkcje zrobiły w programowaniu doprawdy zawrotną karierę i są obecne w zdecydowanej większości języków programowania. Spróbujemy wyjaśnić, czym różni się "funkcja" matematyka od "funkcji" programisty.

Tytuł niniejszego artykułu jest zestawieniem dwóch pozornie odległych pojęć matematycznych. Pierwszym z nich jest trójkąt Sierpińskiego - jeden z najlepiej rozpoznawalnych fraktali. Drugim jest gra w życie - automat komórkowy opisany w 1970 roku przez Johna Conwaya.

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

W artykule rozważymy geometryczny problem, do którego sformułowania użyjemy motywacji astronomicznych. Załóżmy, że chcemy sprawdzić, czy najbliższa naszej intuicji szkolna geometria, zwana geometrią euklidesową, opisuje Wszechświat. Naturalną próbą odpowiedzi będzie eksperymentalne sprawdzenie, czy twierdzenia tej geometrii zachodzą w otaczającej nas przestrzeni. Na przykład możemy zbadać, czy suma kątów wewnętrznych trójkąta utworzonego przez punkt na Ziemi i dwa punkty na różnych odległych gwiazdach wynosi 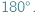Jednakże wszystkie takie sprawdzenia tego i innych twierdzeń geometrii euklidesowej możemy wykonać jedynie w pewnym otoczeniu Ziemi, którego promień jest wyznaczony zasięgiem naszych teleskopów...

Gdy w zadaniu występuje kąt o mierze będącej wielokrotnością 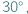to jest spora szansa na to, że gdzieś tam jest ukryty trójkąt równoboczny.

W salonie fryzjerskim siedzi matematyk, obok leży połyskująca para nożyczek, mnóstwo szczotek i innych sprzętów. Matematyk nerwowo wierci się w fotelu - przecież nie od dziś wie, że sfery zaczesać się nie da. Fryzjer intuicyjnie sięga po nożyczki, szalejące nad czołem rozmaitości nie rokują zbyt dobrze. Niechętny rozspójnieniu klient wpada na pomysł - warkocz będzie idealny!

Modelowanie matematyczne jest pewnego rodzaju sztuką opisywania świata - zarówno w skali mikro, jak i makro - za pomocą równań matematycznych (równań różniczkowych, różnicowych czy stochastycznych). Opis mikroskopowy może dotyczyć zachowania pojedynczych molekuł (cząsteczek), natomiast obiektem opisu makroskopowego jest to, co widzimy "gołym okiem", m.in. przemiany zachodzące w wyniku reakcji chemicznych. Mogą to być zmiany właściwości fizycznych danych substancji (np. stan skupienia, barwa, gęstość) lub chemicznych (np. zapach, smak, toksyczność)...

W pierwszej połowie XX wieku znaczący postęp prac nad matematycznymi modelami zjawisk losowych doprowadził do powstania wyodrębnionego działu matematyki wykorzystującego zaawansowane metody algebry i analizy matematycznej. Tematów badawczych dostarczały pytania stawiane przez specjalistów różnych dziedzin. Abstrahowanie od szczegółowych cech badanych zjawisk w procesie modelowania matematycznego niejednokrotnie prowadziło do zbliżonych opisów różnych zagadnień. Dzisiaj mówimy o zastosowaniach rachunku prawdopodobieństwa, które posiłkują się teorią procesów stochastycznych i statystyką. Jednolity model matematyczny stawał się także narzędziem do wykorzystania przy badaniu zagadnień, do analizy których nie wykorzystywano wcześniej metod matematycznych...

Istnieje taka gałąź biologii molekularnej, która obecnie przynosi ważne odkrycia prawie co miesiąc. I nie są to badania żyjących obecnie, bogatych w osobniki, gatunków zwierząt, roślin, mikroorganizmów. Szeroko o tym kierunku badań traktuje świeżo wydana książka Davida Reicha: "Kim jesteśmy, skąd przyszliśmy… Kopalny DNA i nowa nauka o przeszłości człowieka". Wersja oryginalna ukazała się w języku angielskim w 2018 roku; dzięki czujności wydawnictwa CiS i tłumaczowi, Piotrowi Szwajcerowi, polski czytelnik ma już ułatwiony dostęp do kopalni najbardziej aktualnej wiedzy w omawianym temacie.

Gdy dobiegła końca I wojna światowa, rozpoczęto realizację wielu zamierzeń, które w latach wojennych nie mogły zostać urzeczywistnione. Dotyczyło to także matematyki.

Warszawscy matematycy postanowili, że w 2018 roku będą świętować stulecie Warszawskiej Szkoły Matematycznej. W roku 2018 cały naród świętował odzyskanie niepodległości, ale dlaczego ten właśnie rok uznajemy za rok powstania WSM? Otóż w tym czasie ukazał się drukiem artykuł, autorstwa Zygmunta Janiszewskiego, "O potrzebach matematyki w Polsce", który został uznany za manifest całego pokolenia matematyków i jednocześnie zainicjował polską szkołę matematyki.

Gdyby Leo Wienera nie ciągnęło tak bardzo w świat, jego syn Norbert, wybitny matematyk i twórca cybernetyki, mógłby urodzić się w Białymstoku, tak jak Leo. Matka Norberta, Bertha Kahn, urodziła się co prawda w USA, ale jej ojciec - Henry Kahn - pochodził z Hesse w Niemczech 1231 km od Białegostoku). Zarówno Kahnowie, jak i Wienerowie byli europejskimi Żydami z interesującymi rodowodami. Leo Wiener wymieniał słynnego filozofa żydowskiego Majmonidesa (1135-1204) jako jednego ze swych przodków.