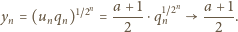Niech
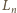 oznacza sumę po lewej stronie zależności, podanej
na początku zadania, zaś
oznacza sumę po lewej stronie zależności, podanej
na początku zadania, zaś
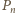 – ułamek po prawej stronie. Dla
– ułamek po prawej stronie. Dla
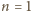 mamy
mamy
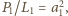 zatem równość
zatem równość
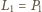 wymusza
wartość
wymusza
wartość
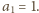 Dalej,
Dalej,
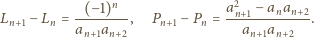
Widać więc, że podana zależność jest spełniona dla wszystkich
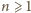 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
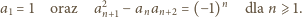 | (1) |
Jeżeli ciąg
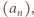 spełniający ten warunek, miałby również spełniać
rekurencję typu
spełniający ten warunek, miałby również spełniać
rekurencję typu
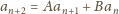 | (2) |
(z
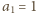 ), to dla
), to dla
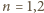 mielibyśmy
mielibyśmy

Pierwsza para równości to układ równań liniowych (z niewiadomymi
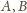 ) o wyznaczniku
) o wyznaczniku
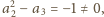 więc mający dokładnie
jedno rozwiązanie. Przy tym jest on spełniony dla
więc mający dokładnie
jedno rozwiązanie. Przy tym jest on spełniony dla
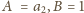 (co łatwo
stwierdzić, korzystając z drugiej pary równości). Stąd wniosek, że
jedynym kandydatem na postulowaną zależność rekurencyjną jest
równanie
(co łatwo
stwierdzić, korzystając z drugiej pary równości). Stąd wniosek, że
jedynym kandydatem na postulowaną zależność rekurencyjną jest
równanie
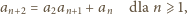 | (3) |
z warunkiem początkowym
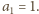 Wprowadźmy oznaczenia:
Wprowadźmy oznaczenia:
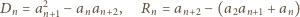
i zauważmy, że (dla
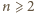 )
)
skąd przez odjęcie stronami
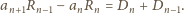 | (4) |
Ponadto (wobec
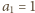 ) mamy:
) mamy:
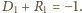
Wnioski: Jeżeli ciąg liczb całkowitych dodatnich
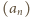 spełnia
wyjściową zależność, czyli warunki (1), to dla wszystkich
spełnia
wyjściową zależność, czyli warunki (1), to dla wszystkich
 mamy
mamy
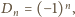 więc prawa strona (4) ma stale wartość 0; przy tym
więc prawa strona (4) ma stale wartość 0; przy tym
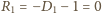 i ze wzoru (4) wynika, że
i ze wzoru (4) wynika, że
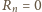 dla wszystkich
dla wszystkich
 – mamy zależność (3).
– mamy zależność (3).
Na odwrót, jeśli równanie (3) (z wyrazem początkowym
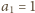 oraz
dowolnym
oraz
dowolnym
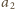 ) jest dla wszystkich
) jest dla wszystkich
 spełnione, czyli wszystkie
spełnione, czyli wszystkie
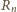 są zerami, to wobec (4):
są zerami, to wobec (4):
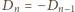 dla
dla
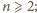 przy tym
przy tym
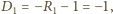 zatem
zatem
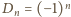 – a to jest zależność
(1).
– a to jest zależność
(1).
Ostatecznie więc, zadana na wstępie zależność jest równoważna rekurencji
liniowej (2) z parametrami
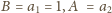 – dowolna liczba
naturalna.
– dowolna liczba
naturalna.
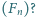

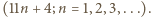 Ciąg Fibonacciego - a raczej jego początkowy odcinek - zapisany modulo
Ciąg Fibonacciego - a raczej jego początkowy odcinek - zapisany modulo 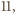 przedstawia się tak:
przedstawia się tak: 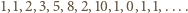 Dalej reszty (mod
Dalej reszty (mod 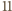 ) powtarzają się cyklicznie, z okresem
) powtarzają się cyklicznie, z okresem 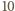 ; reszta
; reszta 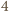 jest w tym ciągu nieobecna.
jest w tym ciągu nieobecna.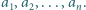 Ruch polega na wyborze dwóch takich indeksów
Ruch polega na wyborze dwóch takich indeksów 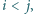 że
że 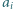 nie dzieli
nie dzieli 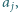 i zastąpieniu liczb
i zastąpieniu liczb 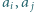 przez odpowiednio ich największy wspólny dzielnik i najmniejszą wspólną wielokrotność. Udowodnić, że nie jest możliwe wykonanie nieskończenie wielu ruchów.
przez odpowiednio ich największy wspólny dzielnik i najmniejszą wspólną wielokrotność. Udowodnić, że nie jest możliwe wykonanie nieskończenie wielu ruchów.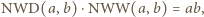 to iloczyn
to iloczyn 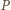 wszystkich wyrazów ciągu nie zmienia się po wykonaniu ruchu. W szczególności każdy z wyrazów ciągu jest ograniczony z góry przez
wszystkich wyrazów ciągu nie zmienia się po wykonaniu ruchu. W szczególności każdy z wyrazów ciągu jest ograniczony z góry przez 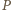 i ograniczony z dołu przez
i ograniczony z dołu przez 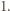 Ponadto w każdym ruchu, modyfikującym pewne wyrazy o indeksach
Ponadto w każdym ruchu, modyfikującym pewne wyrazy o indeksach 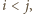 liczba
liczba 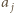 jest zamieniana na większą
jest zamieniana na większą 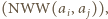 liczba
liczba 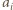 zaś - na mniejszą
zaś - na mniejszą 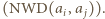 Żaden wyraz ciągu nie może być nieskończenie wiele razy zmniejszany (jako ograniczony z dołu przez
Żaden wyraz ciągu nie może być nieskończenie wiele razy zmniejszany (jako ograniczony z dołu przez 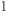 ) ani zwiększany (jako ograniczony z góry przez
) ani zwiększany (jako ograniczony z góry przez 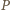 ). W takim razie każdy wyraz zostanie zmieniony skończenie wiele razy, czyli nie możemy wykonać nieskończenie wielu ruchów.
). W takim razie każdy wyraz zostanie zmieniony skończenie wiele razy, czyli nie możemy wykonać nieskończenie wielu ruchów.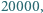 które tworzą ciąg arytmetyczny.
które tworzą ciąg arytmetyczny.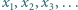 o wyrazach całkowitych dodatnich, w którym każda dodatnia liczba całkowita występuje jednokrotnie, przy czym dla każdego
o wyrazach całkowitych dodatnich, w którym każda dodatnia liczba całkowita występuje jednokrotnie, przy czym dla każdego  suma
suma 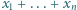 jest podzielna przez
jest podzielna przez 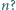
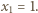 Będziemy przedłużać zdefiniowany odcinek ciągu, dołączając po dwa wyrazy.
Będziemy przedłużać zdefiniowany odcinek ciągu, dołączając po dwa wyrazy.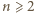 i przyjmijmy, że wyrazy
i przyjmijmy, że wyrazy 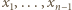 są już określone. Najmniejsza dodatnia liczba całkowita, różna od
są już określone. Najmniejsza dodatnia liczba całkowita, różna od 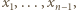 będzie wyrazem
będzie wyrazem 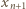 (to gwarantuje, że w budowanym ciągu znajdą się wszystkie liczby całkowite dodatnie).
(to gwarantuje, że w budowanym ciągu znajdą się wszystkie liczby całkowite dodatnie).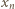 wzorem
wzorem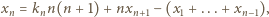
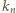 jest liczbą całkowitą tak dobraną, by uzyskana liczba
jest liczbą całkowitą tak dobraną, by uzyskana liczba 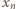 była dodatnia oraz różna od liczb
była dodatnia oraz różna od liczb 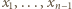 i różna od
i różna od 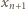 (powstający ciąg będzie więc miał wszystkie wyrazy różne). Przy tym
(powstający ciąg będzie więc miał wszystkie wyrazy różne). Przy tym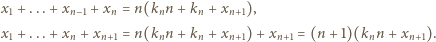
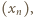 jakiego szukamy.
jakiego szukamy.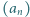 jest określony wzorem rekurencyjnym:
jest określony wzorem rekurencyjnym: 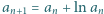 ; wyraz początkowy
; wyraz początkowy 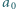 jest dowolną liczbą większą od 1. Udowodnić, że ciąg
jest dowolną liczbą większą od 1. Udowodnić, że ciąg 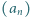 jest asymptotycznie równy ciągowi
jest asymptotycznie równy ciągowi 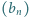 o wyrazach
o wyrazach 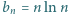 ; to znaczy,
; to znaczy,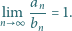
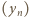 jest ciągiem rosnącym do nieskończoności, wówczas równość
jest ciągiem rosnącym do nieskończoności, wówczas równość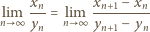
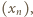 dla którego granica po prawej stronie istnieje. Ponieważ
dla którego granica po prawej stronie istnieje. Ponieważ 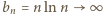 rosnąco, twierdzenie ma szanse zadziałać - warto zająć się ciągiem o wyrazach
rosnąco, twierdzenie ma szanse zadziałać - warto zająć się ciągiem o wyrazach 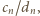 gdzie
gdzie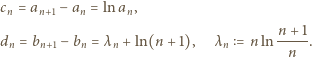
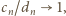 wzór (1) (dla
wzór (1) (dla 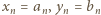 ) da wynik
) da wynik 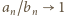 i zakończy rozwiązanie.
i zakończy rozwiązanie.
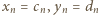 ); ciąg
); ciąg 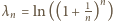 jest rosnący, więc
jest rosnący, więc 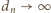 rosnąco. Chcemy dowieść, że liczba 1 jest granicą ciągu o wyrazach
rosnąco. Chcemy dowieść, że liczba 1 jest granicą ciągu o wyrazach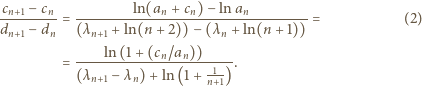
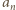 są większe od 1 (oczywista indukcja); ich logarytmy są dodatnie, wobec czego ciąg
są większe od 1 (oczywista indukcja); ich logarytmy są dodatnie, wobec czego ciąg 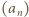 jest rosnący - ma zatem granicę (skończoną lub nie). Granica skończona musiałaby być liczbą
jest rosnący - ma zatem granicę (skończoną lub nie). Granica skończona musiałaby być liczbą 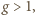 spełniającą równanie
spełniającą równanie 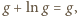 co nie jest możliwe. Tak więc
co nie jest możliwe. Tak więc 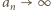 ; co za tym idzie,
; co za tym idzie, 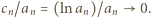 Korzystając ze znanej relacji granicznej
Korzystając ze znanej relacji granicznej 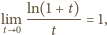 możemy teraz napisać
możemy teraz napisać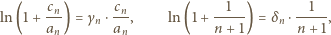
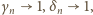 i przepisać wyrażenie (2) w postaci
i przepisać wyrażenie (2) w postaci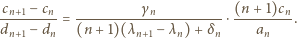
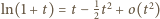 (przy
(przy 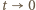 ) możemy wywnioskować, że
) możemy wywnioskować, że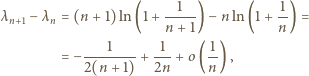
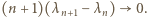 Zatem cały pierwszy czynnik iloczynu po prawej stronie wzoru (3) dąży do 1. Pozostaje dowieść, że drugi czynnik też - czyli że
Zatem cały pierwszy czynnik iloczynu po prawej stronie wzoru (3) dąży do 1. Pozostaje dowieść, że drugi czynnik też - czyli że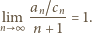
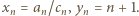 Granica po lewej stronie (4) będzie równa granicy
Granica po lewej stronie (4) będzie równa granicy 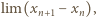 jeśli ta ostatnia istnieje. Skoro
jeśli ta ostatnia istnieje. Skoro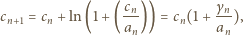
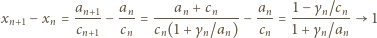
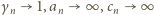 ). To dowodzi słuszności tezy (4), więc i tezy zadania.
). To dowodzi słuszności tezy (4), więc i tezy zadania.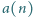 oznacza odległość liczby naturalnej
oznacza odległość liczby naturalnej 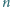 od najbliższej liczby, będącej pełnym kwadratem:
od najbliższej liczby, będącej pełnym kwadratem: 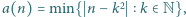 i niech
i niech 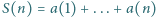 oraz
oraz 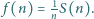 Udowodnić, że każda dodatnia liczba całkowita występuje w ciągu
Udowodnić, że każda dodatnia liczba całkowita występuje w ciągu 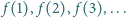 dokładnie trzykrotnie.
dokładnie trzykrotnie.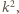 mają postać
mają postać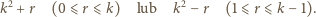
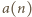 dla tych liczb wynosi
dla tych liczb wynosi 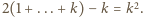 Stąd
Stąd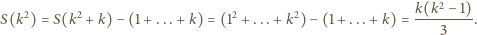
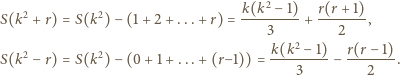
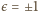 i wyznaczamy
i wyznaczamy 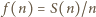 (dla
(dla 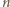 w formie (1)):
w formie (1)):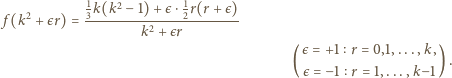

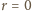 oraz
oraz 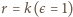 wychodzą wartości niecałkowite - można je zignorować, ograniczając zakres parametru
wychodzą wartości niecałkowite - można je zignorować, ograniczając zakres parametru  do
do 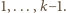 Wówczas
Wówczas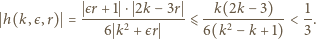
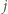 ) wtedy i tylko wtedy, gdy
) wtedy i tylko wtedy, gdy 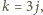 zaś
zaś 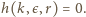 Gdy
Gdy 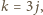 ostatni warunek
ostatni warunek 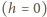 jest spełniony dla trzech par
jest spełniony dla trzech par 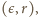 mianowicie
mianowicie 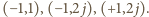
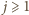 jest wartością wyrażenia
jest wartością wyrażenia 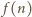 jedynie dla
jedynie dla 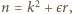 gdzie
gdzie 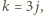 zaś
zaś  jest jedną z trzech powyższych par - czyli, po podstawieniu, dla
jest jedną z trzech powyższych par - czyli, po podstawieniu, dla 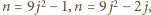
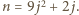
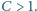 Ciąg dodatnich liczb rzeczywistych
Ciąg dodatnich liczb rzeczywistych 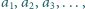 w którym
w którym 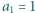 i
i 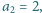 spełnia warunki
spełnia warunki 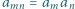 oraz
oraz 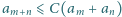 dla
dla 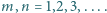 Dowieść, że
Dowieść, że 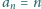 dla
dla 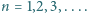
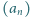 spełnia warunki:
spełnia warunki: 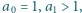
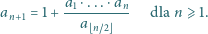
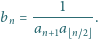
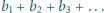 jest zbieżny, a jego suma jest liczbą wymierną.
jest zbieżny, a jego suma jest liczbą wymierną.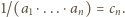 Liczby
Liczby 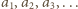 są całkowite i większe od 1, czyli większe lub równe 2. Zatem
są całkowite i większe od 1, czyli większe lub równe 2. Zatem 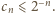
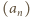 wynika, że
wynika, że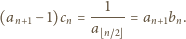
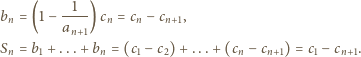
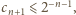 widzimy, że
widzimy, że 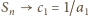 przy
przy 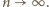 Jest to suma szeregu
Jest to suma szeregu 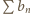 ; i oczywiście jest to liczba wymierna.
; i oczywiście jest to liczba wymierna.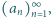 że
że
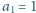 oraz, dla każdego
oraz, dla każdego
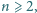
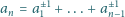
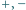 w wykładnikach. Znaleźć
najmniejszą możliwą wartość
w wykładnikach. Znaleźć
najmniejszą możliwą wartość
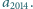
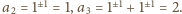 Oczywiście, dla każdego
Oczywiście, dla każdego
 zachodzi
zachodzi
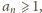 a więc również
a więc również
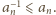 W takim razie dla
W takim razie dla
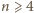 mamy
mamy
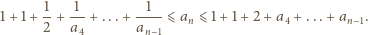
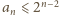 dla
dla
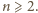 Wówczas jednak pierwsza
nierówność daje oszacowanie
Wówczas jednak pierwsza
nierówność daje oszacowanie
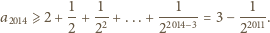
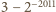 jest osiągana przez
jest osiągana przez
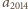 dla ciągu
określonego przez warunek
dla ciągu
określonego przez warunek
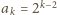 dla
dla
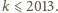 Faktycznie
wówczas
Faktycznie
wówczas
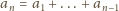
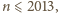 oraz
oraz
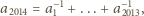
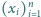 liczb rzeczywistych
dodatnich prawdziwa jest nierówność
liczb rzeczywistych
dodatnich prawdziwa jest nierówność
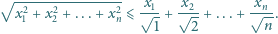
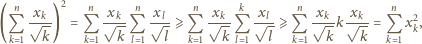
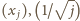 są malejące.
są malejące.
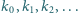 taki, że dla każdego
taki, że dla każdego
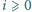 iloczyn
iloczyn
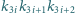 jest
podzielny przez każdą z liczb
jest
podzielny przez każdą z liczb
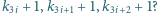
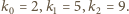 Przyjmijmy, że wyrazy
Przyjmijmy, że wyrazy
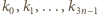 są
już określone i tworzą ciąg rosnący długości
są
już określone i tworzą ciąg rosnący długości
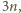 spełniający
wymagany warunek. Oznaczmy dla wygody:
spełniający
wymagany warunek. Oznaczmy dla wygody:
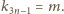 Określamy
kolejne trzy wyrazy:
Określamy
kolejne trzy wyrazy:
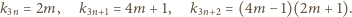
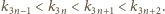 Pozostaje sprawdzić, że iloczyn
trzech wypisanych liczb, równy
Pozostaje sprawdzić, że iloczyn
trzech wypisanych liczb, równy
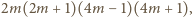 dzieli się
przez każdą z tych liczb, powiększoną o 1, czyli przez liczby
dzieli się
przez każdą z tych liczb, powiększoną o 1, czyli przez liczby
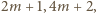
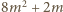 ; a to jest oczywiste. Kontynuując, otrzymujemy nieskończony
ciąg
; a to jest oczywiste. Kontynuując, otrzymujemy nieskończony
ciąg
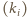 o żądanych własnościach.
o żądanych własnościach.
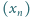 jest określony wzorem rekurencyjnym
jest określony wzorem rekurencyjnym
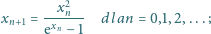
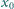 jest dowolną liczbą dodatnią. Obliczyć
granicę
jest dowolną liczbą dodatnią. Obliczyć
granicę
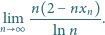
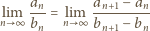
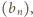 rosnącego do nieskończoności, i dla każdego
ciągu
rosnącego do nieskończoności, i dla każdego
ciągu
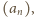 dla którego granica po prawej stronie istnieje.
dla którego granica po prawej stronie istnieje.
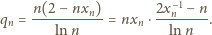
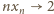 ; pozostaje zająć się
drugim czynnikiem. We wzorze Stolza przyjmijmy
; pozostaje zająć się
drugim czynnikiem. We wzorze Stolza przyjmijmy
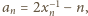
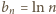 :
:
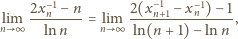
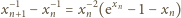
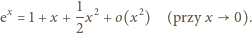
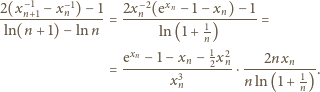
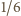 (nieco
dłuższy fragment rozwinięcia
(nieco
dłuższy fragment rozwinięcia
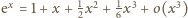 ).
Drugi czynnik: licznik dąży do 4, mianownik do 1. Cały iloczyn dąży do
).
Drugi czynnik: licznik dąży do 4, mianownik do 1. Cały iloczyn dąży do
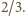 Tyle więc wynosi granica napisana po lewej stronie równości (2).
Wracamy do równości (1), pamiętając, że
Tyle więc wynosi granica napisana po lewej stronie równości (2).
Wracamy do równości (1), pamiętając, że
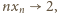 i otrzymujemy
ostatecznie
i otrzymujemy
ostatecznie
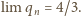
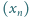 jest określony wzorem rekurencyjnym
jest określony wzorem rekurencyjnym

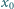 jest dowolną liczbą dodatnią. Obliczyć granicę
jest dowolną liczbą dodatnią. Obliczyć granicę
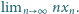
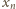 są liczbami dodatnimi. Z nierówności
są liczbami dodatnimi. Z nierówności
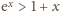 (dla
(dla
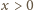 ) wynika, że ciąg
) wynika, że ciąg
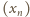 jest malejący –
zatem zbieżny do granicy
jest malejący –
zatem zbieżny do granicy
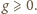 Równanie
Równanie
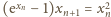 daje
w granicy zależność
daje
w granicy zależność
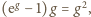 która nie zachodzi dla
żadnej liczby dodatniej
która nie zachodzi dla
żadnej liczby dodatniej
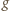 (w myśl tej samej nierówności). Zatem
(w myśl tej samej nierówności). Zatem
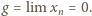
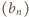 jest ciągiem
rosnącym do nieskończoności, to
jest ciągiem
rosnącym do nieskończoności, to
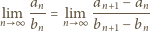
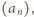 dla którego granica po prawej stronie
istnieje.
dla którego granica po prawej stronie
istnieje.
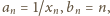 mamy w mianowniku wyrażenia po prawej
stronie jedynkę, a w liczniku:
mamy w mianowniku wyrażenia po prawej
stronie jedynkę, a w liczniku:
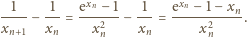
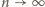 (więc
(więc
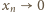 ), ten iloraz dąży do
), ten iloraz dąży do
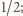 widać
to na przykład z początkowego fragmentu rozwinięcia potęgowego
widać
to na przykład z początkowego fragmentu rozwinięcia potęgowego
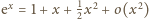 (przy
(przy
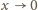 ). Tak więc
). Tak więc
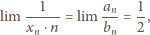
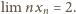
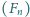 będzie ciągiem Fibonacciego:
będzie ciągiem Fibonacciego:

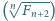 jest malejący.
jest malejący.
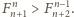 Dla
Dla
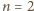 to prawda
to prawda
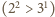 . Dalej przyjmujemy
. Dalej przyjmujemy
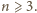 Korzystamy ze wzoru
Korzystamy ze wzoru
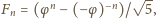 gdzie
gdzie
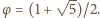 Oznaczmy:
Oznaczmy:
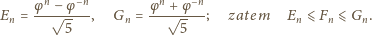
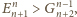 czyli
czyli
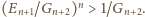 A ponieważ
A ponieważ
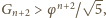 wystarczy dowieść, że
wystarczy dowieść, że
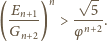
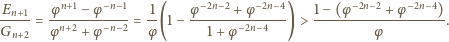
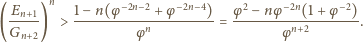
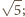 jest to równoważne nierówności
jest to równoważne nierówności
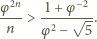
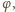 sprawdzamy, że nierówność (2)
zachodzi dla
sprawdzamy, że nierówność (2)
zachodzi dla
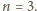 Zachodzi więc dla wszystkich
Zachodzi więc dla wszystkich
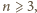 bo
wyrażenie po lewej stronie (2) przedstawia ciąg rosnący. To kończy
dowód.
bo
wyrażenie po lewej stronie (2) przedstawia ciąg rosnący. To kończy
dowód.
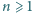 zachodzą następujące
równości:
zachodzą następujące
równości:
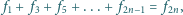
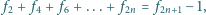
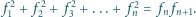
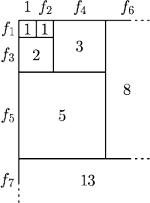
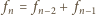 – następny kwadrat „pasuje” do
dwóch poprzednich.
– następny kwadrat „pasuje” do
dwóch poprzednich.
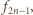 to cały prostokąt
ma taką właśnie szerokość, a wysokość równą następnemu
wyrazowi ciągu, czyli
to cały prostokąt
ma taką właśnie szerokość, a wysokość równą następnemu
wyrazowi ciągu, czyli
 Jednocześnie wysokość ta jest
równa
Jednocześnie wysokość ta jest
równa

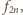 to prostokąt ma szerokość
równą
to prostokąt ma szerokość
równą
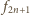 i zarazem równą
i zarazem równą
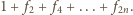
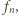 to
prostokąt
ma taką właśnie szerokość lub wysokość, a drugi z wymiarów
równy
to
prostokąt
ma taką właśnie szerokość lub wysokość, a drugi z wymiarów
równy
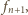 więc ma pole
więc ma pole
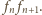 Jednocześnie pole to
jest równe
Jednocześnie pole to
jest równe
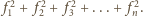

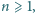
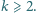
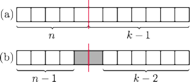
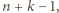 takich jak opisano
w poprzednim zadaniu, można rozciąć na chodnik o długości
takich jak opisano
w poprzednim zadaniu, można rozciąć na chodnik o długości
 (od
lewej strony) oraz chodnik o długości
(od
lewej strony) oraz chodnik o długości
 (po prawej stronie) bez
rozcinania poszczególnych płyt (
(po prawej stronie) bez
rozcinania poszczególnych płyt (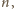 a po prawej chodnik długości
a po prawej chodnik długości
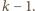 Z poprzedniego
zadania wiemy, że możliwości tych jest po lewej
Z poprzedniego
zadania wiemy, że możliwości tych jest po lewej
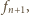 po prawej
po prawej
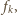 więc łącznie
więc łącznie
 Cięcie chodnika wymaga rozcinania płyty,
gdy w miejscu podziału leży płyta
Cięcie chodnika wymaga rozcinania płyty,
gdy w miejscu podziału leży płyta
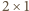 (
(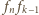 : układamy od lewej kolejno chodnik
długości
: układamy od lewej kolejno chodnik
długości
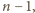 następnie płytę
następnie płytę
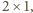 a po prawej chodnik
długości
a po prawej chodnik
długości
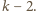 Wszystkich chodników, jak wiemy z poprzedniego
zadania, jest
Wszystkich chodników, jak wiemy z poprzedniego
zadania, jest
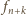 i każdy z nich da się rozciąć w opisany sposób
lub nie, stąd
i każdy z nich da się rozciąć w opisany sposób
lub nie, stąd
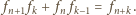
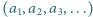 spełnia warunek
spełnia warunek
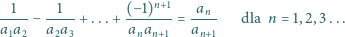
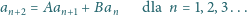
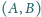 oraz wszystkie
pary wyrazów początkowych
oraz wszystkie
pary wyrazów początkowych
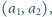 dla których ta rekurencja liniowa
generuje ciąg
dla których ta rekurencja liniowa
generuje ciąg
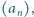 spełniający zadany na wstępie warunek.
spełniający zadany na wstępie warunek.
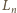 oznacza sumę po lewej stronie zależności, podanej
na początku zadania, zaś
oznacza sumę po lewej stronie zależności, podanej
na początku zadania, zaś
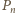 – ułamek po prawej stronie. Dla
– ułamek po prawej stronie. Dla
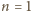 mamy
mamy
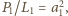 zatem równość
zatem równość
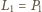 wymusza
wartość
wymusza
wartość
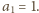 Dalej,
Dalej,
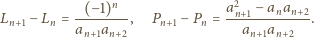
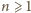 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
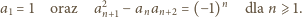
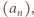 spełniający ten warunek, miałby również spełniać
rekurencję typu
spełniający ten warunek, miałby również spełniać
rekurencję typu
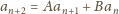
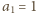 ), to dla
), to dla
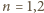 mielibyśmy
mielibyśmy

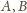 ) o wyznaczniku
) o wyznaczniku
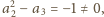 więc mający dokładnie
jedno rozwiązanie. Przy tym jest on spełniony dla
więc mający dokładnie
jedno rozwiązanie. Przy tym jest on spełniony dla
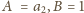 (co łatwo
stwierdzić, korzystając z drugiej pary równości). Stąd wniosek, że
jedynym kandydatem na postulowaną zależność rekurencyjną jest
równanie
(co łatwo
stwierdzić, korzystając z drugiej pary równości). Stąd wniosek, że
jedynym kandydatem na postulowaną zależność rekurencyjną jest
równanie
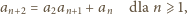
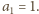 Wprowadźmy oznaczenia:
Wprowadźmy oznaczenia:
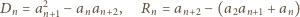
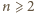 )
)
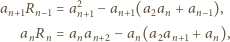
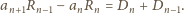
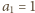 ) mamy:
) mamy:
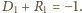
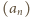 spełnia
wyjściową zależność, czyli warunki (1), to dla wszystkich
spełnia
wyjściową zależność, czyli warunki (1), to dla wszystkich
 mamy
mamy
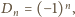 więc prawa strona (4) ma stale wartość 0; przy tym
więc prawa strona (4) ma stale wartość 0; przy tym
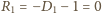 i ze wzoru (4) wynika, że
i ze wzoru (4) wynika, że
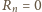 dla wszystkich
dla wszystkich
 – mamy zależność (3).
– mamy zależność (3).
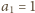 oraz
dowolnym
oraz
dowolnym
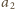 ) jest dla wszystkich
) jest dla wszystkich
 spełnione, czyli wszystkie
spełnione, czyli wszystkie
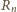 są zerami, to wobec (4):
są zerami, to wobec (4):
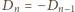 dla
dla
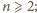 przy tym
przy tym
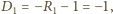 zatem
zatem
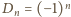 – a to jest zależność
(1).
– a to jest zależność
(1).
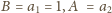 – dowolna liczba
naturalna.
– dowolna liczba
naturalna.
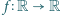 ma cykl długości
ma cykl długości
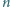 o początku
o początku
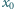 , gdy istnieje takie
, gdy istnieje takie
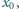 że liczby
że liczby
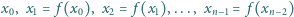 są parami różne, zaś
są parami różne, zaś
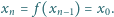
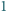 lub
lub
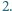
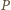 o współczynnikach
całkowitych ma cykl
o współczynnikach
całkowitych ma cykl
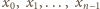 długości
długości
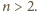 Mamy
Mamy
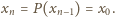 Kluczowa będzie dla nas obserwacja, że dla
dowolnych liczb całkowitych
Kluczowa będzie dla nas obserwacja, że dla
dowolnych liczb całkowitych
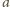 i
i
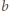 zachodzi
zachodzi
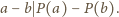
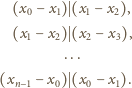
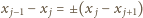
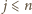 (przyjmujemy, że
(przyjmujemy, że
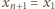 ). Znak „–” jest
wykluczony, gdyż liczby
). Znak „–” jest
wykluczony, gdyż liczby
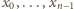 są parami różne. Mamy więc
są parami różne. Mamy więc
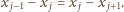 Oznacza to, że ciąg
Oznacza to, że ciąg
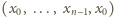 jest
arytmetyczny. Musi on być stały, co daje sprzeczność.
jest
arytmetyczny. Musi on być stały, co daje sprzeczność.
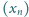 jest określony rekurencyjnie:
jest określony rekurencyjnie:
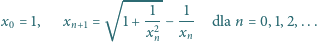
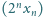 jest zbieżny i obliczyć jego granicę.
jest zbieżny i obliczyć jego granicę.
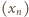 są liczbami dodatnimi. Zapiszmy każdy z nich jako
tangens pewnego kąta ostrego:
są liczbami dodatnimi. Zapiszmy każdy z nich jako
tangens pewnego kąta ostrego:
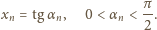
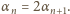 Zaczynamy od oczywistej zależności
Zaczynamy od oczywistej zależności
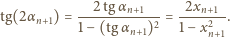
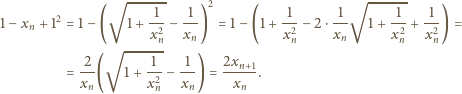
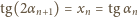
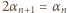 (obie liczby:
(obie liczby:
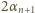 i
i
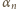 leżą
w przedziale
leżą
w przedziale
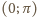 ). Tak więc
). Tak więc
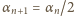 dla wszystkich
dla wszystkich
 ; a skoro
; a skoro
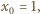 czyli
czyli
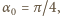 wnosimy stąd,
że
wnosimy stąd,
że

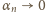 i skorzystać ze znanej relacji
granicznej
i skorzystać ze znanej relacji
granicznej
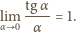
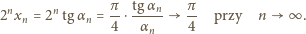
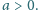 Określamy ciągi
Określamy ciągi
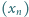 oraz
oraz
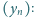
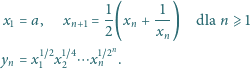
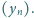
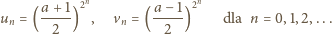
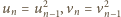 ;
;
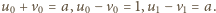
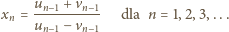
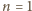 zgadza się. Przyjmijmy jej słuszność dla
zgadza się. Przyjmijmy jej słuszność dla
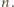 Wtedy dla
Wtedy dla
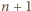 mamy
mamy
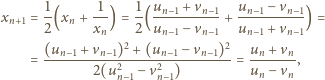
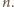 Teraz druga z zapowiedzianych
równości:
Teraz druga z zapowiedzianych
równości:
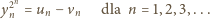
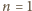 zgadza się. Weźmy
zgadza się. Weźmy
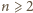 i załóżmy, że
równość analogiczna do (2) zachodzi dla
i załóżmy, że
równość analogiczna do (2) zachodzi dla
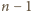 :
:
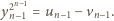
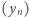 wynika, że
wynika, że
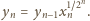 Stąd oraz
z (1):
Stąd oraz
z (1):
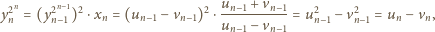
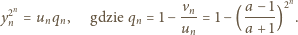
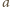 jest dodatnia, więc iloraz w nawiasie jest liczbą o module
mniejszym od 1. Wobec tego
jest dodatnia, więc iloraz w nawiasie jest liczbą o module
mniejszym od 1. Wobec tego
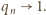 Stąd, ostatecznie,
Stąd, ostatecznie,