Każdej liczbie rzeczywistej możemy przypisać nieskończony ciąg cyfr jej rozwinięcia dziesiętnego. Jak wiadomo, jeżeli ciąg od pewnego miejsca się zapętla, to mamy do czynienia z liczbą wymierną. Inaczej rzecz ujmując, liczby wymierne mają okresowe rozwinięcie dziesiętne. Przyjmujemy tutaj, że tzw. rozwinięcie skończone jest rozwinięciem okresowym - od pewnego miejsca na każdej pozycji występuje wyłącznie cyfra 0.
Leonardo Fibonacci (1170-1240)
Fibonacci (właściwie Leonardo z Pizy, ok. 1170-1240) nauczył się zasad arytmetyki hindusko-arabskiej, gdy razem z ojcem przebywał w Bougie (obecnie algierska Bidżaja). Poszerzał swoją wiedzę podczas podróży do Egiptu, Syrii, Grecji, na Sycylię, do Prowansji. Gdy osiadł w Pizie, w 1202 roku napisał traktat Liber Abaci (Księga rachunków), z myślą o rozpowszechnieniu w Europie notacji dziesiętnej opartej na wykorzystaniu cyfr 0,1,2, ...,9. Pokazał w nim użyteczność nowych metod na wielu przykładach rachunkowych, szczególnie związanych z przeliczaniem miar i wag, obliczaniem zysków i odsetek, wymianą pieniędzy...
Tak zwana zasada indukcji przyrodniczej mówi: Gdy masz podejrzenie, że znalazłeś ogólny wzór, który działa dla każdej liczby naturalnej, to sprawdź go dla pierwszych paru wartości i dla jakiejś większej: jak wzór się zgadza, to zgadza się dla każdej liczby naturalnej...
Zbieżność to jedno z najważniejszych pojęć analizy matematycznej, odnoszące się najczęściej do ciągów i funkcji (oraz rozmaitych obiektów matematycznych skonstruowanych przy ich użyciu, np. szeregów czy ciągów funkcyjnych). Tu zajmiemy się zbieżnością ciągów liczbowych.
Jednym z naturalnych skojarzeń z nieskończonością są duże, bardzo duże liczby. Tak bardzo, że trudno je sobie wyobrazić, a intuicja nie pomaga. Możemy jednak o nich pomyśleć. Czytając doniesienia o wydatkach z budżetu państwa lub tym bardziej o światowej gospodarce, łatwo pogubić się w milionach, miliardach i bilionach. I chociaż wiemy, że w bilionie 
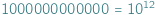mieści się aż milion milionów, mało kto jest w stanie to sobie wyobrazić. Wszystkie te liczby wpadają w tę samą kategorię - liczb dużych na tyle, że nie znajdujemy dla nich zastosowania w zwyczajnym codziennym życiu.
Teoria liczb Kącik początkującego olimpijczyka
Nieoczywiste zastosowania oczywistego stwierdzenia: pomiędzy dwiema kolejnymi liczbami całkowitymi nie ma żadnej liczby całkowitej.
Słynne twierdzenie Dirichleta głosi, że jeżeli liczby naturalne 
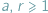są względnie pierwsze, to ciąg arytmetyczny 
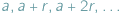zawiera nieskończenie wiele liczb pierwszych. Przedstawimy kilka wniosków płynących z tego twierdzenia.
W tym artykule chcemy zaprezentować pewną technikę dowodową zwaną interpretacją kombinatoryczną. Metoda ta pokazana będzie w działaniu: podajemy dwa zadania wraz z rozwiązaniami, które są ilustracją tematu.
Zbiór wszystkich liczb rzeczywistych 
nie jest równoliczny ze zbiorem wszystkich liczb naturalnych 
Tradycyjnie fraktale kojarzą nam się (często) z ładnymi rysunkami figur, które wykazują pewien zestaw cech odróżniających je od zwykłych obiektów. Nie precyzujemy tutaj uniwersalnego zestawu, gdyż sama definicja fraktala nie jest uniwersalna. W większości sytuacji chcemy, aby fraktal miał złożoną strukturę, spełniał pewne cechy samopodobieństwa oraz by nie dało się go zbyt prosto opisać geometrycznie. Mimo to często można go opisać względnie prosto pewnymi regułami rekurencyjnymi wykonywanymi na obiekcie startowym (lub zestawie takich obiektów).
Rys. 1 (a), (b), (c). Linie oznaczone strzałkami można rysować tylko zgodnie z ich kierunkiem
Które z rysunków 1 (a), (b), (c) da się narysować bez odrywania ołówka od kartki i bez rysowania ponownie wzdłuż narysowanej już linii?
Dawno, dawno temu, za drugą górą, za trzecią rzeką żył sobie królewicz Leonardo pochodzący ze szlachetnego rodu Fibonaccich. No, może nie całkiem królewicz, ale piąty syn dyplomaty włoskiego. Może nie całkiem za trzecią rzeką, bo urodził się za ósmą doliną i trzynastoma bagnami, dokładniej w Pizie w 1175 roku. Zatem przynajmniej rzeczywiście żył dawno, dawno temu. Choć w pewnym sensie żyje do dzisiaj w swoich uczniach, bowiem wieść o liczbach Fibonacciego rozeszła się po świecie i szumi o nich niejeden las...
Teoria liczb Konkurs prac uczniowskich
Skrót pracy nagrodzonej złotym medalem w konkursie Polskiego Towarzystwa Matematycznego i redakcji Delty na najlepszą pracę maturalną w roku 1978.
W 1964 roku amerykańsko-brytyjski matematyk Neil Sloane zaczął kolekcjonować znane ciągi liczb całkowitych. Niewinne hobby, motywowane zbadaniem własności kilku ciągów, które pojawiły się podczas pracy nad jego rozprawą doktorską, szybko przerodziło się w duże przedsięwzięcie. W efekcie zostały opublikowane dwie książki A Handbook of Integer Sequences (wydana w roku 1973, zawierająca 2372 ciągi) oraz The Encyclopedia of Integer Sequences (z 1995 roku, 5847 ciągi). W 1996 roku, gdy liczba zgromadzonych ciągów przekroczyła 10 000, dalsze ich przechowywanie w postaci książkowej stało się bardzo niepraktyczne...
W matematycznym świecie od zawsze znajdowało się mnóstwo tajemnic czekających na odkrycie. Tak zawiłych i zdradzieckich, że tylko szaleńcy mogli w ogóle wyobrazić sobie ich istnienie. Tymi szaleńcami byli nieustraszeni matematycy, którzy już od stuleci (jeżeli nie tysiącleci) szukają, rozwiązują i wyjaśniają zagadki, które większość ludzi już dawno uznawała za beznadziejne przypadki (lub są one tak abstrakcyjne, że w żaden sposób nieosiągalne).
Zdarza się czasem, że zachód słońca i pusta, piaszczysta plaża zachwycają nas, kiedy patrzymy na nie, spacerując brzegiem morza, jednak zamknięte w martwe ramy zdjęcia przywodzą na myśl co najwyżej słowo „kicz”. Ta historia, gdyby jeden z hollyłódzkich reżyserów zdecydował się nakręcić film na jej podstawie, wydałaby się z pewnością banalna. Tymczasem napisało ją życie.