Ciąg 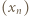 powstaje przez iterowanie funkcji
powstaje przez iterowanie funkcji 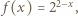 którą będziemy badać na przedziale
którą będziemy badać na przedziale ![[1,2].](/math/temat/matematyka/analiza/zadania/2018/03/25/zm-k44-759/3x-a051a26225a4472d5acd2ead6f6a678d0abff009-im-66,57,43-FF,FF,FF.gif) Ponieważ
Ponieważ 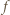 maleje od wartości
maleje od wartości 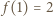 do wartości
do wartości 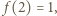 zatem odwzorowuje przedział
zatem odwzorowuje przedział ![[1,2]](/math/temat/matematyka/analiza/zadania/2018/03/25/zm-k44-759/7x-a051a26225a4472d5acd2ead6f6a678d0abff009-im-66,57,43-FF,FF,FF.gif) na siebie i ma w tym przedziale dokładnie jeden punkt stały
na siebie i ma w tym przedziale dokładnie jeden punkt stały 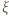 (tj. taki, że
(tj. taki, że 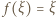 ). Obrazem przedziału
). Obrazem przedziału 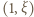 jest przedział
jest przedział 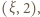 i na odwrót. Stąd wniosek, że wyrazy ciągu
i na odwrót. Stąd wniosek, że wyrazy ciągu 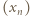 o numerach parzystych należą do jednego z tych przedziałów, a te o nieparzystych - do drugiego.
o numerach parzystych należą do jednego z tych przedziałów, a te o nieparzystych - do drugiego.
Równość 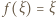 przepisujemy jako
przepisujemy jako 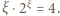 Funkcja
Funkcja 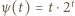 jest rosnąca; przy tym
jest rosnąca; przy tym
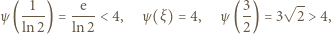
wobec czego
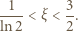 |
(1) |
Ponieważ (z założenia) 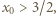 zatem
zatem 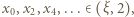 zaś
zaś 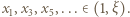
Użyjemy rachunku pochodnych. Oznaczmy (dla krótkości): 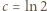 i zauważmy, że
i zauważmy, że 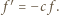 Niech
Niech 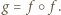 Wówczas
Wówczas
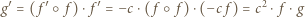
i dalej:
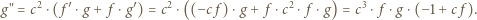 |
(2) |
Dla ![x ∈ [1,ξ]](/math/temat/matematyka/analiza/zadania/2018/03/25/zm-k44-759/1x-ebb224189cbd9ab5aa439f6248ce3382f71c3782-im-66,57,43-FF,FF,FF.gif) mamy nierówność
mamy nierówność 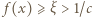 (por. (1)), więc wyrażenie w nawiasie po prawej stronie (2) ma w tych punktach wartość dodatnią. To znaczy, że funkcja
(por. (1)), więc wyrażenie w nawiasie po prawej stronie (2) ma w tych punktach wartość dodatnią. To znaczy, że funkcja 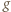 jest ściśle wypukła w przedziale
jest ściśle wypukła w przedziale ![|[1,ξ]](/math/temat/matematyka/analiza/zadania/2018/03/25/zm-k44-759/4x-ebb224189cbd9ab5aa439f6248ce3382f71c3782-im-66,57,43-FF,FF,FF.gif) ; a ponieważ
; a ponieważ 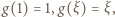 zatem
zatem
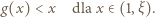 |
(3) |
Ciąg 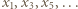 leży w przedziale
leży w przedziale 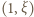 i jest generowany rekurencyjnie wzorem
i jest generowany rekurencyjnie wzorem 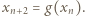 Nierówność (3) pokazuje, że jest to ciąg malejący, i w konsekwencji zbieżny. Jego granica musi być punktem stałym funkcji
Nierówność (3) pokazuje, że jest to ciąg malejący, i w konsekwencji zbieżny. Jego granica musi być punktem stałym funkcji 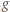 ; jednak nie ma takiego punktu w przedziale otwartym
; jednak nie ma takiego punktu w przedziale otwartym 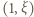 (nierówność (3)). W takim razie granicą tego ciągu musi być liczba 1.
(nierówność (3)). W takim razie granicą tego ciągu musi być liczba 1.
Funkcja ciągła 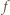 przeprowadza ten ciąg na ciąg rosnący
przeprowadza ten ciąg na ciąg rosnący 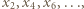 którego granicą jest wobec tego liczba
którego granicą jest wobec tego liczba 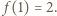 To dowodzi, że niezależnie od wyboru wyrazu początkowego
To dowodzi, że niezależnie od wyboru wyrazu początkowego 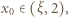 ciąg
ciąg 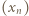 ma podciągi zbieżne do dwóch różnych granic: 1 oraz 2 (i do żadnej innej, bo dowolny podciąg ma nieskończenie wiele wspólnych wyrazów z jednym ze znalezionych podciągów, zbieżnych do 1 lub 2).
ma podciągi zbieżne do dwóch różnych granic: 1 oraz 2 (i do żadnej innej, bo dowolny podciąg ma nieskończenie wiele wspólnych wyrazów z jednym ze znalezionych podciągów, zbieżnych do 1 lub 2).
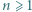 będzie liczbą całkowitą. Każdy
będzie liczbą całkowitą. Każdy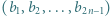 jest równy 1 lub -1. Parę
jest równy 1 lub -1. Parę 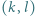 nazwiemy minusjedynkującą, jeśli
nazwiemy minusjedynkującą, jeśli 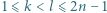 oraz
oraz 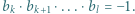 Wykazać, że liczba par
Wykazać, że liczba par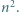
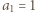
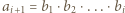
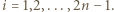
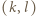
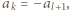
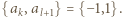
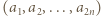
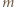
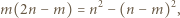
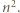
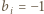
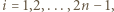
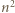
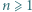
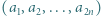
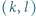
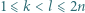
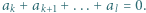
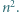
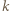
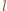
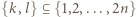
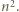
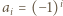
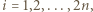
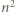
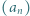 jest określony wzorami
jest określony wzorami 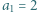 ;
; 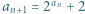 dla
dla 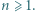 Niech
Niech 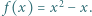 Udowodnić, że dla każdego
Udowodnić, że dla każdego 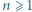 liczba
liczba 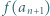 dzieli się przez
dzieli się przez 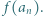
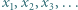 będzie rosnącym ciągiem wszystkich dodatnich liczb
będzie rosnącym ciągiem wszystkich dodatnich liczb 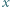 spełniających równanie
spełniających równanie 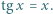 Niech
Niech 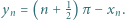 Obliczyć granicę ciągu
Obliczyć granicę ciągu 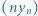 przy
przy 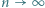 (lub wykazać, że granica nie istnieje).
(lub wykazać, że granica nie istnieje).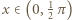 zachodzi nierówność
zachodzi nierówność 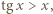 więc w tym przedziale nie leży żaden wyraz ciągu
więc w tym przedziale nie leży żaden wyraz ciągu 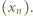 W każdym dalszym przedziale dodatniości funkcji tangens leży jeden wyraz. Tak więc
W każdym dalszym przedziale dodatniości funkcji tangens leży jeden wyraz. Tak więc 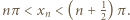 Wobec określenia
Wobec określenia 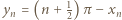 wynika stąd, że
wynika stąd, że 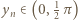 oraz
oraz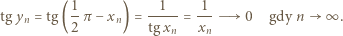
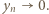 A skoro
A skoro 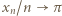 (oraz
(oraz 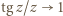 gdy
gdy 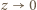 ), zatem
), zatem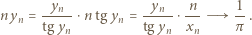
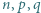 będą liczbami całkowitymi dodatnimi. Ciąg liczb całkowitych
będą liczbami całkowitymi dodatnimi. Ciąg liczb całkowitych 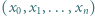 spełnia warunki:
spełnia warunki: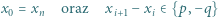
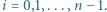 Udowodnić, że jeżeli
Udowodnić, że jeżeli 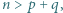 to istnieją takie
to istnieją takie 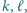 że
że 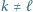 i
i 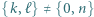 oraz
oraz 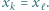
 będzie dowolną dodatnią liczbą nieparzystą. Spójrzmy na ciąg
będzie dowolną dodatnią liczbą nieparzystą. Spójrzmy na ciąg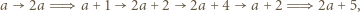
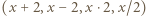 , zaś podwójna strzałka
, zaś podwójna strzałka 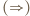 oznacza wielokrotne dodanie lub odjęcie dwójki, przebiegające monotonicznie przez wszystkie liczby tej samej parzystości, co liczby połączone tą podwójną strzałką. Na przykład dla
oznacza wielokrotne dodanie lub odjęcie dwójki, przebiegające monotonicznie przez wszystkie liczby tej samej parzystości, co liczby połączone tą podwójną strzałką. Na przykład dla 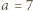 mamy ciąg
mamy ciąg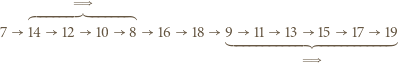
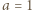 strzałka
strzałka 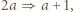 czyli
czyli 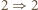 jest "pusta"). W tak określonym ciągu występują wszystkie liczby naturalne z przedziału
jest "pusta"). W tak określonym ciągu występują wszystkie liczby naturalne z przedziału ![|[a, 2a+ 5],](/math/temat/matematyka/teoria_liczb/zadania/2020/03/31/zm-k44-799/10x-22476a16ba6045895876a3c4680af4bf9c980bb5-im-66,57,43-FF,FF,FF.gif) każda jednorazowo.
każda jednorazowo.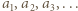 wzorem rekurencyjnym
wzorem rekurencyjnym 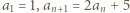 i zastosować podaną konstrukcję w każdym z przedziałów
i zastosować podaną konstrukcję w każdym z przedziałów ![[an,an+1].](/math/temat/matematyka/teoria_liczb/zadania/2020/03/31/zm-k44-799/3x-e1232ec1a01b8b6c5574063abc2b7eaab9e77fab-im-66,57,43-FF,FF,FF.gif)
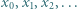 jest określony wzorami:
jest określony wzorami: 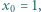

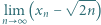 lub wykazać, że ta granica nie istnieje.
lub wykazać, że ta granica nie istnieje.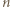 literką
literką 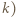 i dostajemy równoważną zależność
i dostajemy równoważną zależność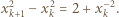
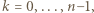 otrzymując
otrzymując
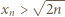 (dla
(dla 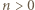 ), i wobec tego
), i wobec tego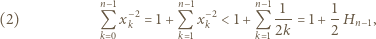
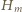 oznacza sumę odwrotności liczb naturalnych od 1 do
oznacza sumę odwrotności liczb naturalnych od 1 do  Zależności (1) i (2) dają oszacowanie
Zależności (1) i (2) dają oszacowanie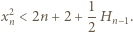
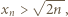 mamy stąd
mamy stąd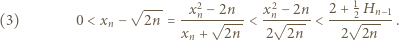
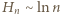 ; albo - bardziej elementarnie - z nierówności
; albo - bardziej elementarnie - z nierówności 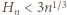 (nietrudnej do wykazania przez indukcję). Dwustronne oszacowanie (3) pokazuje, że
(nietrudnej do wykazania przez indukcję). Dwustronne oszacowanie (3) pokazuje, że 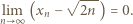
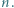 Ile ciągów
Ile ciągów 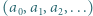 o wyrazach w zbiorze
o wyrazach w zbiorze 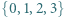 spełnia równość
spełnia równość 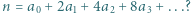
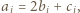 gdzie
gdzie 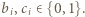 Ciągi
Ciągi 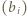 i
i 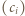 odpowiadają rozwinięciom dwójkowym liczb
odpowiadają rozwinięciom dwójkowym liczb 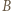 i
i 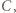 które spełniają równość
które spełniają równość 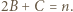
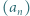 liczb naturalnych spełnia warunki
liczb naturalnych spełnia warunki 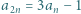 i
i 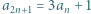 dla wszystkich naturalnych
dla wszystkich naturalnych 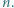 Dowieść, że jest to ciąg rosnący.
Dowieść, że jest to ciąg rosnący.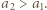 Załóżmy indukcyjnie, przy ustalonym
Załóżmy indukcyjnie, przy ustalonym 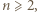 że
że 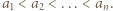 Trzeba dowieść, że
Trzeba dowieść, że 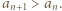 Należy tu rozważyć dwa przypadki:
Należy tu rozważyć dwa przypadki: 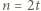 oraz
oraz 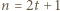 dla pewnego całkowitego dodatniego
dla pewnego całkowitego dodatniego 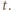 Pierwszy przypadek jest natychmiastowy i nie wymaga nawet skorzystania z założenia indukcyjnego. W drugim korzystamy z nierówności
Pierwszy przypadek jest natychmiastowy i nie wymaga nawet skorzystania z założenia indukcyjnego. W drugim korzystamy z nierówności 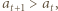 którą zapiszemy w postaci
którą zapiszemy w postaci 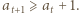
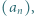 który spełnia warunki:
który spełnia warunki:

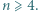
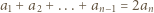
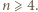 Z tego trzeba wywnioskować równość
Z tego trzeba wywnioskować równość 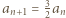 dla wszystkich
dla wszystkich 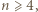 a to prowadzi do sprzeczności.
a to prowadzi do sprzeczności.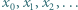 jest określony wzorem rekurencyjnym
jest określony wzorem rekurencyjnym 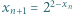 dla
dla 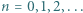 ; wyraz początkowy
; wyraz początkowy 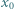 jest dowolną liczbą z przedziału
jest dowolną liczbą z przedziału 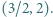 Wyznaczyć wszystkie liczby, będące granicami zbieżnych podciągów ciągu
Wyznaczyć wszystkie liczby, będące granicami zbieżnych podciągów ciągu 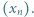
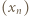 powstaje przez iterowanie funkcji
powstaje przez iterowanie funkcji 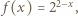 którą będziemy badać na przedziale
którą będziemy badać na przedziale ![[1,2].](/math/temat/matematyka/analiza/zadania/2018/03/25/zm-k44-759/3x-a051a26225a4472d5acd2ead6f6a678d0abff009-im-66,57,43-FF,FF,FF.gif) Ponieważ
Ponieważ 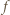 maleje od wartości
maleje od wartości 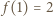 do wartości
do wartości 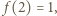 zatem odwzorowuje przedział
zatem odwzorowuje przedział ![[1,2]](/math/temat/matematyka/analiza/zadania/2018/03/25/zm-k44-759/7x-a051a26225a4472d5acd2ead6f6a678d0abff009-im-66,57,43-FF,FF,FF.gif) na siebie i ma w tym przedziale dokładnie jeden punkt stały
na siebie i ma w tym przedziale dokładnie jeden punkt stały 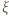 (tj. taki, że
(tj. taki, że 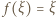 ). Obrazem przedziału
). Obrazem przedziału 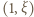 jest przedział
jest przedział 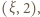 i na odwrót. Stąd wniosek, że wyrazy ciągu
i na odwrót. Stąd wniosek, że wyrazy ciągu 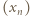 o numerach parzystych należą do jednego z tych przedziałów, a te o nieparzystych - do drugiego.
o numerach parzystych należą do jednego z tych przedziałów, a te o nieparzystych - do drugiego.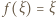 przepisujemy jako
przepisujemy jako 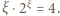 Funkcja
Funkcja 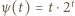 jest rosnąca; przy tym
jest rosnąca; przy tym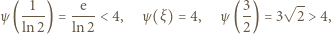
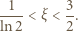
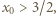 zatem
zatem 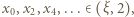 zaś
zaś 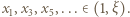
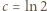 i zauważmy, że
i zauważmy, że 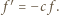 Niech
Niech 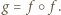 Wówczas
Wówczas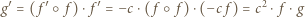
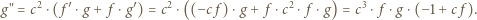
![x ∈ [1,ξ]](/math/temat/matematyka/analiza/zadania/2018/03/25/zm-k44-759/1x-ebb224189cbd9ab5aa439f6248ce3382f71c3782-im-66,57,43-FF,FF,FF.gif) mamy nierówność
mamy nierówność 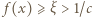 (por. (1)), więc wyrażenie w nawiasie po prawej stronie (2) ma w tych punktach wartość dodatnią. To znaczy, że funkcja
(por. (1)), więc wyrażenie w nawiasie po prawej stronie (2) ma w tych punktach wartość dodatnią. To znaczy, że funkcja 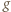 jest ściśle wypukła w przedziale
jest ściśle wypukła w przedziale ![|[1,ξ]](/math/temat/matematyka/analiza/zadania/2018/03/25/zm-k44-759/4x-ebb224189cbd9ab5aa439f6248ce3382f71c3782-im-66,57,43-FF,FF,FF.gif) ; a ponieważ
; a ponieważ 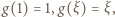 zatem
zatem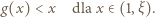
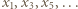 leży w przedziale
leży w przedziale 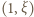 i jest generowany rekurencyjnie wzorem
i jest generowany rekurencyjnie wzorem 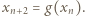 Nierówność (3) pokazuje, że jest to ciąg malejący, i w konsekwencji zbieżny. Jego granica musi być punktem stałym funkcji
Nierówność (3) pokazuje, że jest to ciąg malejący, i w konsekwencji zbieżny. Jego granica musi być punktem stałym funkcji 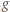 ; jednak nie ma takiego punktu w przedziale otwartym
; jednak nie ma takiego punktu w przedziale otwartym 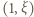 (nierówność (3)). W takim razie granicą tego ciągu musi być liczba 1.
(nierówność (3)). W takim razie granicą tego ciągu musi być liczba 1.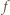 przeprowadza ten ciąg na ciąg rosnący
przeprowadza ten ciąg na ciąg rosnący 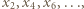 którego granicą jest wobec tego liczba
którego granicą jest wobec tego liczba 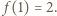 To dowodzi, że niezależnie od wyboru wyrazu początkowego
To dowodzi, że niezależnie od wyboru wyrazu początkowego 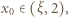 ciąg
ciąg 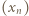 ma podciągi zbieżne do dwóch różnych granic: 1 oraz 2 (i do żadnej innej, bo dowolny podciąg ma nieskończenie wiele wspólnych wyrazów z jednym ze znalezionych podciągów, zbieżnych do 1 lub 2).
ma podciągi zbieżne do dwóch różnych granic: 1 oraz 2 (i do żadnej innej, bo dowolny podciąg ma nieskończenie wiele wspólnych wyrazów z jednym ze znalezionych podciągów, zbieżnych do 1 lub 2).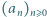 definiujemy rekurencyjnie:
definiujemy rekurencyjnie: 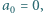
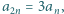
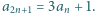 Scharakteryzuj wszystkie liczby całkowite
Scharakteryzuj wszystkie liczby całkowite 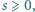 dla których istnieje dokładnie jedna para
dla których istnieje dokładnie jedna para 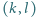 spełniająca warunki
spełniająca warunki 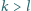 oraz
oraz 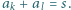
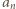 należy zapisać liczbę
należy zapisać liczbę 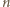 w systemie dwójkowym i odczytać w trójkowym.
w systemie dwójkowym i odczytać w trójkowym.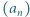 zadany przez
zadany przez 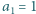 oraz
oraz 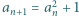 dla
dla 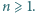 Rozstrzygnąć, czy istnieje dodatnia liczba całkowita
Rozstrzygnąć, czy istnieje dodatnia liczba całkowita 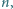 dla której
dla której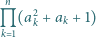
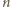 nie istnieje.
nie istnieje.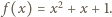 Bezpośrednio sprawdzamy, że dla dowolnego
Bezpośrednio sprawdzamy, że dla dowolnego 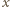 zachodzi równość
zachodzi równość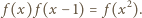
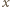 jest dodatnią liczbą całkowitą, to
jest dodatnią liczbą całkowitą, to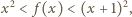
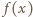 nie jest kwadratem liczby całkowitej.
nie jest kwadratem liczby całkowitej.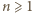 zachodzi równość
zachodzi równość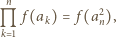
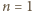 równość
równość 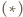 jest spełniona. Przypuśćmy, że zachodzi ona dla pewnego
jest spełniona. Przypuśćmy, że zachodzi ona dla pewnego 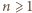 ; wówczas
; wówczas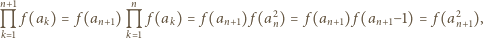
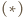 zachodzi również dla
zachodzi również dla 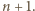 To kończy rozwiązanie.
To kończy rozwiązanie.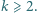 Czy istnieje rosnący ciąg liczb naturalnych
Czy istnieje rosnący ciąg liczb naturalnych 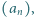 którego żaden wyraz ani żadna suma skończenie wielu jego wyrazów nie jest
którego żaden wyraz ani żadna suma skończenie wielu jego wyrazów nie jest 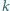 -tą potęgą liczby naturalnej, a przy tym ciąg
-tą potęgą liczby naturalnej, a przy tym ciąg 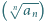 jest ograniczony?
jest ograniczony?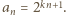
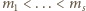 :
: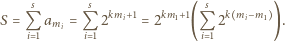
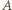 zachodziła równość
zachodziła równość 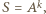 wówczas pisząc
wówczas pisząc 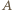 w postaci
w postaci 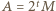 (
( 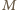 nieparzyste) i przyrównując potęgi dwójki w
nieparzyste) i przyrównując potęgi dwójki w 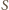 i w
i w 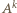 uzyskalibyśmy równość
uzyskalibyśmy równość 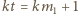 ; oczywista sprzeczność.
; oczywista sprzeczność.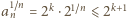 jest ograniczony.
jest ograniczony.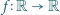 o następujących własnościach:
o następujących własnościach: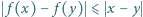 dla
dla 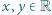 ;
;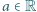 ciąg
ciąg 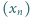 określony wzorami
określony wzorami 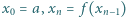 (dla
(dla 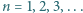 ) jest ciągiem arytmetycznym.
) jest ciągiem arytmetycznym.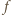 będzie funkcją, spełniającą postawione warunki, i przyjmijmy, że funkcja
będzie funkcją, spełniającą postawione warunki, i przyjmijmy, że funkcja 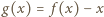 nie jest stała. Istnieją więc liczby
nie jest stała. Istnieją więc liczby 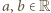 dla których
dla których 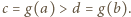 W drugim z warunków, podanych w zadaniu, przyjmujemy
W drugim z warunków, podanych w zadaniu, przyjmujemy 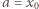 i tworzymy ciąg arytmetyczny
i tworzymy ciąg arytmetyczny 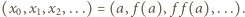 Skoro
Skoro 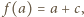 zatem
zatem 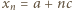 (dla wszystkich
(dla wszystkich  ). Jednocześnie
). Jednocześnie 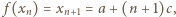 czyli
czyli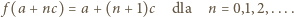
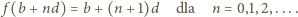
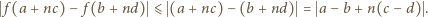
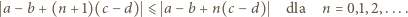
 wyrażenia ujęte w symbol wartości bezwzględnej mają wartość dodatnią (bo
wyrażenia ujęte w symbol wartości bezwzględnej mają wartość dodatnią (bo 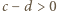 ). Można więc opuścić moduły. Ale zależność (3) - po skasowaniu modułów - redukuje się do postaci
). Można więc opuścić moduły. Ale zależność (3) - po skasowaniu modułów - redukuje się do postaci 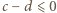 ; sprzeczność.
; sprzeczność.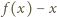 musi być stała. Jasne, że każda funkcja postaci
musi być stała. Jasne, że każda funkcja postaci 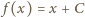 spełnia wymagane warunki.
spełnia wymagane warunki.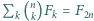 (
( 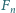 oznacza
oznacza  -tą liczbę Fibonacciego, czyli rozwiązanie równania rekurencyjnego
-tą liczbę Fibonacciego, czyli rozwiązanie równania rekurencyjnego 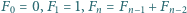 dla
dla 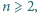 a zarazem liczbę pokryć paska
a zarazem liczbę pokryć paska 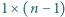 kwadratami
kwadratami 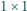 i prostokątami
i prostokątami 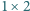 ).
).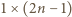 kwadratami
kwadratami 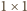 i prostokątami
i prostokątami 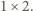 Każde takie pokrycie musi zawierać co najmniej
Każde takie pokrycie musi zawierać co najmniej 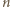 elementów, w tym co najmniej jeden kwadrat. Jeśli w pokryciu wśród pierwszych
elementów, w tym co najmniej jeden kwadrat. Jeśli w pokryciu wśród pierwszych 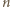 elementów jest dokładnie
elementów jest dokładnie 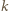 kwadratów (i
kwadratów (i 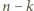 prostokątów
prostokątów 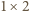 ), to można je rozmieścić na
), to można je rozmieścić na 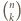 sposobów i pokrywają one w sumie prostokąt
sposobów i pokrywają one w sumie prostokąt 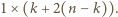 Pozostały fragment paska
Pozostały fragment paska 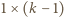 można pokryć na
można pokryć na 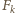 sposobów. Tę drugą interpretację opisuje lewa strona tożsamości, stąd teza.
sposobów. Tę drugą interpretację opisuje lewa strona tożsamości, stąd teza.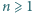 istnieje ciąg arytmetyczny
istnieje ciąg arytmetyczny  dodatnich liczb całkowitych, z których każda jest podzielna przez sumę swoich cyfr (w zapisie dziesiętnym).
dodatnich liczb całkowitych, z których każda jest podzielna przez sumę swoich cyfr (w zapisie dziesiętnym).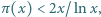 prawdziwego dla dostatecznie dużych
prawdziwego dla dostatecznie dużych 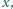 gdzie
gdzie 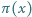 oznacza liczbę liczb pierwszych nie większych od
oznacza liczbę liczb pierwszych nie większych od 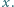
 będzie dodatnią liczbą całkowitą. Zauważmy, że każda mniejsza od
będzie dodatnią liczbą całkowitą. Zauważmy, że każda mniejsza od 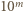 wielokrotność liczby
wielokrotność liczby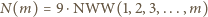
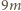 i podzielna przez
i podzielna przez 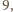 więc jest dzielnikiem liczby
więc jest dzielnikiem liczby 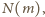 a tym bardziej dowolnej jej wielokrotności.
a tym bardziej dowolnej jej wielokrotności.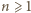 można dobrać takie
można dobrać takie 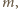 aby spełniona była nierówność
aby spełniona była nierówność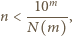
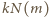 dla
dla 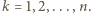
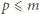 wchodzi do rozkładu liczby
wchodzi do rozkładu liczby 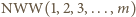 na czynniki pierwsze z wykładnikiem
na czynniki pierwsze z wykładnikiem 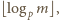 a zatem nie większym od
a zatem nie większym od 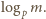 Wobec tego
Wobec tego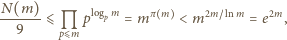
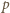 oraz skorzystaliśmy z nierówności zasugerowanej we wskazówce do zadania (prawdziwej dla
oraz skorzystaliśmy z nierówności zasugerowanej we wskazówce do zadania (prawdziwej dla 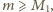 gdzie
gdzie 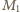 jest pewną dodatnią liczbą całkowitą).
jest pewną dodatnią liczbą całkowitą).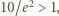 więc
więc 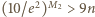 dla pewnej dodatniej liczby całkowitej
dla pewnej dodatniej liczby całkowitej 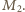 Do zakończenia rozwiązania wystarczy przyjąć
Do zakończenia rozwiązania wystarczy przyjąć 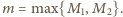
 Nie rozstrzyga ono jednak, czy istnieją dowolne długie ciągi arytmetyczne liczb naturalnych, które są podzielne przez sumę swoich cyfr w zapisie dwójkowym.
Nie rozstrzyga ono jednak, czy istnieją dowolne długie ciągi arytmetyczne liczb naturalnych, które są podzielne przez sumę swoich cyfr w zapisie dwójkowym.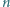 cyfr, piszemy łącznie
cyfr, piszemy łącznie 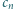 cyfr (np.
cyfr (np. 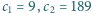 ); w tym
); w tym 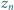 zer (np.
zer (np. 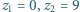 ). Czy równość
). Czy równość 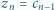 jest spełniona dla wszystkich liczb naturalnych
jest spełniona dla wszystkich liczb naturalnych 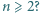
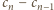 to liczba cyfr użytych do zapisania wszystkich liczb
to liczba cyfr użytych do zapisania wszystkich liczb  -cyfrowych. Jest tych liczb
-cyfrowych. Jest tych liczb 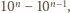 czyli
czyli 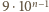 ; zatem
; zatem 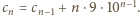 W zapisie każdej z nich cyfra wiodąca jest różna od zera; po jej odrzuceniu, pozostała część zapisu to dowolny ciąg długości
W zapisie każdej z nich cyfra wiodąca jest różna od zera; po jej odrzuceniu, pozostała część zapisu to dowolny ciąg długości 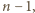 złożony z dowolnych cyfr (formalnie - słowo z alfabetu 10-elementowego).
złożony z dowolnych cyfr (formalnie - słowo z alfabetu 10-elementowego).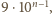 jest w nich więc
jest w nich więc 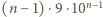 cyfr, a wszystkie cyfry są równouprawnione. Dziesiąta część spośród nich to zera. To znaczy, że w zapisie wszystkich liczb
cyfr, a wszystkie cyfry są równouprawnione. Dziesiąta część spośród nich to zera. To znaczy, że w zapisie wszystkich liczb 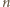 -cyfrowych mamy
-cyfrowych mamy 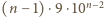 zer. Tak więc
zer. Tak więc 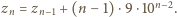 Pisząc
Pisząc 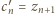 widzimy, że ciągi
widzimy, że ciągi 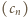 i
i 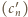 spełniają identyczną zależność rekurencyjną. Ponieważ
spełniają identyczną zależność rekurencyjną. Ponieważ 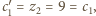 wynika stąd, że
wynika stąd, że 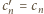 (dla
(dla 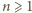 ), czyli
), czyli 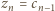 (dla
(dla 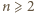 ).
).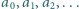 jest określony wzorem rekurencyjnym:
jest określony wzorem rekurencyjnym: 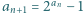 ; wyraz początkowy
; wyraz początkowy 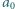 jest liczbą pierwszą. Dowieść, że dla każdego
jest liczbą pierwszą. Dowieść, że dla każdego 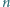 różnica
różnica 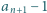 jest podzielna przez
jest podzielna przez 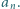
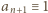 (mod
(mod 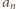 ) - po wprowadzeniu określenia liczby
) - po wprowadzeniu określenia liczby 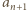 i dodaniu stronami jedynki - ma postać
i dodaniu stronami jedynki - ma postać
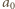 jest pierwsza, więc
jest pierwsza, więc 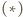 zachodzi dla
zachodzi dla 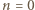 (małe twierdzenie Fermata). Dalej indukcja: przyjmijmy słuszność
(małe twierdzenie Fermata). Dalej indukcja: przyjmijmy słuszność 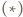 dla pewnego
dla pewnego 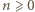 ; istnieje zatem liczba
; istnieje zatem liczba 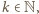 dla której
dla której 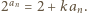 Odejmujemy stronami jedynkę i mamy
Odejmujemy stronami jedynkę i mamy 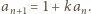 Z określenia
Z określenia 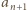 wynika ponadto, że
wynika ponadto, że 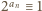 (mod
(mod 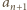 ). Tak więc
). Tak więc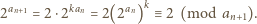
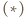 z
z 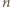 zastąpionym przez
zastąpionym przez 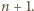 To kończy dowód indukcyjny.
To kończy dowód indukcyjny.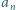 spełnia warunek
spełnia warunek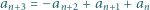
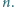 Znaleźć wartość
Znaleźć wartość 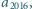 wiedząc, że
wiedząc, że 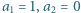 i
i 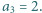
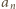 spełnia warunek
spełnia warunek 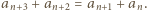 W takim razie
W takim razie