Klub 44F - zadania XI 2020»Zadanie 706
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44F - zadania XI 2020
- Publikacja w Delcie: listopad 2020
- Publikacja elektroniczna: 1 listopada 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (400 KB)
Gdy krótkowidz i dalekowidz używają swoich okularów, widzą tak jak człowiek, który ma dobry wzrok. Pewnego razu przez pomyłkę panowie zamienili swoje okulary. Po włożeniu okularów krótkowidza dalekowidz stwierdził, że widzi ostro tylko bardzo daleko położone przedmioty. Jaka jest najmniejsza odległość, z której krótkowidz w okularach dalekowidza widzi ostro drobny druk?
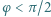
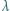 mieszczących się w zakresie
mieszczących się w zakresie 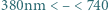 nm. Ile linii widma wodoru człowiek może zaobserwować bezpośrednio? Stała Plancka wynosi
nm. Ile linii widma wodoru człowiek może zaobserwować bezpośrednio? Stała Plancka wynosi 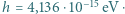 s, prędkość światła
s, prędkość światła 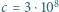 m/s, a stała Rydberga
m/s, a stała Rydberga 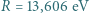 .
.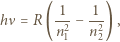
 oznacza częstość fali, a
oznacza częstość fali, a 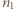 i
i 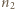 to numery poziomów energetycznych, między którymi zaszło przejście promieniste
to numery poziomów energetycznych, między którymi zaszło przejście promieniste 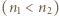 . Częstość
. Częstość  promieniowania związana jest z długością fali wzorem
promieniowania związana jest z długością fali wzorem 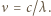 Zakres długości fal rejestrowanych przez ludzkie oko odpowiada więc zakresowi energii
Zakres długości fal rejestrowanych przez ludzkie oko odpowiada więc zakresowi energii 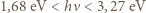 . Jeśli wyrazimy otrzymany zakres energii za pomocą stałej Rydberga, to otrzymamy
. Jeśli wyrazimy otrzymany zakres energii za pomocą stałej Rydberga, to otrzymamy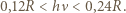
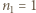 odpowiadają energiom większym od górnej granicy przedziału widzialnego, a na poziom
odpowiadają energiom większym od górnej granicy przedziału widzialnego, a na poziom 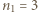 energiom mniejszym od dolnej granicy tego obszaru
energiom mniejszym od dolnej granicy tego obszaru 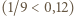 . W badanym obszarze znajdują się linie o
. W badanym obszarze znajdują się linie o 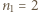 i
i 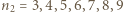 (ostatnie trzy linie wypadają w obszarze promieniowania nadfioletowego - za jego granicę przyjmuje się
(ostatnie trzy linie wypadają w obszarze promieniowania nadfioletowego - za jego granicę przyjmuje się 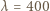 nm). Jest to tak zwana seria Balmera.
nm). Jest to tak zwana seria Balmera.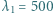 nm oraz
nm oraz 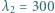 nm. W obu przypadkach strumień energii światła padającego na katodę był taki sam i wynosił
nm. W obu przypadkach strumień energii światła padającego na katodę był taki sam i wynosił 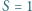 W/m
W/m 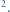 Jakie wartości napięcia hamowania i prądu nasycenia uzyskano dla każdej z użytych długości fal? Dla cezu praca wyjścia
Jakie wartości napięcia hamowania i prądu nasycenia uzyskano dla każdej z użytych długości fal? Dla cezu praca wyjścia 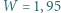
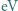 . Iloczyn stałej Plancka
. Iloczyn stałej Plancka 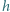 i prędkości światła
i prędkości światła 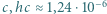 m, a ładunek elementarny
m, a ładunek elementarny 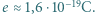
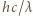 i maksymalna energia kinetyczna elektronów wybijanych z katody
i maksymalna energia kinetyczna elektronów wybijanych z katody 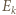 spełniają związek:
spełniają związek: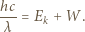
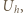 do którego pokonania nie wystarczy maksymalna energia kinetyczna uzyskiwana przez elektrony, całkowicie wygasza prąd przez fotokomórkę. Mamy więc:
do którego pokonania nie wystarczy maksymalna energia kinetyczna uzyskiwana przez elektrony, całkowicie wygasza prąd przez fotokomórkę. Mamy więc: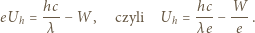
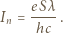
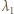 i
i 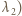 :
: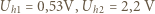
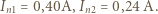
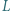 policjant będzie jeszcze mógł odczytać numer rejestracyjny pojazdu, jeśli wykona zdjęcie w świetle widzialnym za pomocą teleskopu Hubble'a o średnicy zwierciadła
policjant będzie jeszcze mógł odczytać numer rejestracyjny pojazdu, jeśli wykona zdjęcie w świetle widzialnym za pomocą teleskopu Hubble'a o średnicy zwierciadła 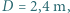 a tablice rejestracyjne będą miały taką formę jak dzisiaj.
a tablice rejestracyjne będą miały taką formę jak dzisiaj.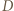 i fali o długości
i fali o długości 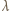 wynosi
wynosi 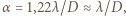 gdzie
gdzie 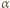 oznacza najmniejszy kąt tworzony przez kierunki, pod jakimi widzimy dwa punkty jako rozdzielone. Będzie to więc kąt, pod jakim widzimy najmniejsze rozróżnialne szczegóły o wielkości
oznacza najmniejszy kąt tworzony przez kierunki, pod jakimi widzimy dwa punkty jako rozdzielone. Będzie to więc kąt, pod jakim widzimy najmniejsze rozróżnialne szczegóły o wielkości 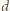 z odległości
z odległości 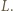 Światło widzialne odpowiada długościom fal świetlnych z przedziału od 380 do 770 nm. Do oszacowania przyjmijmy
Światło widzialne odpowiada długościom fal świetlnych z przedziału od 380 do 770 nm. Do oszacowania przyjmijmy 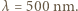 Jak się wydaje, do odczytania tablicy rejestracyjnej wystarczy rozróżnianie szczegółów o wielkości
Jak się wydaje, do odczytania tablicy rejestracyjnej wystarczy rozróżnianie szczegółów o wielkości 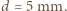 Mamy więc:
Mamy więc: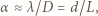
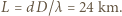
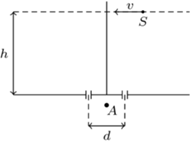
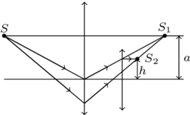
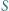 porusza się ruchem jednostajnym równolegle do ekranu, w którym znajdują się dwa małe otworki w odległości
porusza się ruchem jednostajnym równolegle do ekranu, w którym znajdują się dwa małe otworki w odległości 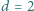 mm od siebie. Odległość źródła od ekranu wynosi
mm od siebie. Odległość źródła od ekranu wynosi 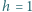 m. Oświetlenie w punkcie
m. Oświetlenie w punkcie 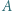 na osi układu zmienia się z częstotliwością
na osi układu zmienia się z częstotliwością 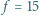 Hz, długość fali świetlnej emitowanej przez źródło
Hz, długość fali świetlnej emitowanej przez źródło 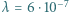 m. Znaleźć prędkość źródła
m. Znaleźć prędkość źródła 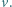 Podczas pomiarów oświetlenia źródło znajduje się w małej odległości od osi układu.
Podczas pomiarów oświetlenia źródło znajduje się w małej odległości od osi układu.
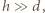 różnica dróg promieni docierających ze źródła do punktu
różnica dróg promieni docierających ze źródła do punktu 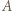 po ugięciu na dwóch szczelinach wynosi
po ugięciu na dwóch szczelinach wynosi 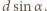 Maksimum oświetlenia rejestrujemy, gdy
Maksimum oświetlenia rejestrujemy, gdy 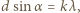 gdzie
gdzie 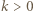 jest liczbą całkowitą. Odległość źródła
jest liczbą całkowitą. Odległość źródła 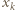 od osi układu jest mała, możemy więc stosować przybliżenie małych kątów:
od osi układu jest mała, możemy więc stosować przybliżenie małych kątów: 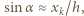 stąd
stąd 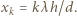 Droga przebyta przez źródło w czasie równym okresowi zmian oświetlenia punktu
Droga przebyta przez źródło w czasie równym okresowi zmian oświetlenia punktu 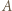 wynosi
wynosi 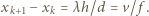 Po podstawieniu danych liczbowych otrzymujemy
Po podstawieniu danych liczbowych otrzymujemy 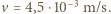
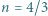 jest mniejszy od współczynnika załamania szkła. Jaka może być najmniejsza grubość tej warstwy, aby przy prostopadłym padaniu światła białego długości fali
jest mniejszy od współczynnika załamania szkła. Jaka może być najmniejsza grubość tej warstwy, aby przy prostopadłym padaniu światła białego długości fali 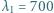 nm oraz
nm oraz 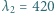 nm w świetle odbitym były jednocześnie maksymalnie wygaszone?
nm w świetle odbitym były jednocześnie maksymalnie wygaszone?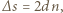 gdzie
gdzie 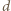 jest grubością warstwy. Oba promienie odbijają się od ośrodka gęstszego optycznie, warunki na minima interferencyjne dla obu długości fal mają więc postać:
jest grubością warstwy. Oba promienie odbijają się od ośrodka gęstszego optycznie, warunki na minima interferencyjne dla obu długości fal mają więc postać: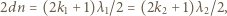
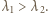 Stąd:
Stąd: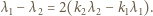
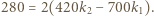 Najmniejsze liczby całkowite nieujemne spełniające to równanie to
Najmniejsze liczby całkowite nieujemne spełniające to równanie to 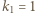 ,
, 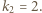 Szukana grubość warstwy
Szukana grubość warstwy 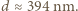
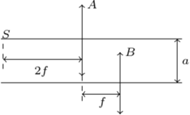
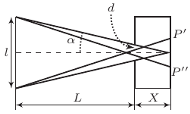
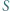 i jego obrazem w układzie optycznym przedstawionym na rysunku. Ogniskowe soczewek
i jego obrazem w układzie optycznym przedstawionym na rysunku. Ogniskowe soczewek 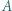 i
i 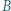 są jednakowe i równe
są jednakowe i równe 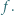
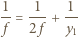
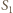 w pierwszej soczewce
w pierwszej soczewce 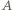 powstaje w odległości
powstaje w odległości 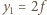 od tej soczewki. Obraz ten jest przedmiotem pozornym dla soczewki
od tej soczewki. Obraz ten jest przedmiotem pozornym dla soczewki 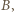 położonym w
położonym w 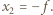 Oznaczając przez
Oznaczając przez 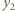 odległość obrazu
odległość obrazu 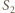 od drugiej soczewki po przejściu światła przez układ, otrzymujemy ze wzoru soczewkowego:
od drugiej soczewki po przejściu światła przez układ, otrzymujemy ze wzoru soczewkowego: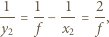
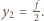 Odległość
Odległość 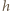 punktu
punktu 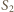 od osi optycznej drugiej soczewki wynika ze wzoru na powiększenie:
od osi optycznej drugiej soczewki wynika ze wzoru na powiększenie: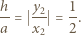
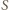 i obrazem
i obrazem 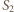 wynosi
wynosi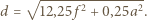
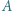 i
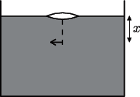
i 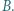 Odległości źródeł od kartki dobieramy tak, aby (przy prostopadłej obserwacji) zniknęła różnica jasności plamy i reszty kartki. Wówczas natężenia światła źródeł mają się do siebie, w przybliżeniu, jak kwadraty ich odległości od kartki:
Odległości źródeł od kartki dobieramy tak, aby (przy prostopadłej obserwacji) zniknęła różnica jasności plamy i reszty kartki. Wówczas natężenia światła źródeł mają się do siebie, w przybliżeniu, jak kwadraty ich odległości od kartki: 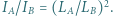 Wspomniane przybliżenie polega na założeniu, że tłusta plama przepuszcza całe padające na nią światło, a reszta kartki całkowicie je odbija. Jak należy zmodyfikować metodę pomiaru, żeby uzyskać poprawną wartość
Wspomniane przybliżenie polega na założeniu, że tłusta plama przepuszcza całe padające na nią światło, a reszta kartki całkowicie je odbija. Jak należy zmodyfikować metodę pomiaru, żeby uzyskać poprawną wartość 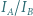 bez tego założenia?
bez tego założenia?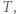 a odbicia
a odbicia 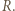 Niech dla reszty kartki odpowiednie współczynniki wynoszą
Niech dla reszty kartki odpowiednie współczynniki wynoszą  i
i 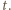 Plama "znika", gdy źródło
Plama "znika", gdy źródło 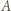 jest w odległości
jest w odległości 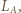 a źródło
a źródło 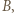 w odległości
w odległości 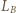 od kartki (patrzymy od strony
od kartki (patrzymy od strony 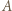 ). Mamy wówczas (oświetlenia obu części kartki są równe):
). Mamy wówczas (oświetlenia obu części kartki są równe):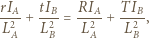
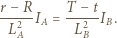
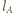 i
i 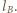 Otrzymujemy analogiczne równania (
Otrzymujemy analogiczne równania ( 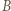 jest teraz od strony obserwatora):
jest teraz od strony obserwatora):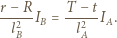
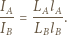
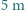 od niego. Jeden obraz znajduje się w odległości
od niego. Jeden obraz znajduje się w odległości 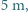 drugi w odległości
drugi w odległości 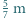 od nauczyciela. Po odwróceniu do klasy nauczyciel widzi przez okulary obraz tego samego ucznia w odległości
od nauczyciela. Po odwróceniu do klasy nauczyciel widzi przez okulary obraz tego samego ucznia w odległości 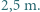 Wyznaczyć współczynnik załamania szkła, z którego wykonane są soczewki okularów.
Wyznaczyć współczynnik załamania szkła, z którego wykonane są soczewki okularów.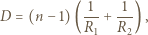
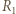 i
i 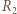 są promieniami krzywizny powierzchni soczewki. Są one dodatnie, gdy powierzchnia soczewki jest wypukła, i ujemne, gdy powierzchnia jest wklęsła. Odległość ucznia od soczewki jest stała i wynosi
są promieniami krzywizny powierzchni soczewki. Są one dodatnie, gdy powierzchnia soczewki jest wypukła, i ujemne, gdy powierzchnia jest wklęsła. Odległość ucznia od soczewki jest stała i wynosi 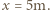 Gdy nauczyciel patrzy na ucznia przez okulary, widzi jego obraz pozorny w odległości
Gdy nauczyciel patrzy na ucznia przez okulary, widzi jego obraz pozorny w odległości 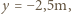 stąd
stąd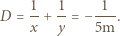
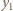 powstaje w wyniku odbicia od powierzchni soczewki bliższej oka. Zdolność skupiająca takiego zwierciadła wynosi
powstaje w wyniku odbicia od powierzchni soczewki bliższej oka. Zdolność skupiająca takiego zwierciadła wynosi 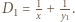 Musimy rozważyć dwa przypadki:
Musimy rozważyć dwa przypadki: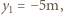
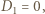 powierzchnia soczewki jest płaska,
powierzchnia soczewki jest płaska,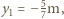
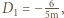 powierzchnia jest wypukła, czyli
powierzchnia jest wypukła, czyli 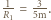
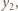 powstaje w wyniku przejścia światła przez soczewkę, odbiciu od powierzchni o zdolności skupiającej
powstaje w wyniku przejścia światła przez soczewkę, odbiciu od powierzchni o zdolności skupiającej 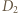 dalszej od oka i ponownym przejściu przez soczewkę. Zdolność skupiająca takiego układu wynosi
dalszej od oka i ponownym przejściu przez soczewkę. Zdolność skupiająca takiego układu wynosi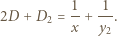
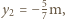
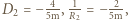
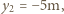
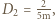
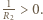
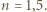
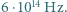 Znaleźć częstość światła padającego na wykonaną z tego metalu fotokatodę, jeżeli emitowane z jej powierzchni fotoelektrony można całkowicie zatrzymać, umieszczając przed nią siatkę, mającą w stosunku do niej potencjał
Znaleźć częstość światła padającego na wykonaną z tego metalu fotokatodę, jeżeli emitowane z jej powierzchni fotoelektrony można całkowicie zatrzymać, umieszczając przed nią siatkę, mającą w stosunku do niej potencjał 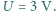
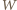 elektronu, charakterystyczną dla metalu, z którego zrobiona jest fotokatoda:
elektronu, charakterystyczną dla metalu, z którego zrobiona jest fotokatoda: 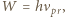 gdzie
gdzie 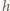 to stała Plancka. W rozpatrywanym przypadku
to stała Plancka. W rozpatrywanym przypadku 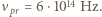 Skoro siatka, mająca potencjał
Skoro siatka, mająca potencjał 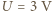 zatrzymuje wszystkie fotoelektrony, to ich energia kinetyczna
zatrzymuje wszystkie fotoelektrony, to ich energia kinetyczna 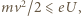 gdzie
gdzie 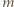 i
i  to masa i ładunek elektronu, a
to masa i ładunek elektronu, a  - jego prędkość, przy czym znak równości odpowiada elektronom o maksymalnej prędkości
- jego prędkość, przy czym znak równości odpowiada elektronom o maksymalnej prędkości 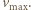 Energia, potrzebna do wykonania pracy wyjścia i nadania elektronowi prędkości, pochodzi od fotonu o częstości
Energia, potrzebna do wykonania pracy wyjścia i nadania elektronowi prędkości, pochodzi od fotonu o częstości 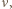 więc zgodnie z prawem zachowania energii mamy
więc zgodnie z prawem zachowania energii mamy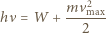
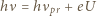
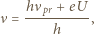
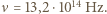
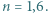 Promień powierzchni wypukłej wynosi
Promień powierzchni wypukłej wynosi 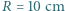 , grubość soczewki
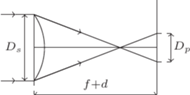
, grubość soczewki 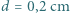 . Na powierzchnię płaską soczewki pada równolegle do jej osi optycznej wiązka światła. Gdy odsłonięta jest tylko niewielka część soczewki wokół osi optycznej, promienie ogniskują się na ekranie. Znaleźć średnicę plamki na ekranie po odsłonięciu całej soczewki.
. Na powierzchnię płaską soczewki pada równolegle do jej osi optycznej wiązka światła. Gdy odsłonięta jest tylko niewielka część soczewki wokół osi optycznej, promienie ogniskują się na ekranie. Znaleźć średnicę plamki na ekranie po odsłonięciu całej soczewki.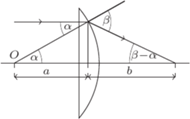
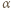 i załamuje się pod kątem
i załamuje się pod kątem 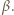 Odległość środka krzywizny
Odległość środka krzywizny 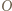 od punktu przecięcia promienia załamanego z osią optyczną soczewki wynosi
od punktu przecięcia promienia załamanego z osią optyczną soczewki wynosi 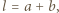 gdzie
gdzie 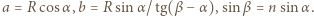 Podstawiając, otrzymujemy
Podstawiając, otrzymujemy
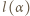 maleje ze wzrostem kąta
maleje ze wzrostem kąta 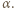 Gdy promień pada na koniec soczewki, kąt
Gdy promień pada na koniec soczewki, kąt 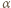 jest maksymalny i spełnia równanie
jest maksymalny i spełnia równanie 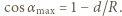 Dla podanych danych liczbowych maksymalny kąt
Dla podanych danych liczbowych maksymalny kąt 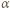 jest większy od kąta granicznego, zatem wszystkie promienie wiązki padające na soczewkę załamują się na jej powierzchni sferycznej. Skrajne promienie wiązki przecinają oś optyczną w odległości
jest większy od kąta granicznego, zatem wszystkie promienie wiązki padające na soczewkę załamują się na jej powierzchni sferycznej. Skrajne promienie wiązki przecinają oś optyczną w odległości 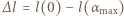 od ekranu. Zgodnie z (*),
od ekranu. Zgodnie z (*),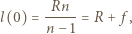
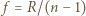 jest ogniskową cienkiej soczewki płaskowypukłej. Szukana średnica plamki na ekranie dana jest wzorem
jest ogniskową cienkiej soczewki płaskowypukłej. Szukana średnica plamki na ekranie dana jest wzorem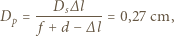
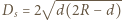 jest średnicą soczewki.
jest średnicą soczewki.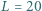 m. Jaką głębokość powinna mieć camera obscura z otworem o średnicy
m. Jaką głębokość powinna mieć camera obscura z otworem o średnicy 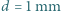 , aby na fotografii były widoczne pręgi na skórze tygrysa? Przyjąć, że odległość między pręgami wynosi
, aby na fotografii były widoczne pręgi na skórze tygrysa? Przyjąć, że odległość między pręgami wynosi 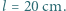
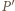 i
i 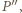 na które padają promienie pochodzące od najbliższych punktów sąsiednich pręg, nie mogą się przekrywać. Warunek ten będzie spełniony dla głębokości kamery
na które padają promienie pochodzące od najbliższych punktów sąsiednich pręg, nie mogą się przekrywać. Warunek ten będzie spełniony dla głębokości kamery 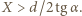 Ponieważ
Ponieważ 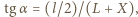 więc
więc 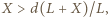 skąd
skąd 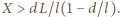 Korzystając z tego, że
Korzystając z tego, że 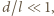 otrzymujemy
otrzymujemy 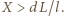 Tak więc głębokość kamery powinna być większa niż
Tak więc głębokość kamery powinna być większa niż 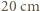 .
.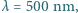 padająca prostopadle na płytkę, ogniskuje się w odległości
padająca prostopadle na płytkę, ogniskuje się w odległości 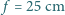 od płytki. Rozmiary płytki są małe w porównaniu z odległością
od płytki. Rozmiary płytki są małe w porównaniu z odległością 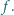
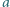 od płytki na jej osi przechodzącej przez środki pierścieni?
od płytki na jej osi przechodzącej przez środki pierścieni?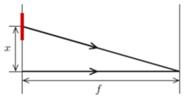
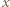 od centrum płytki do środka ekranu umieszczonego w odległości
od centrum płytki do środka ekranu umieszczonego w odległości 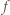 od płytki wynosi:
od płytki wynosi: 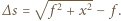 W przybliżeniu
W przybliżeniu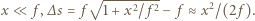
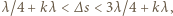 gdzie
gdzie 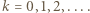 Stąd
Stąd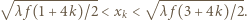
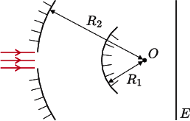
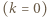 ma promień wewnętrzny
ma promień wewnętrzny 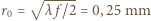 , zewnętrzny
, zewnętrzny 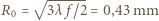 , drugi
, drugi 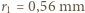 ,
, 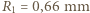 . b) niech szukana odległość wynosi
. b) niech szukana odległość wynosi 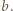 Chcemy, żeby różnica dróg promieni przechodzących przez punkt odległy o
Chcemy, żeby różnica dróg promieni przechodzących przez punkt odległy o  od środka płytki i przechodzących przez środek płytki była taka sama, jak w przypadku wiązki równoległej:
od środka płytki i przechodzących przez środek płytki była taka sama, jak w przypadku wiązki równoległej: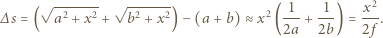
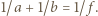
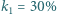 padającej na niego wiązki niespolaryzowanego światła, a dwa takie polaryzatory, ustawione jeden za drugim, przepuszczają
padającej na niego wiązki niespolaryzowanego światła, a dwa takie polaryzatory, ustawione jeden za drugim, przepuszczają 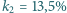 światła. Ile wynosi kąt
światła. Ile wynosi kąt  między płaszczyznami polaryzacji tych polaryzatorów?
między płaszczyznami polaryzacji tych polaryzatorów?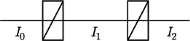
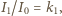 gdzie
gdzie 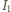 i
i 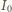 - natężenia wiązki padającej i przechodzącej dla pierwszego polaryzatora.
- natężenia wiązki padającej i przechodzącej dla pierwszego polaryzatora.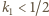 oznacza, że polaryzator częściowo pochłania światło. Jeżeli przepuszcza on, ze względu na pochłanianie, tylko
oznacza, że polaryzator częściowo pochłania światło. Jeżeli przepuszcza on, ze względu na pochłanianie, tylko 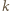 procent padającej wiązki, to
procent padającej wiązki, to 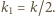 Gdy światło przechodzi przez dwa polaryzatory, to
Gdy światło przechodzi przez dwa polaryzatory, to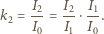
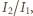 skorzystamy z prawa Malusa, które mówi, że natężenia światła spolaryzowanego padającego na polaryzator
skorzystamy z prawa Malusa, które mówi, że natężenia światła spolaryzowanego padającego na polaryzator 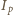 i z niego wychodzącego
i z niego wychodzącego 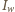 związane są wzorem
związane są wzorem 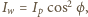 gdzie
gdzie 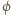 jest kątem między płaszczyzną polaryzacji światła padającego i płaszczyzną polaryzacji polaryzatora. Dodatkowo musimy uwzględnić to, że także w drugim polaryzatorze światło jest pochłaniane. Mamy więc:
jest kątem między płaszczyzną polaryzacji światła padającego i płaszczyzną polaryzacji polaryzatora. Dodatkowo musimy uwzględnić to, że także w drugim polaryzatorze światło jest pochłaniane. Mamy więc: 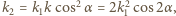 a stąd
a stąd 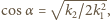 co daje
co daje 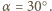
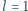 m doskonale odbijającą płytkę o masie
m doskonale odbijającą płytkę o masie 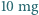 pada, prostopadle do jej powierzchni, wiązka światła laserowego. Jaka musiałaby być moc
pada, prostopadle do jej powierzchni, wiązka światła laserowego. Jaka musiałaby być moc 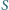 padającego światła, aby pod jego działaniem wahadło, którym jest zawieszona na nitce płytka, wychyliło się o kąt
padającego światła, aby pod jego działaniem wahadło, którym jest zawieszona na nitce płytka, wychyliło się o kąt 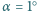 z położenia równowagi?
z położenia równowagi?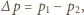 gdzie
gdzie 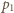 to pęd fotonu padającego, a
to pęd fotonu padającego, a 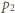 - pęd fotonu odbitego. Dla powierzchni doskonale odbijającej pędy
- pęd fotonu odbitego. Dla powierzchni doskonale odbijającej pędy 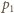 i
i 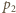 mają tę samą wartość
mają tę samą wartość 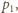 ale różnią się zwrotem, stąd zmiana pędu płytki wynosi
ale różnią się zwrotem, stąd zmiana pędu płytki wynosi 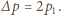 Energia
Energia 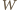 padających na płytkę w ciągu 1 s fotonów jest z definicji równa padającej na płytkę mocy
padających na płytkę w ciągu 1 s fotonów jest z definicji równa padającej na płytkę mocy 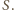 Ponieważ pęd
Ponieważ pęd 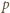 fotonu wiąże się z jego energią
fotonu wiąże się z jego energią 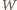 wzorem
wzorem 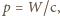 gdzie
gdzie  to prędkość światła, więc suma pędów fotonów padających na płytkę w czasie 1 s wynosi
to prędkość światła, więc suma pędów fotonów padających na płytkę w czasie 1 s wynosi 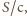 a pęd uzyskany przez płytkę w ciągu
a pęd uzyskany przez płytkę w ciągu 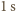 wynosi
wynosi 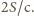 Zmiana pędu płytki w ciągu
Zmiana pędu płytki w ciągu 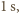 na mocy drugiej zasady dynamiki, jest równa działającej sile, więc
na mocy drugiej zasady dynamiki, jest równa działającej sile, więc 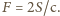 Ponieważ wychylenie wahadła wiąże się z siłą wzorem
Ponieważ wychylenie wahadła wiąże się z siłą wzorem 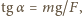 znajdujemy, że potrzebna moc to
znajdujemy, że potrzebna moc to 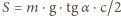 (przyjęliśmy, że dla
(przyjęliśmy, że dla 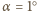 kąt padania wiązki nie zmienia się). Po podstawieniu danych liczbowych otrzymujemy
kąt padania wiązki nie zmienia się). Po podstawieniu danych liczbowych otrzymujemy 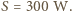 Dla wiązki światła laserowego o średnicy
Dla wiązki światła laserowego o średnicy 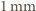 daje to gęstość mocy około
daje to gęstość mocy około 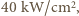 czyli z zakresu gęstości mocy stosowanych w technologiach cięcia i spawania metali.
czyli z zakresu gęstości mocy stosowanych w technologiach cięcia i spawania metali.
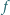 i zwierciadło sferyczne wklęsłe mają wspólną oś optyczną. Środek zwierciadła znajduje się w jednym z ognisk soczewki. Układ daje rzeczywisty obraz przedmiotu
i zwierciadło sferyczne wklęsłe mają wspólną oś optyczną. Środek zwierciadła znajduje się w jednym z ognisk soczewki. Układ daje rzeczywisty obraz przedmiotu 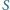 umieszczonego w dowolnej odległości na prawo od soczewki. Znaleźć ogniskową zwierciadła.
umieszczonego w dowolnej odległości na prawo od soczewki. Znaleźć ogniskową zwierciadła.
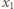 oznacza odległość przedmiotu
oznacza odległość przedmiotu 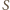 od soczewki. Zgodnie ze wzorem soczewkowym odległość obrazu od soczewki dana jest wzorem
od soczewki. Zgodnie ze wzorem soczewkowym odległość obrazu od soczewki dana jest wzorem 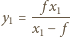 i dla przedmiotu rzeczywistego, gdy
i dla przedmiotu rzeczywistego, gdy 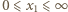 , spełnia warunki
, spełnia warunki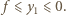
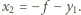 Zgodnie z (1)
Zgodnie z (1)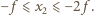
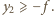 Soczewka rozpraszająca daje rzeczywisty obraz przedmiotu pozornego, gdy odległość tego przedmiotu
Soczewka rozpraszająca daje rzeczywisty obraz przedmiotu pozornego, gdy odległość tego przedmiotu 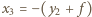 spełnia warunek
spełnia warunek 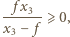 czyli
czyli 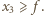 Stąd
Stąd 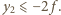 Zatem spełnione są warunki
Zatem spełnione są warunki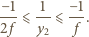
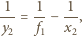
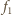 jest ogniskową zwierciadła, otrzymujemy następujące ograniczenia:
jest ogniskową zwierciadła, otrzymujemy następujące ograniczenia: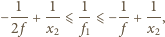
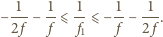
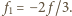
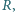 wykonana ze szkła o współczynniku załamania
wykonana ze szkła o współczynniku załamania 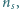 zanurzona jest jedną stroną w wodzie. Mały przedmiot znajduje się w wodzie na osi optycznej soczewki, w odległości
zanurzona jest jedną stroną w wodzie. Mały przedmiot znajduje się w wodzie na osi optycznej soczewki, w odległości 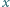 od soczewki. Wysokość przedmiotu wynosi
od soczewki. Wysokość przedmiotu wynosi 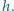 W soczewce powstaje obraz pozorny. Jakie jest jego powiększenie liniowe? Współczynnik załamania wody jest równy
W soczewce powstaje obraz pozorny. Jakie jest jego powiększenie liniowe? Współczynnik załamania wody jest równy 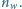
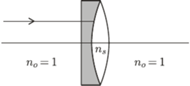
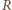 oraz płasko-wklęsłej soczewki wodnej (
oraz płasko-wklęsłej soczewki wodnej (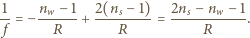
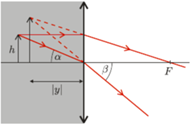
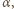 a kąt załamania tego promienia przez
a kąt załamania tego promienia przez 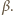 Ponieważ przedmiot jest mały, mamy
Ponieważ przedmiot jest mały, mamy 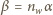 zgodnie z prawem załamania. Korzystając z
zgodnie z prawem załamania. Korzystając z 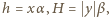 gdzie
gdzie 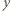 jest odległością obrazu od soczewki,
jest odległością obrazu od soczewki, 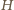 wysokością obrazu. Z podobieństwa odpowiednich trójkątów mamy też:
wysokością obrazu. Z podobieństwa odpowiednich trójkątów mamy też: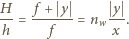
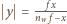 , a szukane powiększenie dane jest wzorem
, a szukane powiększenie dane jest wzorem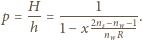
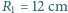 i
i 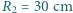 . Jaka jest ogniskowa cienkiej soczewki, za pomocą której można otrzymać obraz Słońca o takiej samej wielkości?
. Jaka jest ogniskowa cienkiej soczewki, za pomocą której można otrzymać obraz Słońca o takiej samej wielkości?
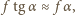 gdzie
gdzie 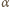 jest promieniem kątowym Słońca widzianego z Ziemi, a
jest promieniem kątowym Słońca widzianego z Ziemi, a 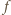 ogniskową soczewki albo zwierciadła. Obraz pozorny Słońca w zwierciadle wypukłym o ogniskowej
ogniskową soczewki albo zwierciadła. Obraz pozorny Słońca w zwierciadle wypukłym o ogniskowej 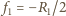 ma promień
ma promień 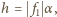 jest przedmiotem dla zwierciadła wklęsłego o ogniskowej
jest przedmiotem dla zwierciadła wklęsłego o ogniskowej 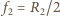 i znajduje się w odległości od niego równej
i znajduje się w odległości od niego równej 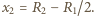 Obraz, który powstaje w zwierciadle wklęsłym, oddalony jest od niego o
Obraz, który powstaje w zwierciadle wklęsłym, oddalony jest od niego o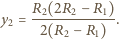
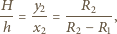
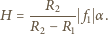
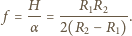
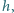 aby pływająca w tym jeziorze rybka nie mogła go zobaczyć? Powierzchnia wody jest idealnie płaska. Pomiń krzywiznę Ziemi.
aby pływająca w tym jeziorze rybka nie mogła go zobaczyć? Powierzchnia wody jest idealnie płaska. Pomiń krzywiznę Ziemi.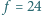 obrazy na sekundę sfilmowano drgania wahadła matematycznego. Jeden pełny okres wahań zajmuje
obrazy na sekundę sfilmowano drgania wahadła matematycznego. Jeden pełny okres wahań zajmuje 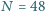 kadrów. Długość obrazu wahadła na kliszy filmowej wynosi
kadrów. Długość obrazu wahadła na kliszy filmowej wynosi 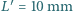 . Ogniskowa obiektywu kamery wynosi
. Ogniskowa obiektywu kamery wynosi 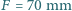 . Z jakiej odległości
. Z jakiej odległości 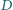 sfilmowano wahadło?
sfilmowano wahadło?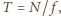 a stąd jego długość
a stąd jego długość 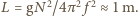 Długość obrazu wahadła jest więc znacznie mniejsza od jego długości rzeczywistej
Długość obrazu wahadła jest więc znacznie mniejsza od jego długości rzeczywistej 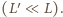 Oznacza to, że poszukiwana odległość
Oznacza to, że poszukiwana odległość 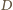 od kamery do wahadła wielokrotnie przewyższa ogniskową obiektywu
od kamery do wahadła wielokrotnie przewyższa ogniskową obiektywu 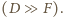 Stąd z kolei wynika, że obraz wahadła znajduje się bardzo blisko ogniska obiektywu, a więc odległość od obiektywu do kliszy, na której powstaje obraz, jest w przybliżeniu równa
Stąd z kolei wynika, że obraz wahadła znajduje się bardzo blisko ogniska obiektywu, a więc odległość od obiektywu do kliszy, na której powstaje obraz, jest w przybliżeniu równa 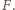 Stąd wynika, że
Stąd wynika, że 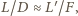 czyli
czyli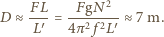
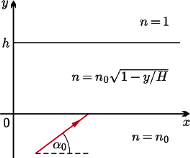
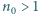 i
i 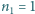 znajduje się warstwa ośrodka, w którym współczynnik załamania zmienia się zgodnie ze wzorem
znajduje się warstwa ośrodka, w którym współczynnik załamania zmienia się zgodnie ze wzorem 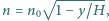 gdzie
gdzie 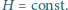 Grubość warstwy wynosi
Grubość warstwy wynosi 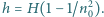 Z ośrodka o współczynniku załamania
Z ośrodka o współczynniku załamania 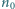 wpada do niejednorodnej warstwy promień światła. Dla jakich wartości kąta
wpada do niejednorodnej warstwy promień światła. Dla jakich wartości kąta 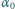 promień wróci do optycznie gęstszego ośrodka? Dla jakiej wartości tego kąta odległość między punktami wejścia i wyjścia promienia będzie największa?
promień wróci do optycznie gęstszego ośrodka? Dla jakiej wartości tego kąta odległość między punktami wejścia i wyjścia promienia będzie największa?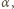 jaki tworzy styczna do toru z osią
jaki tworzy styczna do toru z osią 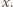 Zgodnie z prawem załamania zachodzi związek
Zgodnie z prawem załamania zachodzi związek 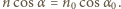 Rozważmy ruch punktu materialnego, którego prędkość wzdłuż granicy ośrodków jest stała:
Rozważmy ruch punktu materialnego, którego prędkość wzdłuż granicy ośrodków jest stała: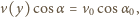
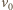 jest prędkością na granicy ośrodków, stąd
jest prędkością na granicy ośrodków, stąd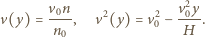
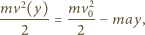
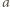 jest stałym przyspieszeniem cząstki i wynosi
jest stałym przyspieszeniem cząstki i wynosi 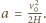 Korzystając ze wzorów dla rzutu ukośnego w polu stałej siły, otrzymujemy dla
Korzystając ze wzorów dla rzutu ukośnego w polu stałej siły, otrzymujemy dla 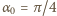 maksymalną odległość między punktami wejścia i wyjścia promienia z ośrodka niejednorodnego
maksymalną odległość między punktami wejścia i wyjścia promienia z ośrodka niejednorodnego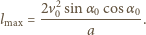
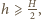 czyli
czyli 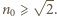 W przeciwnym przypadku odległość między punktami wejścia i wyjścia promienia odpowiada takiemu kątowi
W przeciwnym przypadku odległość między punktami wejścia i wyjścia promienia odpowiada takiemu kątowi 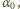 dla którego promień jest styczny do górnej granicy rozdziału ośrodków:
dla którego promień jest styczny do górnej granicy rozdziału ośrodków: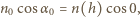
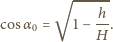
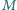 i prędkościach
i prędkościach 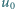 tworzą równoległą wiązkę. Wiązka ta zderza się z przeciwbieżną, monochromatyczną wiązką fotonów (światła laserowego) o energiach równych energii wzbudzenia atomów ze stanu podstawowego do jednego ze stanów wzbudzonych o naturalnym czasie życia
tworzą równoległą wiązkę. Wiązka ta zderza się z przeciwbieżną, monochromatyczną wiązką fotonów (światła laserowego) o energiach równych energii wzbudzenia atomów ze stanu podstawowego do jednego ze stanów wzbudzonych o naturalnym czasie życia 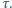 Jak długą drogę przebędzie każdy z atomów od pierwszego zderzenia z fotonem do zatrzymania? Długość fali światła laserowego wynosi
Jak długą drogę przebędzie każdy z atomów od pierwszego zderzenia z fotonem do zatrzymania? Długość fali światła laserowego wynosi 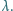 Wiązka światła jest wystarczająco intensywna. Obliczenia wykonaj dla atomów magnezu.
Wiązka światła jest wystarczająco intensywna. Obliczenia wykonaj dla atomów magnezu.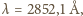
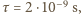
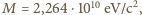
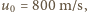
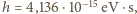
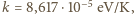
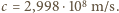
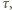 wyemituje go w losowym kierunku. W każdym akcie absorpcji foton przekazuje atomowi swój pęd
wyemituje go w losowym kierunku. W każdym akcie absorpcji foton przekazuje atomowi swój pęd 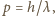 w wyniku czego atom zmniejsza swą prędkość (pęd fotonu jest przeciwnie skierowany do pędu atomu) o
w wyniku czego atom zmniejsza swą prędkość (pęd fotonu jest przeciwnie skierowany do pędu atomu) o 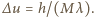 Proces powtórzy się po wyemitowaniu pochłoniętego fotonu, tj. po czasie
Proces powtórzy się po wyemitowaniu pochłoniętego fotonu, tj. po czasie 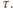 Ze względu na losowy kierunek emisji średni pęd emitowanego fotonu wynosi zero. Atomy poruszają się więc ze średnim opóźnieniem
Ze względu na losowy kierunek emisji średni pęd emitowanego fotonu wynosi zero. Atomy poruszają się więc ze średnim opóźnieniem 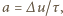 a droga przebyta do zatrzymania wynosi
a droga przebyta do zatrzymania wynosi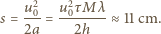
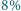 energii fali odbija się, a
energii fali odbija się, a 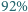 przechodzi przez płytkę. Innymi słowy, współczynnik odbicia wynosi
przechodzi przez płytkę. Innymi słowy, współczynnik odbicia wynosi 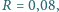 a współczynnik transmisji wynosi
a współczynnik transmisji wynosi 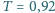 (uwzględniono już tutaj odbicie od obu powierzchni płytki). Jaki będzie współczynnik transmisji stosu złożonego z
(uwzględniono już tutaj odbicie od obu powierzchni płytki). Jaki będzie współczynnik transmisji stosu złożonego z 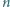 płytek?
płytek?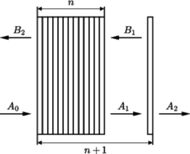
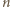 płytek wynosi
płytek wynosi 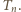 Dodając jeszcze jedną płytkę, dostajemy "złożony" stos składający się z
Dodając jeszcze jedną płytkę, dostajemy "złożony" stos składający się z 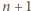 płytek. Niech na ten stos pada światło o natężeniu
płytek. Niech na ten stos pada światło o natężeniu 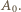 Oznaczmy natężenia światła rozchodzącego się na zewnątrz i wewnątrz "złożonego" stosu jak na rysunku.
Oznaczmy natężenia światła rozchodzącego się na zewnątrz i wewnątrz "złożonego" stosu jak na rysunku.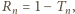 dostajemy układ równań
dostajemy układ równań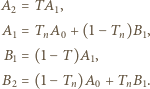
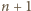 płytek, zdefiniowanej jako
płytek, zdefiniowanej jako 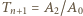 :
: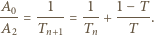
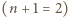 mamy
mamy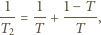
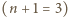 mamy
mamy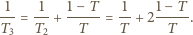
 płytek, dostajemy
płytek, dostajemy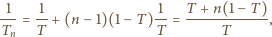
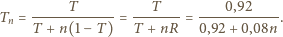
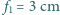 i rozpraszającej o ogniskowej
i rozpraszającej o ogniskowej 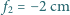 , ustawionych w odległości
, ustawionych w odległości 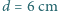 . Przedmiot znajduje się w odległości
. Przedmiot znajduje się w odległości 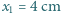 od soczewki skupiającej. Znaleźć konstrukcyjnie położenie obrazu po przejściu promieni przez układ.
od soczewki skupiającej. Znaleźć konstrukcyjnie położenie obrazu po przejściu promieni przez układ.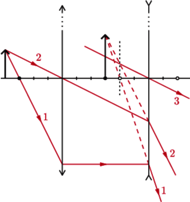
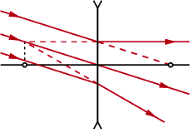
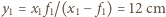 . Jest on przedmiotem pozornym dla drugiej soczewki:
. Jest on przedmiotem pozornym dla drugiej soczewki: 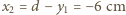 . Odległość obrazu od drugiej soczewki
. Odległość obrazu od drugiej soczewki 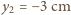 . Jest to obraz pozorny, który znajduje się między soczewkami w środku odległości między nimi.
. Jest to obraz pozorny, który znajduje się między soczewkami w środku odległości między nimi.
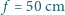 usunięto część środkową o szerokości
usunięto część środkową o szerokości 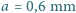 . Obie połówki soczewki stykają się. Średnica soczewki wynosi
. Obie połówki soczewki stykają się. Średnica soczewki wynosi 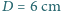 . W odległości
. W odległości 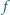 od soczewki, na jej osi optycznej, ustawiono punktowe źródło światła monochromatycznego o długości fali
od soczewki, na jej osi optycznej, ustawiono punktowe źródło światła monochromatycznego o długości fali 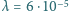 m. Z drugiej strony soczewki umieszczony jest ekran. Jakie musi być położenie ekranu, aby można było obserwować na nim prążki interferencyjne? Zakładając, że warunek ten jest spełniony, znaleźć odległość między sąsiednimi jasnymi prążkami.
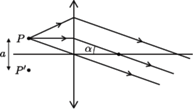
m. Z drugiej strony soczewki umieszczony jest ekran. Jakie musi być położenie ekranu, aby można było obserwować na nim prążki interferencyjne? Zakładając, że warunek ten jest spełniony, znaleźć odległość między sąsiednimi jasnymi prążkami.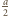 od ogniska umieścimy punkt świecący
od ogniska umieścimy punkt świecący 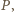 to promienie wychodzące z tego punktu po przejściu przez soczewkę utworzą wiązkę równoległą nachyloną do osi optycznej soczewki pod kątem
to promienie wychodzące z tego punktu po przejściu przez soczewkę utworzą wiązkę równoległą nachyloną do osi optycznej soczewki pod kątem 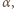 przy czym
przy czym 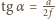 (
(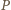 tworzą przecinające się wiązki równoległe. Z
tworzą przecinające się wiązki równoległe. Z 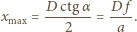
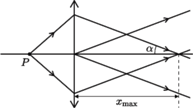
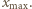 Na środku ekranu powstaje maksimum interferencyjne. Aby w p.
Na środku ekranu powstaje maksimum interferencyjne. Aby w p. 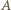 w odległości
w odległości 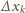 od środka ekranu powstało
od środka ekranu powstało 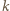 -te maksimum (
-te maksimum (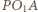 i
i 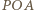 muszą się wzmacniać, zatem ich różnica dróg optycznych wynosi
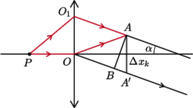
muszą się wzmacniać, zatem ich różnica dróg optycznych wynosi 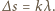 Droga optyczna promienia
Droga optyczna promienia 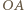 jest taka sama jak promienia
jest taka sama jak promienia 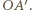 Promienie z wiązki równoległej mają w punktach
Promienie z wiązki równoległej mają w punktach 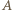 i
i 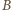 zgodne fazy, zatem
zgodne fazy, zatem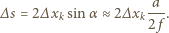
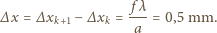
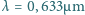 z lasera
He-Ne. Za siatką obserwuje się
z lasera
He-Ne. Za siatką obserwuje się
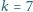 maksimów dyfrakcyjnych. Ile
wynosi stała użytej siatki dyfrakcyjnej?
maksimów dyfrakcyjnych. Ile
wynosi stała użytej siatki dyfrakcyjnej?
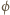 maksimów (względem prostej prostopadłej do powierzchni
siatki) są dane wzorem
maksimów (względem prostej prostopadłej do powierzchni
siatki) są dane wzorem
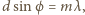 gdzie
gdzie
 jest rzędem
dyfrakcji. Ponieważ kąt dyfrakcji nie może być większy od
jest rzędem
dyfrakcji. Ponieważ kąt dyfrakcji nie może być większy od
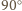 oraz
oraz
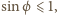 więc maksymalny rząd obserwowanego maksimum to
więc maksymalny rząd obserwowanego maksimum to
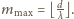 Według warunków zadania obserwuje się 7 maksimów, co
oznacza, że
Według warunków zadania obserwuje się 7 maksimów, co
oznacza, że
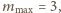 stąd stała siatki spełnia nierówność
stąd stała siatki spełnia nierówność
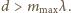 Równocześnie liczba maksimów nie może być
mniejsza niż 7, co oznacza, że
Równocześnie liczba maksimów nie może być
mniejsza niż 7, co oznacza, że
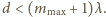 Ostatecznie
więc stała siatki musi mieścić się w granicach
Ostatecznie
więc stała siatki musi mieścić się w granicach
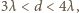 czyli
czyli
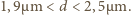
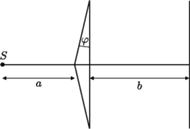
 Na ekranie powstaje obraz interferencyjny.
Znaleźć odległość pierwszego maksimum interferencyjnego od środka
ekranu. Dane są:
Na ekranie powstaje obraz interferencyjny.
Znaleźć odległość pierwszego maksimum interferencyjnego od środka
ekranu. Dane są:
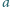 – odległość źródła od bipryzmatu,
– odległość źródła od bipryzmatu,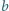 – odległość bipryzmatu od ekranu,
– odległość bipryzmatu od ekranu,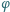 – kąt łamiący każdego z pryzmatów, który jest bardzo mały,
– kąt łamiący każdego z pryzmatów, który jest bardzo mały, – współczynnik załamania szkła, z którego wykonany jest
bipryzmat,
– współczynnik załamania szkła, z którego wykonany jest
bipryzmat,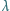 – długość fali światła emitowanego przez źródło.
– długość fali światła emitowanego przez źródło.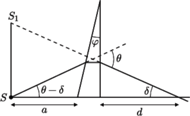
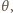 a kąt przecięcia promienia
wychodzącego z pryzmatu z osią optyczną przez
a kąt przecięcia promienia
wychodzącego z pryzmatu z osią optyczną przez
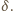 Dla małych kątów
Dla małych kątów
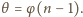 Niech punkt
Niech punkt
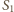 będzie przecięciem przedłużenia
promienia wychodzącego z pryzmatu z prostą prostopadłą do osi optycznej
przechodzącą przez
będzie przecięciem przedłużenia
promienia wychodzącego z pryzmatu z prostą prostopadłą do osi optycznej
przechodzącą przez
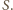 Mamy związki:
Mamy związki:
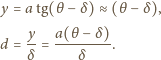
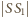 wynosi
wynosi
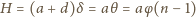
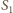 i
i
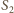 (od dolnego
pryzmatu) odległych od siebie o
(od dolnego
pryzmatu) odległych od siebie o
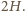 Wzór na pierwsze maksimum
interferencyjne ma postać:
Wzór na pierwsze maksimum
interferencyjne ma postać:
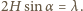 Szukana odległość między
maksimami wynosi:
Szukana odległość między
maksimami wynosi:
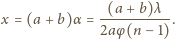

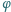 z osią pierwszego polaryzatora.
Jak zależy natężenie światła przechodzącego przez taki układ polaryzatorów
od kata
z osią pierwszego polaryzatora.
Jak zależy natężenie światła przechodzącego przez taki układ polaryzatorów
od kata
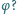 Dla jakiego kąta
Dla jakiego kąta
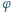 będzie ono największe, a dla jakiego
najmniejsze?
będzie ono największe, a dla jakiego
najmniejsze?
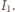 Zgodnie z prawem Malusa natężenie światła po przejściu przez
drugi polaryzator wynosi
Zgodnie z prawem Malusa natężenie światła po przejściu przez
drugi polaryzator wynosi
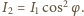 Kąt między osiami polaryzacji
drugiego i trzeciego polaryzatora wynosi
Kąt między osiami polaryzacji
drugiego i trzeciego polaryzatora wynosi
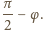 Natężenie światła za
trzecim z polaryzatorów wynosi więc
Natężenie światła za
trzecim z polaryzatorów wynosi więc
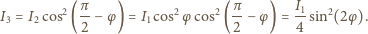
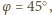 a najmniejsze
(wygaszenie) dla
a najmniejsze
(wygaszenie) dla
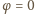 i
i
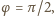 to znaczy dla dodatkowego
polaryzatora ustawionego równolegle do osi polaryzacji pierwszego albo
ostatniego z polaryzatorów.
to znaczy dla dodatkowego
polaryzatora ustawionego równolegle do osi polaryzacji pierwszego albo
ostatniego z polaryzatorów.
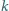 odbiciach.
odbiciach.
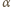 i kącie
załamania
i kącie
załamania
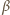 spowoduje jego odchylenie od kierunku padania o kąt
spowoduje jego odchylenie od kierunku padania o kąt
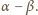 Każde odbicie wewnątrz kuli spowoduje odchylenie jego kierunku
o kat
Każde odbicie wewnątrz kuli spowoduje odchylenie jego kierunku
o kat
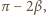 zawsze w tę samą stronę. Wreszcie przy wyjściu z kuli
promień w wyniku załamania odchyli się o kąt
zawsze w tę samą stronę. Wreszcie przy wyjściu z kuli
promień w wyniku załamania odchyli się o kąt
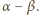 Stąd całkowita kąt
odchylenia po
Stąd całkowita kąt
odchylenia po
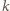 odbiciach będzie równy:
odbiciach będzie równy: