Rys. 1 Zestaw napisów przeznaczony do oglądania przez soczewkę.

Rys. 2 Sposób oglądania napisów przez soczewkę.

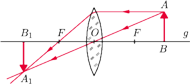
Rys. 3 Graficzne objaśnienie wytwarzania obrazu rzeczywistego przez soczewkę.

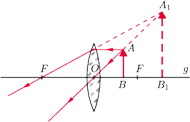
Rys. 4 Graficzne objaśnienie wytwarzania obrazu pozornego przez soczewkę.

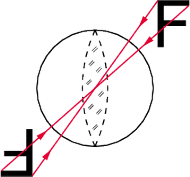
Rys. 5 Sposób odwracania obrazu przez soczewkę sferyczną.

Przed przystąpieniem do pierwszego doświadczenia butelkę, która będzie pełnić rolę soczewki, napełniamy całkowicie wodą, tak żeby nie było w niej widać żadnego pęcherzyka powietrza. Na kartce papieru piszemy (a jeszcze lepiej, drukujemy na drukarce) dwie kolumny słów, tych z rysunku 1. Najlepiej używać tzw. czcionki bezszeryfowej, czyli bez rozszerzeń na końcu odcinków i łuków tworzących litery (np. czcionka Arial). Wysokość liter powinna wynosić około 2–3 cm.

Kartkę z napisami kładziemy na dowolnej poziomej powierzchni, a tuż nad kartką trzymamy butelkę z wodą. Podłużna oś butelki powinna być też pozioma i równoległa do kierunku napisów, tak jak na rysunku 2. Patrzymy przez butelkę na wybraną linijkę napisów i staramy się zapamiętać właściwości zauważonych obrazów – ich wysokość oraz położenie w stosunku do napisów. Powoli oddalamy butelkę od kartki. Dla pewnej odległości stwierdzimy zadziwiający efekt – wysokość obrazów staje się równa wysokości napisów, a słowo z prawej strony zostaje odwrócone do góry nogami, słowo zaś z lewej strony widzimy bez odwrócenia. Zachowując osiągniętą odległość butelki do kartki, przesuwamy butelkę nad linie z innymi słowami i spostrzegamy tę samą prawidłowość. Co jest przyczyną tego zaskakującego efektu?

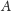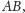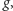Przypomnijmy sobie, jak przy użyciu optyki geometrycznej objaśniamy wytwarzanie obrazów przez soczewki. Opis taki wymaga narysowania biegu dwóch promieni świetlnych wychodzących z dowolnego punktu  przedmiotu  tak jak na rysunku 3. Jeden z promieni przechodzi równolegle do głównej osi optycznej soczewki  a drugi biegnie przez środek optyczny soczewki 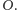 Pierwszy z tych promieni po dwukrotnym załamaniu na powierzchniach ograniczających soczewkę przechodzi przez jej ognisko 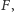 drugi zaś pokonuje soczewkę bez zmiany kierunku. W punkcie 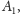 gdzie przecinają się oba promienie po przejściu przez soczewkę lub ich przedłużenia, widzimy obraz punktu 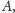 z którego te promienie wyszły. Jeżeli przecięciu uległy promienie, to obraz jest rzeczywisty i można go również zobaczyć na ustawionym w tym miejscu ekranie. Gdy przecinają się przedłużenia promieni, wówczas obraz jest pozorny (Rys. 4). Obrazu pozornego nie można zobaczyć na ekranie, a widzimy go jedynie dzięki właściwościom naszego wzroku.

Dla odległości butelki od kartki mniejszej niż ogniskowa soczewki widzieliśmy pozorne i powiększone obrazy napisów, a słowa nie były odwrócone. Oddalając soczewkę od kartki, wytworzyliśmy obrazy rzeczywiste i powiększone, przy czym powiększenie to malało w miarę oddalania butelki. A odwrócenie? Przerysowując rysunek 3 dla przypadku, w którym odległość przedmiotu od soczewki jest dwa razy większa niż jej ogniskowa, łatwo sprawdzić, że wielkość obrazu będzie taka sama, jak wielkość przedmiotu, i obraz zostanie odwrócony. Dlaczego jednak widzieliśmy odwrócony obraz słowa jedynie z prawej strony, przecież oba znajdowały się w takiej samej odległości od soczewki? Oczywiście, słowa z lewej strony miały poziomą oś symetrii, ich odwrócenie nie powodowało zatem zmiany widzianego obrazu.

A gdyby użyć soczewki sferycznej, takiej jak lupa? Soczewka sferyczna nie ma wyróżnionej osi symetrii i, wytwarzając obraz rzeczywisty, powoduje nie tylko „zamianę” górnej części obrazu na dolną, ale również prawej na lewą. Do tworzenia napisów moglibyśmy wówczas wybierać tylko litery mające środek symetrii. W alfabecie używanym w języku polskim są nimi: I, H, N, o, O, s, S, x, X. Dodatkowo można by stosować cyfry 0 i 8. Z tych znaków trudno ułożyć większą liczbę słów, zwłaszcza że kolejność znaków byłaby odwracana, np. zamiast OH widzielibyśmy HO, a zamiast 80 $ ujrzelibyśmy $ 08. Używając soczewki cylindrycznej, możemy rozszerzyć tę listę o litery z poziomą osią symetrii: B, C, c, D, E oraz K (ale trzeba odrzucić N, s, S), co daje nam już pewne możliwości słowotwórcze. Można także tworzyć symetryczne napisy, układając litery jedna nad drugą, albo, co jest trudniejsze, ale robi niewątpliwe wrażenie, spróbować odwracać napisy i rysunki, tak by powstała historyjka (zabawną realizację tego pomysłu przy użyciu innych metod przedstawia filmik http://www.youtube.com/watch?v=4mdEsouIXGM).

Zachęcam do eksperymentowania w oczekiwaniu na następny odcinek, w którym przedstawię dalsze sztuczki z użyciem soczewek.