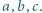Symetria w algebrze»Zadanie 1
o zadaniu...
- Zadanie pochodzi z artykułu Symetria w algebrze
- Publikacja w Delcie: luty 2019
- Publikacja elektroniczna: 1 lutego 2019
Rozwiązać układ równań w liczbach rzeczywistych.

Rozwiązać układ równań w liczbach rzeczywistych.

Rozwiązać układ równań w liczbach rzeczywistych.

Rozwiązać układ równań w liczbach rzeczywistych.

Rozwiązać układ równań w liczbach rzeczywistych.

Suma kwadratów dowolnych trzech liczb spośród 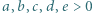 jest równa sumie sześcianów dwóch pozostałych. Wyznaczyć te liczby.
jest równa sumie sześcianów dwóch pozostałych. Wyznaczyć te liczby.
Udowodnić nierówność Schura
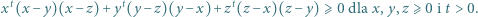
Liczby 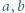 i
i  są naturalne. Iloczyn dowolnych dwóch spośród nich daje resztę
są naturalne. Iloczyn dowolnych dwóch spośród nich daje resztę 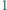 z dzielenia przez trzecią. Wyznaczyć te liczby.
z dzielenia przez trzecią. Wyznaczyć te liczby.
Wyznaczyć największą możliwą wartość wyrażenia 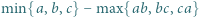 dla liczb rzeczywistych
dla liczb rzeczywistych 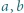 i
i 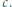
Liczby rzeczywiste 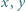 i
i  spełniają warunki:
spełniają warunki:

Dowieść, że jedna z nich jest równa sumie pozostałych
Rozwiązać równanie

w liczbach naturalnych.
Znaleźć wszystkie czwórki liczb nieujemnych 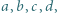 które jednocześnie spełniają nierówności
które jednocześnie spełniają nierówności
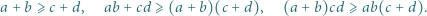
Czy istnieją takie liczby niewymierne 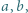 dla których liczba
dla których liczba 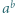 jest wymierna?
jest wymierna?
Zadanie 766 zaproponował pan Piotr Kumor z Olsztyna.
Znaleźć liczbę rzeczywistą 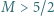 taką, że dla dowolnych liczb dodatnich
taką, że dla dowolnych liczb dodatnich 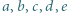 zachodzi nierówność
zachodzi nierówność
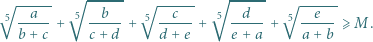 |
Im większa liczba 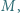 tym lepsze rozwiązanie.
tym lepsze rozwiązanie.
Dany jest wielomian 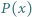 stopnia 2, o współczynnikach rzeczywistych, oraz liczba naturalna
stopnia 2, o współczynnikach rzeczywistych, oraz liczba naturalna 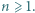 Udowodnić, że może istnieć co najwyżej jeden wielomian
Udowodnić, że może istnieć co najwyżej jeden wielomian 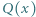 stopnia
stopnia 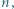 spełniający równanie
spełniający równanie 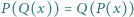 dla
dla 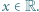
Nieujemne liczby rzeczywiste 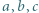 spełniają nierówność
spełniają nierówność 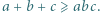 Udowodnić, że
Udowodnić, że 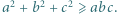
Zadanie 760 zaproponował pan Paweł Kubit z Krakowa.
Dowieść, że istnieje nieskończenie wiele dodatnich liczb rzeczywistych 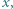 dla których każda z liczb
dla których każda z liczb 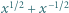 oraz
oraz 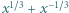 jest całkowita.
jest całkowita.
Niech 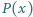 będzie takim wielomianem o współczynnikach rzeczywistych, że
będzie takim wielomianem o współczynnikach rzeczywistych, że
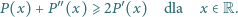
Dowieść, że 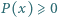 dla
dla 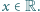
Zadanie 754 zaproponował pan Mikołaj Pater.
Znaleźć wszystkie trójki liczb rzeczywistych 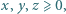 spełniające układ równań
spełniające układ równań
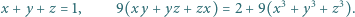
Dodatnie liczby rzeczywiste 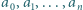 są takie, że
są takie, że 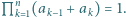 Udowodnić, że
Udowodnić, że
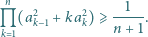
Liczby rzeczywiste 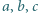 są takie, że
są takie, że 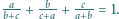 Sprawdzić, że wartość wyrażenia
Sprawdzić, że wartość wyrażenia
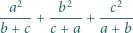
nie zależy od wartości