Podstawmy, kolejno, 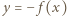 oraz
oraz 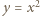 ; otrzymujemy równania
; otrzymujemy równania
oraz
które po dodaniu stronami i redukcji dają związek 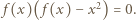 Zatem dla każdej liczby
Zatem dla każdej liczby  ma miejsce alternatywa:
ma miejsce alternatywa: 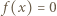 lub
lub 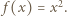 Stąd, w szczególności,
Stąd, w szczególności, 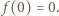
Jeśli 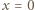 jest jedynym miejscem zerowym funkcji
jest jedynym miejscem zerowym funkcji 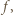 to
to 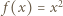 dla wszystkich
dla wszystkich  Łatwo sprawdzić, że ta funkcja spełnia zadane równanie. Pozostaje przypadek, gdy
Łatwo sprawdzić, że ta funkcja spełnia zadane równanie. Pozostaje przypadek, gdy 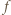 ma jeszcze jakieś miejsce zerowe
ma jeszcze jakieś miejsce zerowe 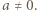 Wykażemy, że wówczas
Wykażemy, że wówczas 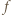 jest tożsamościowo równa zeru.
jest tożsamościowo równa zeru.
Przypuśćmy, że 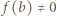 dla pewnego
dla pewnego 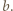 Biorąc w zadanym równaniu
Biorąc w zadanym równaniu 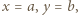 dostajemy
dostajemy 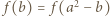 ; ta liczba nie jest zerem, więc z wcześniejszej alternatywy wynika, że wynosi ona jednocześnie
; ta liczba nie jest zerem, więc z wcześniejszej alternatywy wynika, że wynosi ona jednocześnie 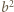 oraz
oraz 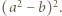 Przyrównanie tych wartości daje równość
Przyrównanie tych wartości daje równość 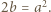 To liczba dodatnia; stąd
To liczba dodatnia; stąd 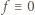 w przedziale
w przedziale ![|(−∞ ,0].](/math/temat/matematyka/analiza/zadania/2019/10/31/zm-k44-789/9x-86016eea9da0a9d7e7b58d20a6007ab7e898b219-im-66,57,43-FF,FF,FF.gif) Weźmy teraz dowolną liczbę
Weźmy teraz dowolną liczbę 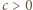 i w wyjściowym równaniu podstawmy
i w wyjściowym równaniu podstawmy 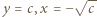 (już wiemy, że
(już wiemy, że 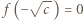 ). Wychodzi
). Wychodzi 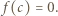 Tak więc
Tak więc 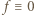 także w przedziale
także w przedziale 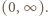
Wniosek (odpowiedź): jedynymi funkcjami spełniającymi podane równanie są: 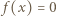 (dla wszystkich
(dla wszystkich 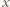 ) oraz
) oraz  (dla wszystkich
(dla wszystkich  ).
).
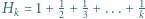 dla całkowitych dodatnich
dla całkowitych dodatnich 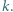 Udowodnić, że
Udowodnić, że 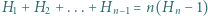 dla naturalnych
dla naturalnych 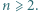
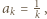 gdzie
gdzie 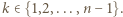
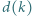 oznacza liczbę dzielników liczby naturalnej
oznacza liczbę dzielników liczby naturalnej 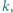 zaś
zaś 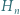 - jak w poprzednim zadaniu. Dowieść, że
- jak w poprzednim zadaniu. Dowieść, że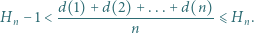
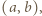 dla których
dla których 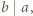 gdzie
gdzie 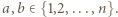 Po sporządzeniu tabeli w kolumnach mamy kolejno
Po sporządzeniu tabeli w kolumnach mamy kolejno 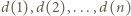 par, a w wierszach
par, a w wierszach 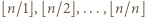 par. Trzeba jeszcze zastosować nierówność
par. Trzeba jeszcze zastosować nierówność 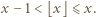
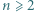 zachodzi równość
zachodzi równość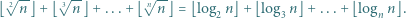
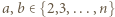 zaznaczamy takie pola
zaznaczamy takie pola 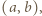 dla których
dla których 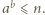 Wówczas w
Wówczas w 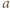 -tej kolumnie mamy
-tej kolumnie mamy 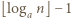 zaznaczonych pól, zaś w
zaznaczonych pól, zaś w 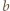 -tym wierszu jest ich
-tym wierszu jest ich 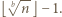
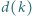 będzie jak w zadaniu 6. Ustalmy liczbę rzeczywistą
będzie jak w zadaniu 6. Ustalmy liczbę rzeczywistą 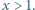 Dowieść, że dla wszystkich naturalnych
Dowieść, że dla wszystkich naturalnych 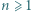 zachodzi nierówność
zachodzi nierówność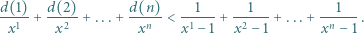
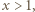 mamy
mamy 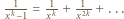 Dla
Dla 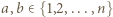 w polu
w polu 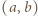 tabeli umieszczamy liczbę
tabeli umieszczamy liczbę 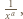 jeśli
jeśli 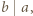 w przeciwnym razie umieszczamy 0. Sumując kolumnami, otrzymamy lewą stronę dowodzonej nierówności, natomiast wierszami - liczbę mniejszą od prawej strony.
w przeciwnym razie umieszczamy 0. Sumując kolumnami, otrzymamy lewą stronę dowodzonej nierówności, natomiast wierszami - liczbę mniejszą od prawej strony.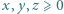 przyjmijmy:
przyjmijmy: 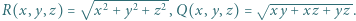 Wyznaczyć najmniejszą możliwą wartość wyrażenia
Wyznaczyć najmniejszą możliwą wartość wyrażenia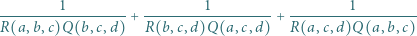
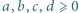 spełniających warunek
spełniających warunek 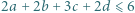 oraz wyznaczyć wszystkie czwórki
oraz wyznaczyć wszystkie czwórki 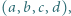 dla których to minimum jest osiągane.
dla których to minimum jest osiągane. (stale zakładamy, że wszystkie mianowniki są dodatnie). Dwukrotnie stosujemy nierówność między średnimi (po drodze przegrupowując czynniki):
(stale zakładamy, że wszystkie mianowniki są dodatnie). Dwukrotnie stosujemy nierówność między średnimi (po drodze przegrupowując czynniki):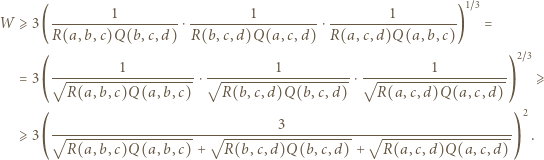
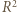 i
i 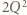 ), dostajemy oszacowanie
), dostajemy oszacowanie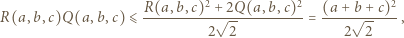
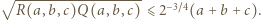 Stąd i z analogicznego oszacowania dla trójek
Stąd i z analogicznego oszacowania dla trójek 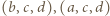 uzyskujemy kontynuację wcześniejszego ciągu nierówności:
uzyskujemy kontynuację wcześniejszego ciągu nierówności: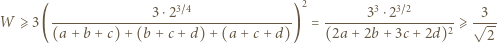
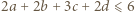 z założenia). Znaleziona wartość zostaje osiągnięta, gdy wszystkie nierówności stają się równościami; więc gdy
z założenia). Znaleziona wartość zostaje osiągnięta, gdy wszystkie nierówności stają się równościami; więc gdy 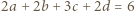 oraz
oraz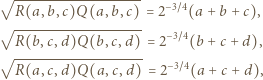
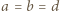 oraz
oraz 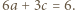 Ponadto - oznaczając krótko
Ponadto - oznaczając krótko 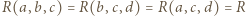 (i podobnie
(i podobnie 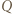 ) - musimy mieć równość
) - musimy mieć równość 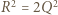 (do takiej pary też była stosowana nierówność między średnimi) - czyli
(do takiej pary też była stosowana nierówność między średnimi) - czyli 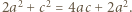 Wraz z równością
Wraz z równością 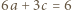 daje to alternatywę:
daje to alternatywę: 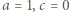 lub
lub 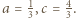 Dla czwórek
Dla czwórek 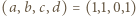 oraz
oraz 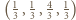 wyznaczone oszacowanie
wyznaczone oszacowanie 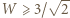 przechodzi w równość. Zatem szukane minimum wynosi
przechodzi w równość. Zatem szukane minimum wynosi 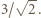
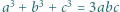 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 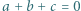 lub
lub 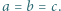
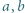 spełniają równość
spełniają równość 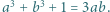 Wyznaczyć wszystkie możliwe wartości wyrażenia
Wyznaczyć wszystkie możliwe wartości wyrażenia 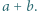
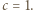 Są tu dwa przypadki do rozważania.
Są tu dwa przypadki do rozważania.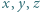 są rzeczywiste. Udowodnić, że jeśli
są rzeczywiste. Udowodnić, że jeśli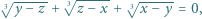
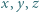 są równe.
są równe.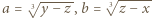 i
i 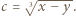
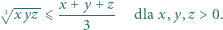
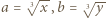 i
i 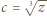 w tożsamości.
w tożsamości.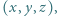 które spełniają równości
które spełniają równości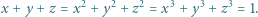
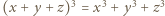 i dzięki tożsamości (1) z artykułu dochodzimy do wniosku, że wśród liczb
i dzięki tożsamości (1) z artykułu dochodzimy do wniosku, że wśród liczb  występuje co najmniej jedna para liczb przeciwnych.
występuje co najmniej jedna para liczb przeciwnych. Uczynić to bez pomocy kalkulatora, wykonując przy tym możliwie najmniej rachunków.
Uczynić to bez pomocy kalkulatora, wykonując przy tym możliwie najmniej rachunków.
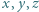 spełniają równość
spełniają równość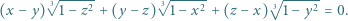
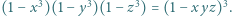
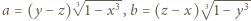 i
i 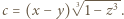 Następnie zauważyć, że
Następnie zauważyć, że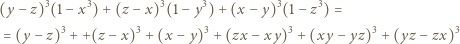
 spełniające równanie
spełniające równanie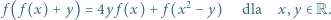
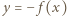 oraz
oraz 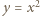 ; otrzymujemy równania
; otrzymujemy równania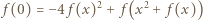
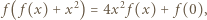
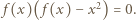 Zatem dla każdej liczby
Zatem dla każdej liczby 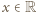 ma miejsce alternatywa:
ma miejsce alternatywa: 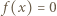 lub
lub 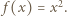 Stąd, w szczególności,
Stąd, w szczególności, 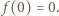
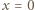 jest jedynym miejscem zerowym funkcji
jest jedynym miejscem zerowym funkcji 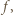 to
to 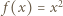 dla wszystkich
dla wszystkich  Łatwo sprawdzić, że ta funkcja spełnia zadane równanie. Pozostaje przypadek, gdy
Łatwo sprawdzić, że ta funkcja spełnia zadane równanie. Pozostaje przypadek, gdy 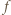 ma jeszcze jakieś miejsce zerowe
ma jeszcze jakieś miejsce zerowe 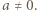 Wykażemy, że wówczas
Wykażemy, że wówczas 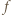 jest tożsamościowo równa zeru.
jest tożsamościowo równa zeru.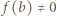 dla pewnego
dla pewnego 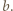 Biorąc w zadanym równaniu
Biorąc w zadanym równaniu 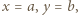 dostajemy
dostajemy 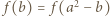 ; ta liczba nie jest zerem, więc z wcześniejszej alternatywy wynika, że wynosi ona jednocześnie
; ta liczba nie jest zerem, więc z wcześniejszej alternatywy wynika, że wynosi ona jednocześnie 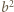 oraz
oraz 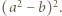 Przyrównanie tych wartości daje równość
Przyrównanie tych wartości daje równość 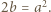 To liczba dodatnia; stąd
To liczba dodatnia; stąd 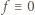 w przedziale
w przedziale ![|(−∞ ,0].](/math/temat/matematyka/analiza/zadania/2019/10/31/zm-k44-789/9x-86016eea9da0a9d7e7b58d20a6007ab7e898b219-im-66,57,43-FF,FF,FF.gif) Weźmy teraz dowolną liczbę
Weźmy teraz dowolną liczbę 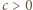 i w wyjściowym równaniu podstawmy
i w wyjściowym równaniu podstawmy 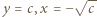 (już wiemy, że
(już wiemy, że 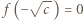 ). Wychodzi
). Wychodzi 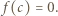 Tak więc
Tak więc 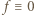 także w przedziale
także w przedziale 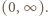
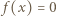 (dla wszystkich
(dla wszystkich 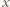 ) oraz
) oraz  (dla wszystkich
(dla wszystkich  ).
).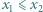 i
i 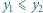 spełniają równości
spełniają równości 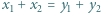 oraz
oraz 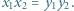 Udowodnić, że
Udowodnić, że 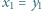 i
i 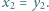
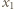 i
i 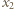 są, na mocy wzorów Viete'a, pierwiastkami tego samego trójmianu kwadratowego, co liczby
są, na mocy wzorów Viete'a, pierwiastkami tego samego trójmianu kwadratowego, co liczby 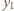 oraz
oraz 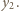
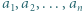 będą ustalonymi liczbami rzeczywistymi. Dla jakiego
będą ustalonymi liczbami rzeczywistymi. Dla jakiego 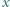 wartość funkcji
wartość funkcji
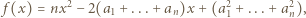
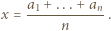
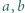 i
i  spełniają nierówność
spełniają nierówność 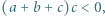 przy czym
przy czym 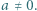 Wykazać, że
Wykazać, że 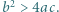
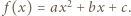 Wówczas mamy
Wówczas mamy 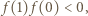 więc funkcja
więc funkcja 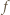 przyjmuje zarówno dodatnie i ujemne wartości, skąd
przyjmuje zarówno dodatnie i ujemne wartości, skąd 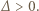
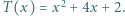
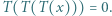
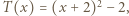
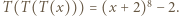
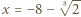
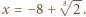
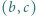
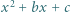
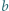
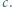
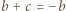
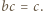
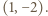


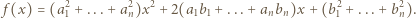
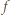 przyjmuje wyłącznie wartości nieujemne, więc
przyjmuje wyłącznie wartości nieujemne, więc 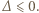 Jest to nierówność równoważna dowodzonej.
Jest to nierówność równoważna dowodzonej.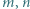 oraz
oraz 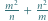 są całkowite. Udowodnić, że liczba
są całkowite. Udowodnić, że liczba 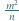 również jest całkowita.
również jest całkowita.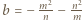 oraz
oraz 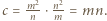 Liczby
Liczby 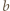 i
i  są całkowite, zaś liczby wymierne
są całkowite, zaś liczby wymierne 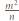 i
i 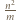 są pierwiastkami trójmianu (unormowanego)
są pierwiastkami trójmianu (unormowanego) 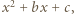 więc są całkowite.
więc są całkowite.