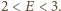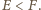Klub 44M - zadania XI 2013»Zadanie 670
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania XI 2013
- Publikacja w Delcie: listopad 2013
- Publikacja elektroniczna: 1 listopada 2013
- Artykuł źródłowy w wersji do druku [application/pdf]: (114 KB)
Zadanie 670 zaproponował pan Paweł Kubit z Krakowa.
Udowodnić nierówność
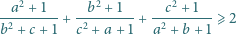
dla liczb rzeczywistych
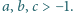
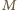 będzie średnią arytmetyczną liczb
będzie średnią arytmetyczną liczb
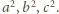 Oznaczmy:
Oznaczmy:
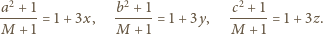
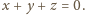 Stąd
Stąd
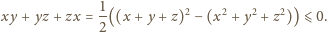
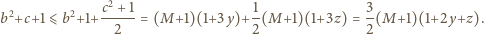
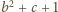 jest dodatnia (tu korzystamy z założenia, że
jest dodatnia (tu korzystamy z założenia, że
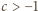 ), zatem po prawej stronie ostatniej nierówności mamy również
liczbę dodatnią, i wobec tego
), zatem po prawej stronie ostatniej nierówności mamy również
liczbę dodatnią, i wobec tego
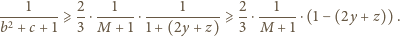
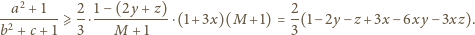
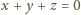 oraz
oraz
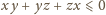 ):
):
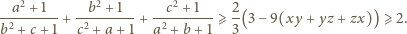
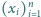 liczb rzeczywistych
dodatnich prawdziwa jest nierówność
liczb rzeczywistych
dodatnich prawdziwa jest nierówność
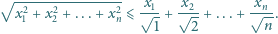
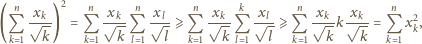
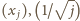 są malejące.
są malejące.
 i liczby całkowitej
i liczby całkowitej
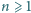 prawdziwa jest nierówność
prawdziwa jest nierówność
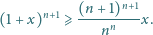
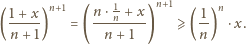
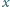 spełnia równanie
spełnia równanie
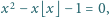 to każda potęga liczby
to każda potęga liczby
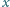 o wykładniku
dodatnim nieparzystym także spełnia to równanie.
o wykładniku
dodatnim nieparzystym także spełnia to równanie.
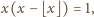 to
to
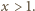 Wykażemy indukcyjnie, że dla
każdej liczby nieparzystej
Wykażemy indukcyjnie, że dla
każdej liczby nieparzystej
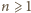 różnica
różnica
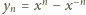 jest liczbą
całkowitą.
jest liczbą
całkowitą.
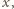 widzimy, że
widzimy, że
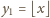 (liczba całkowita). Zatem także liczba
(liczba całkowita). Zatem także liczba
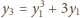 jest całkowita.
jest całkowita.
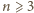 i załóżmy, że liczby
i załóżmy, że liczby
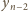 oraz
oraz
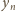 są całkowite. Przekształcenie
są całkowite. Przekształcenie
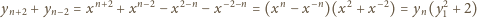
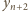 też jest całkowita. Przez indukcję
wnosimy, że liczby
też jest całkowita. Przez indukcję
wnosimy, że liczby
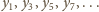 wszystkie są całkowite.
wszystkie są całkowite.
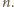 Ze związków
Ze związków
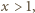
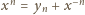 (
(
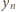 całkowite) wynika, że
całkowite) wynika, że
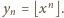 Zachodzi
więc równość
Zachodzi
więc równość
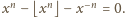 Wystarczy ją pomnożyć przez
Wystarczy ją pomnożyć przez
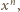 by uzyskać tezę zadania.
by uzyskać tezę zadania.
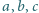 jest spełniona
nierówność
jest spełniona
nierówność
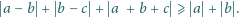
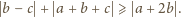
 i wystarczy teraz udowodnić,
że
i wystarczy teraz udowodnić,
że
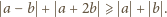
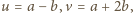 tzn.
tzn.
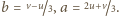 Otrzymujemy wówczas
Otrzymujemy wówczas
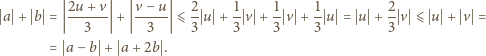

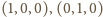 i
i
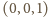 oraz sferę o środku w punkcie
oraz sferę o środku w punkcie
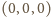 i promieniu 1. Sfera ta przechodzi przez te same trzy punkty, więc
przecina się z daną płaszczyzną wzdłuż okręgu przez nie wyznaczonego. Stąd
układ równań ma nieskończenie wiele rozwiązań.
i promieniu 1. Sfera ta przechodzi przez te same trzy punkty, więc
przecina się z daną płaszczyzną wzdłuż okręgu przez nie wyznaczonego. Stąd
układ równań ma nieskończenie wiele rozwiązań.

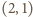 i promieniu
i promieniu
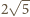 oraz
okrąg o środku
oraz
okrąg o środku
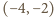 i promieniu
i promieniu
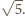 Odległość między
środkami tych okręgów równa jest
Odległość między
środkami tych okręgów równa jest
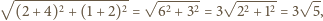
 jest nie mniejsza od
jest nie mniejsza od
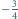 oraz
oraz
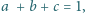 to
to

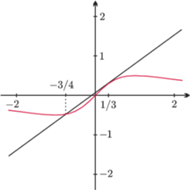
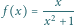
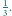
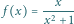
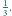
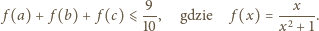
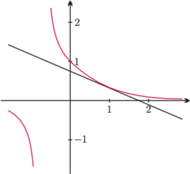
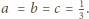 Równanie
stycznej do funkcji
Równanie
stycznej do funkcji
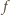 w punkcie
w punkcie
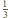 ma postać
ma postać
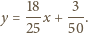
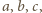 spełniających warunek
spełniających warunek
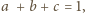 suma wartości wyrażenia
suma wartości wyrażenia
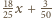 jest równa
jest równa
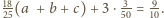
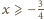 prawdziwa jest
nierówność
prawdziwa jest
nierówność
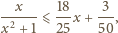
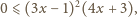
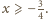
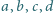 zachodzi
nierówność
zachodzi
nierówność

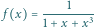
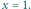
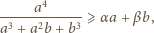
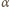 i
i
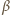 są pewnymi liczbami rzeczywistymi. Dzieląc obie
strony przez
są pewnymi liczbami rzeczywistymi. Dzieląc obie
strony przez
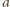 i podstawiając
i podstawiając
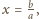 otrzymujemy
otrzymujemy
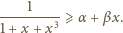
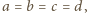 więc musimy tak dobrać współczynniki
więc musimy tak dobrać współczynniki
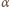 i
i
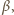 aby równość zachodziła dla
aby równość zachodziła dla
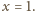 Znajdując
równanie stycznej do wykresu funkcji
Znajdując
równanie stycznej do wykresu funkcji
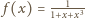 w punkcie
w punkcie
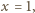 otrzymujemy współczynniki
otrzymujemy współczynniki
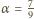 i
i
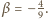
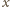 zachodzi
nierówność
zachodzi
nierówność
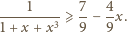
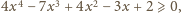 a następnie
doprowadzamy nierówność do postaci
a następnie
doprowadzamy nierówność do postaci
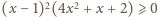 – teraz
widać, że to prawda dla dowolnego
– teraz
widać, że to prawda dla dowolnego
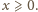
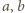 zachodzi nierówność
zachodzi nierówność
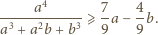
 zachodzi
nierówność
zachodzi
nierówność

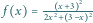
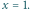
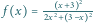
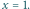
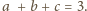 (Jest to bardziej wygodne niż założenie
(Jest to bardziej wygodne niż założenie
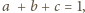 gdyż
równość zachodzi dla
gdyż
równość zachodzi dla
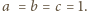 ) Wówczas dana nierówność
przyjmuje postać
) Wówczas dana nierówność
przyjmuje postać
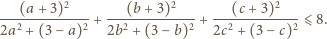
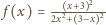 w punkcie
w punkcie
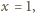 otrzymujemy do udowodnienia nierówność
otrzymujemy do udowodnienia nierówność
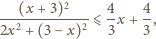
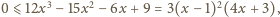 co
jest prawdą dla
co
jest prawdą dla
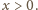
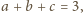 nierówność
zachodzi nie tylko dla liczb dodatnich, ale także dla nie mniejszych niż
nierówność
zachodzi nie tylko dla liczb dodatnich, ale także dla nie mniejszych niż
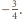
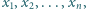 gdzie
gdzie
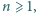 spełniają warunki
spełniają warunki

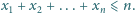
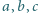 zachodzi
nierówność
zachodzi
nierówność

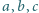 zachodzi
nierówność
zachodzi
nierówność

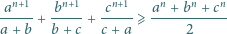
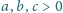 oraz liczb całkowitych
oraz liczb całkowitych
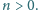
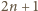 liczb, mianowicie
liczb, mianowicie
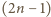 -krotnie powtórzonej liczby
-krotnie powtórzonej liczby
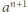 oraz liczb
oraz liczb
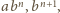 jest nie mniejsza od ich średniej geometrycznej, równej
jest nie mniejsza od ich średniej geometrycznej, równej
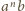 :
:
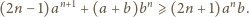
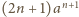 i po prostym przekształceniu
otrzymujemy
i po prostym przekształceniu
otrzymujemy
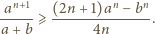
 oraz
oraz
 po czym dodać te trzy nierówności, by uzyskać tezę
zadania.
po czym dodać te trzy nierówności, by uzyskać tezę
zadania.
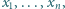 które są nie mniejsze niż
które są nie mniejsze niż
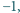 spełniają
równość
spełniają
równość
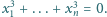 Udowodnić, że
Udowodnić, że
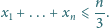
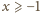 zachodzi
zachodzi
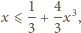
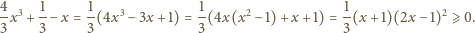
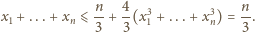
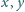 spełniają równość
spełniają równość
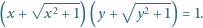
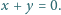
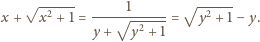
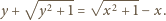
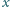 istnieją takie liczby niewymierne
istnieją takie liczby niewymierne
 i
i
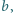 że
że
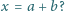
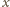 można wskazać odpowiednie liczby
można wskazać odpowiednie liczby
 i
i
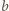 w następujący sposób.
w następujący sposób.
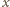 jest niewymierna, to niewymierne są także liczby
jest niewymierna, to niewymierne są także liczby
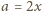 oraz
oraz
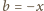 (dlaczego?). Wówczas, oczywiście,
(dlaczego?). Wówczas, oczywiście,
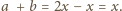
 jest wymierna, to liczba
jest wymierna, to liczba
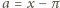 jest
niewymierna (dlaczego?). Wówczas, przyjmując
jest
niewymierna (dlaczego?). Wówczas, przyjmując
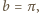 mamy
mamy
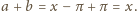

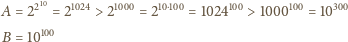
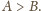
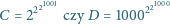
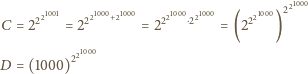
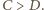

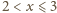 mamy
mamy
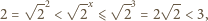
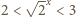 i dalej
i dalej
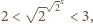 skąd dochodzimy do
skąd dochodzimy do