Oznaczmy sumę daną w zadaniu przez 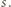 Udowodnimy najpierw, że liczba
Udowodnimy najpierw, że liczba  nie jest całkowita. Zauważmy w tym celu, że dla dowolnej liczby całkowitej
nie jest całkowita. Zauważmy w tym celu, że dla dowolnej liczby całkowitej 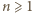 zachodzą nierówności
zachodzą nierówności

Pierwsza z nich jest oczywista, zaś druga po podniesieniu do kwadratu redukuje się do

co jest prawdą, gdyż 
W szczególności dla dowolnego 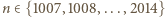 prawdziwe są nierówności
prawdziwe są nierówności

Wynika stąd, że suma  nie jest liczbą całkowitą, gdyż część ułamkowa każdego z jej
nie jest liczbą całkowitą, gdyż część ułamkowa każdego z jej 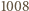 składników jest mniejsza niż
składników jest mniejsza niż 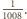 Dowodzi to naszego stwierdzenia.
Dowodzi to naszego stwierdzenia.
Może się wydawać, że do osiągnięcia celu jest jeszcze daleko. Liczba, która nie jest całkowita, nie musi przecież od razu być niewymierna. W tym jednak momencie można zacząć podejrzewać, jaką rolę odegrają własności wielomianów. W następnym kroku udowodnimy bowiem, że istnieje wielomian unormowany 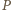 o współczynnikach całkowitych, taki, że
o współczynnikach całkowitych, taki, że 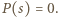 Stąd już natychmiast otrzymamy tezę zadania, gdyż z twierdzenia o pierwiastku wymiernym wynika, że każdy wymierny pierwiastek wielomianu
Stąd już natychmiast otrzymamy tezę zadania, gdyż z twierdzenia o pierwiastku wymiernym wynika, że każdy wymierny pierwiastek wielomianu 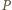 jest również całkowity. W szczególności, skoro
jest również całkowity. W szczególności, skoro 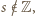 to tym samym
to tym samym 
Za pomocą indukcji po  wykażemy ogólniejsze stwierdzenie: dla dowolnych liczb całkowitych
wykażemy ogólniejsze stwierdzenie: dla dowolnych liczb całkowitych 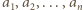 istnieje unormowany wielomian
istnieje unormowany wielomian 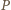 o współczynnikach całkowitych, dla którego
o współczynnikach całkowitych, dla którego

Gdy 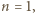 wystarczy przyjąć
wystarczy przyjąć 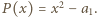 Załóżmy więc, że
Załóżmy więc, że 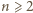 oraz istnieje wielomian unormowany
oraz istnieje wielomian unormowany 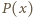 o współczynnikach całkowitych, dla którego
o współczynnikach całkowitych, dla którego 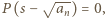 gdzie
gdzie 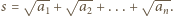 Przyjmijmy, że stopień wielomianu
Przyjmijmy, że stopień wielomianu 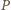 to
to  i że
i że 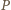 zapisuje się w postaci
zapisuje się w postaci 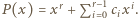 W szczególności
W szczególności

Po rozwinięciu wszystkich potęg ze wzoru dwumianowego Newtona otrzymujemy równanie postaci

gdzie 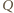 i
i 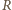 są wielomianami o współczynnikach całkowitych stopnia mniejszego niż
są wielomianami o współczynnikach całkowitych stopnia mniejszego niż 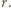 Przenosząc składnik
Przenosząc składnik 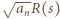 na drugą stronę i podnosząc obie strony równości do kwadratu, dostajemy
na drugą stronę i podnosząc obie strony równości do kwadratu, dostajemy

W szczególności liczba  jest pierwiastkiem unormowanego wielomianu
jest pierwiastkiem unormowanego wielomianu

Kończy to zarówno dowód indukcyjny, jak i rozwiązanie zadania.
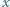 oraz dla każdej dodatniej liczby całkowitej
oraz dla każdej dodatniej liczby całkowitej 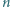 istnieje co najmniej
istnieje co najmniej 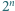 różnych wyborów znaków
różnych wyborów znaków 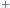 i
i  w wyrażeniu
w wyrażeniu 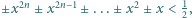 dla których ta nierówność jest spełniona.
dla których ta nierówność jest spełniona.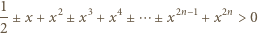
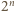 możliwych wyborów znaków. Rzeczywiście, lewą stronę powyższej nierówności można zapisać w postaci
możliwych wyborów znaków. Rzeczywiście, lewą stronę powyższej nierówności można zapisać w postaci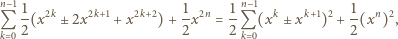
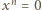 oraz
oraz 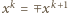 (dla
(dla 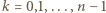 i pewnych wyborów znaków
i pewnych wyborów znaków 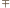 ) nie mogą wszystkie zachodzić jednocześnie.
) nie mogą wszystkie zachodzić jednocześnie.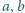 spełniają warunek
spełniają warunek 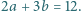 Wykazać, że dla każdej liczby naturalnej
Wykazać, że dla każdej liczby naturalnej 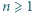 zachodzi nierówność
zachodzi nierówność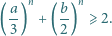
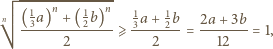
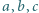 większe od
większe od 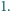 Następnie na kartce zapisano w przypadkowej kolejności cztery liczby, będące wynikami działań
Następnie na kartce zapisano w przypadkowej kolejności cztery liczby, będące wynikami działań 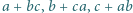 oraz
oraz 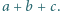 Czy znając liczby napisane na kartce można jednoznacznie określić, jakie trzy liczby znajdują się na tablicy?
Czy znając liczby napisane na kartce można jednoznacznie określić, jakie trzy liczby znajdują się na tablicy?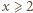 oraz
oraz 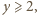 to
to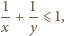
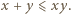 To oznacza, że
To oznacza, że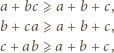
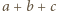 ; oznaczmy tę liczbę przez
; oznaczmy tę liczbę przez 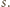 Pozostałe liczby oznaczmy przez
Pozostałe liczby oznaczmy przez 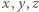 i przyjmijmy (bez straty ogólności, z uwagi na symetrię ról liczb z tablicy), że
i przyjmijmy (bez straty ogólności, z uwagi na symetrię ról liczb z tablicy), że 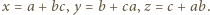 Wówczas
Wówczas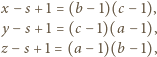
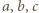 są większe od
są większe od 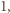 to
to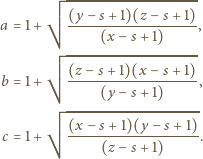
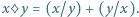 Niech
Niech 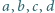 będą liczbami, spełniającymi równanie
będą liczbami, spełniającymi równanie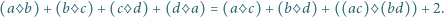
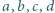 mogą być czterema różnymi liczbami? Czy mogą być wśród nich trzy różne liczby?
mogą być czterema różnymi liczbami? Czy mogą być wśród nich trzy różne liczby?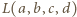 oznacza lewą stronę podanego równania, pomnożoną przez
oznacza lewą stronę podanego równania, pomnożoną przez 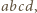 i niech
i niech 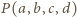 oznacza prawą stronę tego równania, pomnożoną przez
oznacza prawą stronę tego równania, pomnożoną przez 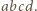 Są to wielomiany czterech zmiennych, jednorodne, czwartego stopnia. Skontrolujmy ich wartości, gdy np.
Są to wielomiany czterech zmiennych, jednorodne, czwartego stopnia. Skontrolujmy ich wartości, gdy np. 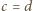 :
: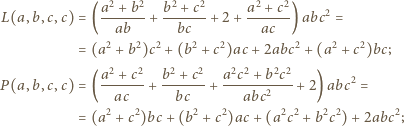
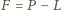 dzieli się przez dwumian
dzieli się przez dwumian 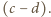 Analogicznie (wobec niezmienniczości przy cyklicznym przesunięciu zmiennych) dzieli się przez dwumiany
Analogicznie (wobec niezmienniczości przy cyklicznym przesunięciu zmiennych) dzieli się przez dwumiany 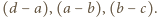 Stąd wniosek, że dzieli się przez iloczyn tych dwumianów, a iloraz jest pewną stałą. Biorąc dowolne różne liczby
Stąd wniosek, że dzieli się przez iloczyn tych dwumianów, a iloraz jest pewną stałą. Biorąc dowolne różne liczby 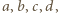 stwierdzamy, że ta stała to 1. Tak więc
stwierdzamy, że ta stała to 1. Tak więc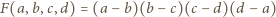
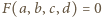 nie jest spełnione dla żadnej czwórki różnych liczb
nie jest spełnione dla żadnej czwórki różnych liczb 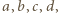 jest zaś spełnione dla wielu czwórek utworzonych z trzech różnych liczb (z jednym powtórzeniem).
jest zaś spełnione dla wielu czwórek utworzonych z trzech różnych liczb (z jednym powtórzeniem).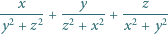
 mogą być dowolnymi liczbami dodatnimi, spełniającymi warunek
mogą być dowolnymi liczbami dodatnimi, spełniającymi warunek 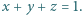
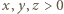 o sumie równej 1. Funkcja
o sumie równej 1. Funkcja 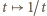 jest wypukła w przedziale
jest wypukła w przedziale 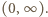 Stosujemy do niej nierówność Jensena dla trójki punktów
Stosujemy do niej nierówność Jensena dla trójki punktów 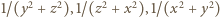 z wagami
z wagami 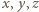 :
: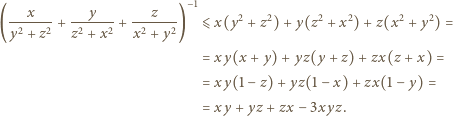
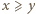 oraz
oraz 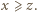 Wówczas
Wówczas 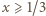 oraz
oraz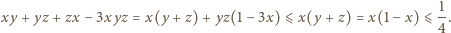
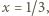 zaś druga - tylko dla
zaś druga - tylko dla 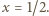 Stąd wniosek, że
Stąd wniosek, że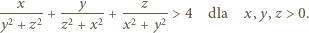
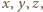 wśród których jedna jest zerem, rozważana suma nadal miałaby sens oraz przyjęłaby wartość 4 dla
wśród których jedna jest zerem, rozważana suma nadal miałaby sens oraz przyjęłaby wartość 4 dla 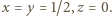 Przy założeniu, że
Przy założeniu, że 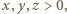 wartość 4 jest (jak widać) nieosiągalna; ale jest granicą badanej sumy np. dla
wartość 4 jest (jak widać) nieosiągalna; ale jest granicą badanej sumy np. dla 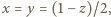 gdy
gdy 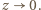 Jest więc jej kresem dolnym.
Jest więc jej kresem dolnym.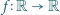 o następujących własnościach:
o następujących własnościach: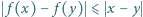 dla
dla 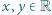 ;
;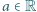 ciąg
ciąg 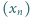 określony wzorami
określony wzorami 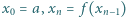 (dla
(dla 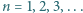 ) jest ciągiem arytmetycznym.
) jest ciągiem arytmetycznym.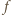 będzie funkcją, spełniającą postawione warunki, i przyjmijmy, że funkcja
będzie funkcją, spełniającą postawione warunki, i przyjmijmy, że funkcja 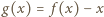 nie jest stała. Istnieją więc liczby
nie jest stała. Istnieją więc liczby 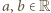 dla których
dla których 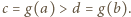 W drugim z warunków, podanych w zadaniu, przyjmujemy
W drugim z warunków, podanych w zadaniu, przyjmujemy 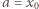 i tworzymy ciąg arytmetyczny
i tworzymy ciąg arytmetyczny 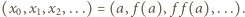 Skoro
Skoro 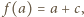 zatem
zatem 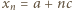 (dla wszystkich
(dla wszystkich  ). Jednocześnie
). Jednocześnie 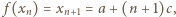 czyli
czyli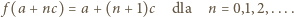
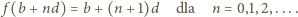
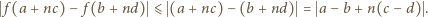
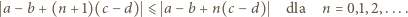
 wyrażenia ujęte w symbol wartości bezwzględnej mają wartość dodatnią (bo
wyrażenia ujęte w symbol wartości bezwzględnej mają wartość dodatnią (bo 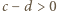 ). Można więc opuścić moduły. Ale zależność (3) - po skasowaniu modułów - redukuje się do postaci
). Można więc opuścić moduły. Ale zależność (3) - po skasowaniu modułów - redukuje się do postaci 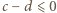 ; sprzeczność.
; sprzeczność.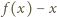 musi być stała. Jasne, że każda funkcja postaci
musi być stała. Jasne, że każda funkcja postaci 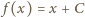 spełnia wymagane warunki.
spełnia wymagane warunki.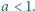 Obliczyć kres górny zbioru wartości wyrażenia
Obliczyć kres górny zbioru wartości wyrażenia 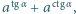 gdy zmienna
gdy zmienna 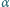 przebiega przedział
przebiega przedział 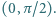
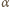 przebiega przedział
przebiega przedział 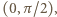 wartość
wartość 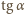 przebiega zbiór wszystkich liczb dodatnich. Należy więc znaleźć kres górny funkcji
przebiega zbiór wszystkich liczb dodatnich. Należy więc znaleźć kres górny funkcji 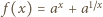 zmiennej
zmiennej 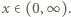 Ponieważ
Ponieważ 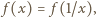 kres górny na przedziale
kres górny na przedziale 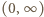 jest taki sam, jak na przedziale
jest taki sam, jak na przedziale 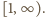 Pochodna funkcji
Pochodna funkcji 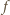 ma po prostym przekształceniu postać
ma po prostym przekształceniu postać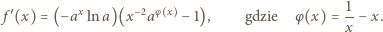
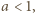 czynnik w pierwszym nawiasie jest stale dodatni. Czynnik w drugim nawiasie ma taki sam znak jak wyrażenie
czynnik w pierwszym nawiasie jest stale dodatni. Czynnik w drugim nawiasie ma taki sam znak jak wyrażenie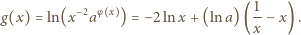
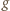 w przedziale
w przedziale 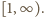 Jej pochodna:
Jej pochodna: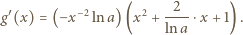
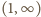 może być co najwyżej jeden pierwiastek. Dla dużych
może być co najwyżej jeden pierwiastek. Dla dużych 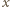 trójmian ma wartości dodatnie. Zatem wartości
trójmian ma wartości dodatnie. Zatem wartości 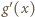 albo są dodatnie w całym przedziale
albo są dodatnie w całym przedziale 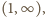 albo są - przedziałami - najpierw ujemne, potem dodatnie. Funkcja
albo są - przedziałami - najpierw ujemne, potem dodatnie. Funkcja 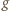 jest więc albo rosnąca, albo (kolejno) malejąca-rosnąca. A ponieważ
jest więc albo rosnąca, albo (kolejno) malejąca-rosnąca. A ponieważ 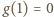 oraz
oraz 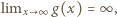 wynika stąd, że także wartości
wynika stąd, że także wartości 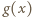 są albo stale dodatnie, albo (przedziałami, od lewej) ujemne-dodatnie.
są albo stale dodatnie, albo (przedziałami, od lewej) ujemne-dodatnie.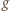 ma taki znak, jak
ma taki znak, jak 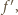 wobec czego możemy powtórzyć rozumowanie: funkcja
wobec czego możemy powtórzyć rozumowanie: funkcja 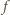 jest albo rosnąca, albo (kolejno) malejąca-rosnąca. W każdym przypadku jej kresem górnym na przedziale
jest albo rosnąca, albo (kolejno) malejąca-rosnąca. W każdym przypadku jej kresem górnym na przedziale 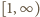 jest jej wartość lub granica w jednym z końców przedziału. Otrzymujemy wynik:
jest jej wartość lub granica w jednym z końców przedziału. Otrzymujemy wynik: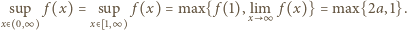
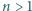 oraz dla dowolnych liczb rzeczywistych dodatnich
oraz dla dowolnych liczb rzeczywistych dodatnich 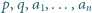 zachodzi nierówność
zachodzi nierówność
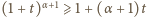 (słusznej dla
(słusznej dla 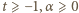 ) wykonujemy "przesunięcie zmiennej"
) wykonujemy "przesunięcie zmiennej" 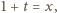 uzyskując postać
uzyskując postać
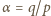 oraz
oraz 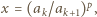 dostajemy
dostajemy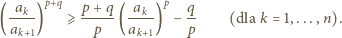
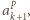 otrzymując
otrzymując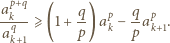
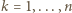 ) to teza zadania.
) to teza zadania.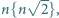 gdy
gdy 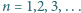
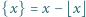 ).
).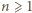 i oznaczmy
i oznaczmy 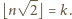 Oczywiście
Oczywiście 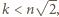 czyli
czyli 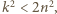 zatem
zatem 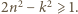 Dostajemy oszacowanie
Dostajemy oszacowanie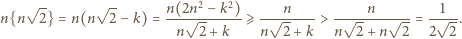
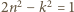 ; druga będzie "bliska równości", gdy stosunek
; druga będzie "bliska równości", gdy stosunek 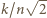 będzie bliski 1.
będzie bliski 1.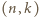 równania
równania 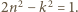 Para
Para 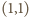 jest rozwiązaniem. Dalej, jeśli para
jest rozwiązaniem. Dalej, jeśli para 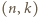 jest rozwiązaniem, to
jest rozwiązaniem, to 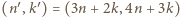 też, bowiem
też, bowiem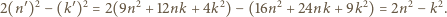
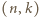 z dowolnie wielką wartością
z dowolnie wielką wartością 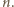 Gdy
Gdy 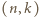 jest dowolną z takich par, wówczas
jest dowolną z takich par, wówczas 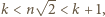 czyli
czyli 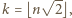 wobec czego (zgodnie z początkowym przekształceniem)
wobec czego (zgodnie z początkowym przekształceniem)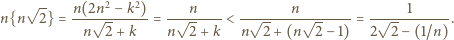
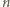 może być dowolnie wielka, zatem ostatnie wyrażenie może mieć wartość dowolnie bliską
może być dowolnie wielka, zatem ostatnie wyrażenie może mieć wartość dowolnie bliską 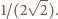 To dowodzi, że istotnie liczba
To dowodzi, że istotnie liczba 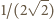 jest kresem dolnym zbioru wartości
jest kresem dolnym zbioru wartości 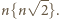
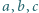 są rozwiązaniami równania
są rozwiązaniami równania 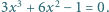 Obliczyć wartość
Obliczyć wartość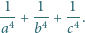
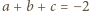 oraz
oraz 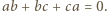 W takim razie mamy również
W takim razie mamy również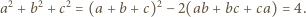
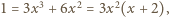 czyli
czyli 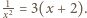 Stąd otrzymujemy
Stąd otrzymujemy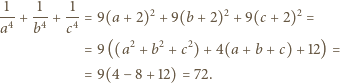
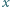 spełniająca równanie
spełniająca równanie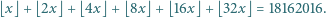
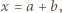 gdzie
gdzie 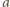 jest pewną liczbą całkowitą oraz
jest pewną liczbą całkowitą oraz 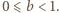 Lewa strona równania przyjmuje postać
Lewa strona równania przyjmuje postać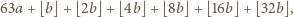
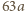 i nie większa niż
i nie większa niż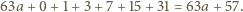
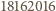 daje resztę
daje resztę 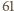 z dzielenia przez
z dzielenia przez 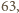 więc nie może być wartością lewej strony równania dla żadnego
więc nie może być wartością lewej strony równania dla żadnego 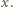
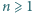 znaleźć najmniejszą liczbę rzeczywistą
znaleźć najmniejszą liczbę rzeczywistą  taką, że dla każdej liczby rzeczywistej
taką, że dla każdej liczby rzeczywistej 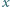 spełniona jest nierówność
spełniona jest nierówność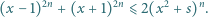
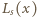 oraz
oraz 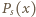 lewą oraz prawą stronę napisanej nierówności. Ponieważ
lewą oraz prawą stronę napisanej nierówności. Ponieważ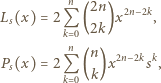
 (z parametrem
(z parametrem  )
)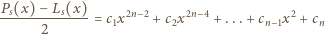
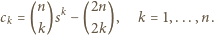
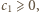 czyli
czyli 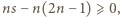 czyli
czyli 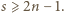
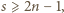 to wszystkie współczynniki
to wszystkie współczynniki 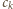 są nieujemne. Indukcja: baza
są nieujemne. Indukcja: baza 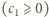 już gotowa. Ustalmy
już gotowa. Ustalmy 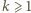 i przyjmijmy założenie indukcyjne
i przyjmijmy założenie indukcyjne 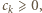 czyli
czyli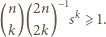
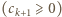 ma analogiczną postać, z
ma analogiczną postać, z 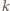 zastąpionym przez
zastąpionym przez 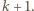 Piszemy więc to wyrażenie i zaczynamy je przekształcać:
Piszemy więc to wyrażenie i zaczynamy je przekształcać: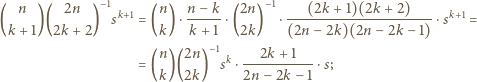
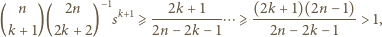
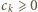 dla
dla 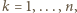 wobec czego
wobec czego 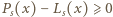 dla wszystkich
dla wszystkich 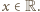
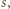 dla której
dla której 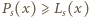 (dla
(dla 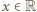 ), wynosi
), wynosi 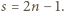
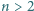 liczba
liczba 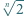 jest niewymierna.
jest niewymierna.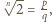 gdzie
gdzie 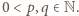 Wtedy
Wtedy 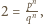 zatem
zatem 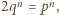 czyli
czyli 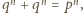 sprzecznie z Wielkim Twierdzeniem Fermata.
sprzecznie z Wielkim Twierdzeniem Fermata.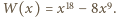 Wówczas
Wówczas 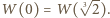 Przypuśćmy, że
Przypuśćmy, że 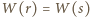 dla pewnych liczb wymiernych
dla pewnych liczb wymiernych 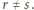 Równanie
Równanie 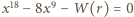 ma wtedy dwa różne pierwiastki wymierne
ma wtedy dwa różne pierwiastki wymierne 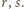 Stąd także równanie
Stąd także równanie 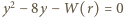 ma dwa różne pierwiastki wymierne
ma dwa różne pierwiastki wymierne 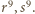 Wobec tego z wzorów Viète'a
Wobec tego z wzorów Viète'a 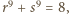 czyli
czyli 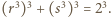
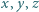 będą liczbami rzeczywistymi dodatnimi. Udowodnić, że
będą liczbami rzeczywistymi dodatnimi. Udowodnić, że
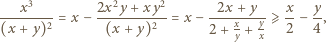

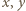 zachodzi
zachodzi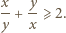
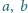 spełniają równania:
spełniają równania: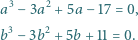
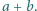
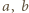 jako
jako 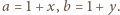 Wówczas
Wówczas
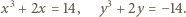
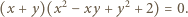
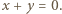 To daje odpowiedź:
To daje odpowiedź: 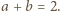
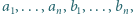 spełniających
spełniających 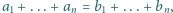 prawdziwa jest nierówność
prawdziwa jest nierówność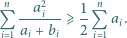
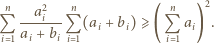
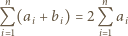
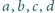 będą takimi liczbami rzeczywistymi, że
będą takimi liczbami rzeczywistymi, że
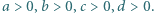
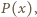 którego pierwiastkami są liczby
którego pierwiastkami są liczby 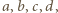 czyli
czyli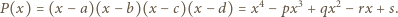
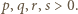 Jeżeli więc
Jeżeli więc 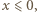 to oczywiście
to oczywiście 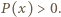 Widzimy zatem, że żaden z pierwiastków
Widzimy zatem, że żaden z pierwiastków 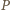 nie może być liczbą ujemną, co kończy rozwiązanie.
nie może być liczbą ujemną, co kończy rozwiązanie.
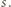 Udowodnimy najpierw, że liczba
Udowodnimy najpierw, że liczba  nie jest całkowita. Zauważmy w tym celu, że dla dowolnej liczby całkowitej
nie jest całkowita. Zauważmy w tym celu, że dla dowolnej liczby całkowitej 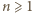 zachodzą nierówności
zachodzą nierówności


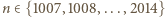 prawdziwe są nierówności
prawdziwe są nierówności
 nie jest liczbą całkowitą, gdyż część ułamkowa każdego z jej
nie jest liczbą całkowitą, gdyż część ułamkowa każdego z jej 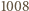 składników jest mniejsza niż
składników jest mniejsza niż 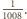 Dowodzi to naszego stwierdzenia.
Dowodzi to naszego stwierdzenia.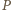 o współczynnikach całkowitych, taki, że
o współczynnikach całkowitych, taki, że 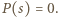 Stąd już natychmiast otrzymamy tezę zadania, gdyż z twierdzenia o pierwiastku wymiernym wynika, że każdy wymierny pierwiastek wielomianu
Stąd już natychmiast otrzymamy tezę zadania, gdyż z twierdzenia o pierwiastku wymiernym wynika, że każdy wymierny pierwiastek wielomianu 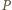 jest również całkowity. W szczególności, skoro
jest również całkowity. W szczególności, skoro 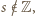 to tym samym
to tym samym 
 wykażemy ogólniejsze stwierdzenie: dla dowolnych liczb całkowitych
wykażemy ogólniejsze stwierdzenie: dla dowolnych liczb całkowitych 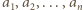 istnieje unormowany wielomian
istnieje unormowany wielomian 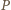 o współczynnikach całkowitych, dla którego
o współczynnikach całkowitych, dla którego
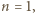 wystarczy przyjąć
wystarczy przyjąć 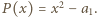 Załóżmy więc, że
Załóżmy więc, że 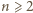 oraz istnieje wielomian unormowany
oraz istnieje wielomian unormowany 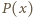 o współczynnikach całkowitych, dla którego
o współczynnikach całkowitych, dla którego 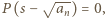 gdzie
gdzie 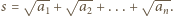 Przyjmijmy, że stopień wielomianu
Przyjmijmy, że stopień wielomianu 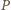 to
to  i że
i że 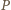 zapisuje się w postaci
zapisuje się w postaci 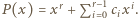 W szczególności
W szczególności

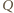 i
i 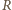 są wielomianami o współczynnikach całkowitych stopnia mniejszego niż
są wielomianami o współczynnikach całkowitych stopnia mniejszego niż 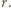 Przenosząc składnik
Przenosząc składnik 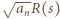 na drugą stronę i podnosząc obie strony równości do kwadratu, dostajemy
na drugą stronę i podnosząc obie strony równości do kwadratu, dostajemy
 jest pierwiastkiem unormowanego wielomianu
jest pierwiastkiem unormowanego wielomianu
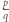

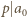
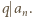
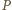
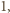
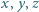 spełniają warunki
spełniają warunki