Trójmian kwadratowy»Zadanie 8
o zadaniu...
- Zadanie pochodzi z artykułu Trójmian kwadratowy
- Publikacja w Delcie: październik 2019
- Publikacja elektroniczna: 30 września 2019
- Artykuł źródłowy w wersji do druku [application/pdf]: (388 KB)
Funkcja kwadratowa 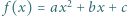 spełnia dla każdego
spełnia dla każdego ![|x∈ [−1,1]](/math/temat/matematyka/analiza/zadania/2019/09/30/zm-19_10-kpo-8/2x-74a6438c69d0f6ea8ca78cf3a770b01ff3c09138-im-2C,6B,73-FF,FF,FF.gif) nierówność
nierówność 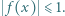 Wyznaczyć największą możliwą wartość wyrażenia
Wyznaczyć największą możliwą wartość wyrażenia 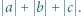
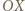 i
i 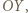 można założyć bez utraty ogólności, że
można założyć bez utraty ogólności, że 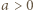 i
i 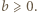 Jeśli
Jeśli 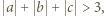 to
to 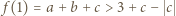 oraz
oraz 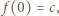 więc
więc 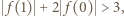 czyli
czyli 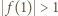 lub
lub 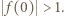 Wartość
Wartość 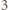 jest osiągalna, na przykład dla funkcji
jest osiągalna, na przykład dla funkcji 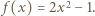
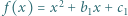 i
i 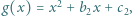 których współczynniki są rzeczywiste i spełniają warunek
których współczynniki są rzeczywiste i spełniają warunek
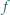 i
i 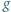 mają obydwa pierwiastki rzeczywiste, a każdy z nich ma jeden pierwiastek leżący na osi liczbowej pomiędzy pierwiastkami drugiego.
mają obydwa pierwiastki rzeczywiste, a każdy z nich ma jeden pierwiastek leżący na osi liczbowej pomiędzy pierwiastkami drugiego.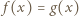 ma dokładnie jedno rozwiązanie
ma dokładnie jedno rozwiązanie 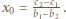 Wówczas
Wówczas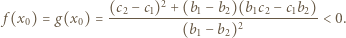
 i
i  przecinają się tylko w jednym punkcie, leżącym poniżej osi
przecinają się tylko w jednym punkcie, leżącym poniżej osi 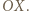 Resztę załatwia własność Darboux.
Resztę załatwia własność Darboux.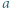 jest cyfrą setek,
jest cyfrą setek, 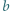 - cyfrą dziesiątek, a
- cyfrą dziesiątek, a  - cyfrą jedności, jest pierwsza. Dowieść, że
- cyfrą jedności, jest pierwsza. Dowieść, że 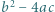 nie jest kwadratem liczby naturalnej.
nie jest kwadratem liczby naturalnej.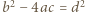 dla pewnej liczby naturalnej
dla pewnej liczby naturalnej 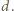 Niech
Niech 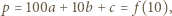 gdzie
gdzie 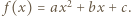 Korzystając z postaci iloczynowej, otrzymamy po przekształceniach
Korzystając z postaci iloczynowej, otrzymamy po przekształceniach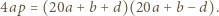
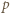 jest pierwsza, więc dzieli co najmniej jedną z liczb:
jest pierwsza, więc dzieli co najmniej jedną z liczb: 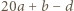 lub
lub 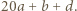 Tu mamy sprzeczność, bo są to liczby dodatnie mniejsze od
Tu mamy sprzeczność, bo są to liczby dodatnie mniejsze od 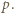
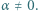 Funkcja
Funkcja 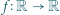 spełnia dla każdej pary liczb rzeczywistych
spełnia dla każdej pary liczb rzeczywistych 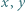 równanie
równanie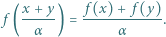
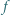 spełnia dla każdej pary liczb rzeczywistych
spełnia dla każdej pary liczb rzeczywistych 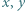 równanie
równanie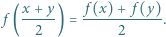
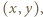 a drugi raz dla
a drugi raz dla 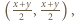 uzyskujemy
uzyskujemy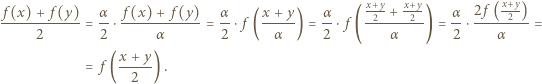
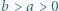 oraz parzystej liczby naturalnej
oraz parzystej liczby naturalnej 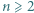 wyznaczyć kres górny wartości stosunku
wyznaczyć kres górny wartości stosunku 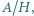 gdzie
gdzie 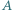 i
i 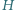 to (odpowiednio) średnia arytmetyczna i średnia harmoniczna
to (odpowiednio) średnia arytmetyczna i średnia harmoniczna 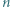 liczb wybranych dowolnie z przedziału
liczb wybranych dowolnie z przedziału ![[a,b].](/math/temat/matematyka/analiza/zadania/2019/04/29/zm-k44-781/7x-ef372a8dfa93edadbc34939244d39cca0f9e4c26-im-2C,6B,73-FF,FF,FF.gif)
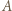 i
i 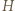 liczb
liczb ![x1, | ...,xn ∈[a,b].](/math/temat/matematyka/analiza/zadania/2019/04/29/zm-k44-781/3x-bed5f731d399079efabe3448810444f970457e80-im-66,57,43-FF,FF,FF.gif) Weźmy dowolną liczbę
Weźmy dowolną liczbę 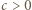 i zauważmy, że
i zauważmy, że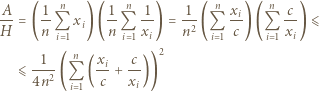
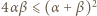 dla liczb
dla liczb 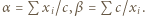
![x ∈ [a,b]](/math/temat/matematyka/analiza/zadania/2019/04/29/zm-k44-781/1x-2643bd4bae04ef39ab2c2805c88b5fc400e1fac5-im-66,57,43-FF,FF,FF.gif) mamy nierówność
mamy nierówność 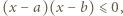 którą przepisujemy w postaci
którą przepisujemy w postaci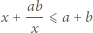
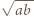 :
: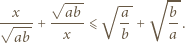
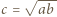 i korzystając z (2):
i korzystając z (2):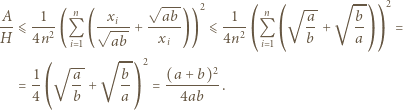
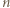 jest z założenia parzysta. Gdy
jest z założenia parzysta. Gdy 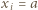 dla połowy spośród wskaźników
dla połowy spośród wskaźników 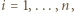 zaś
zaś 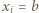 dla pozostałej połowy, wówczas we wszystkich szacowaniach zachodzi równość. Zatem liczba
dla pozostałej połowy, wówczas we wszystkich szacowaniach zachodzi równość. Zatem liczba 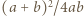 jest maksymalną wartością stosunku
jest maksymalną wartością stosunku 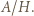
 prawdziwa jest nierówność
prawdziwa jest nierówność
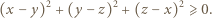

 i
i 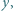 niebędących jednocześnie zerami.
niebędących jednocześnie zerami.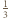 oraz
oraz 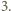 Rozwiązanie ułatwia spostrzeżenie, że szacowany ułamek ma dodatni licznik i mianownik, bo
Rozwiązanie ułatwia spostrzeżenie, że szacowany ułamek ma dodatni licznik i mianownik, bo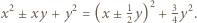
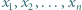 zachodzi nierówność
zachodzi nierówność
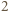 i przeniesieniu wszystkich wyrazów na lewą stronę nierówności otrzymamy
i przeniesieniu wszystkich wyrazów na lewą stronę nierówności otrzymamy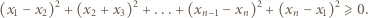

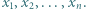
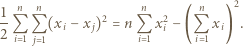
 jest równa
jest równa  Udowodnić, że
Udowodnić, że
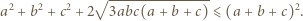
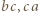 i
i 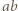 ułatwia dalsze rachunki.
ułatwia dalsze rachunki.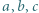 spełniają równość
spełniają równość 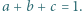 Wykazać, że
Wykazać, że
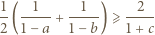
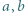 i
i  zachodzi nierówność
zachodzi nierówność
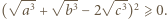
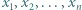 będą liczbami dodatnimi. Przyjmijmy
będą liczbami dodatnimi. Przyjmijmy 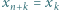 dla całkowitych
dla całkowitych 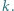 Dowieść, że prawdziwa jest co najmniej jedna z nierówności:
Dowieść, że prawdziwa jest co najmniej jedna z nierówności:
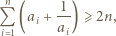
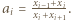
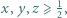 spełniających warunek
spełniających warunek 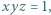 zachodzi nierówność
zachodzi nierówność
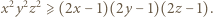
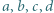 spełniają nierówność
spełniają nierówność
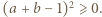
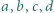 zachodzi nierówność
zachodzi nierówność
![x ,x ,...,x ∈ [−1,1] 1 2 n](/math/temat/matematyka/analiza/zadania/2019/04/29/zm-19_05-kpm-12/1x-e242253ed078688e97a06aead3aec19a78e70a97-im-2C,6B,73-FF,FF,FF.gif) spełniają warunek
spełniają warunek 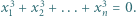 Dowieść, że
Dowieść, że
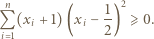
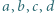 zachodzi nierówność
zachodzi nierówność

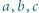 spełniają równości
spełniają równości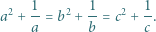
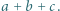
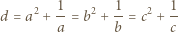
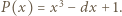 Skoro
Skoro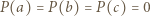
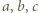 są różne, to są one różnymi pierwiastkami wielomianu
są różne, to są one różnymi pierwiastkami wielomianu 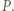 Stąd na mocy wzorów Viéte'a uzyskujemy
Stąd na mocy wzorów Viéte'a uzyskujemy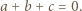
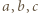 spełniające założenia zadania rzeczywiście istnieją, np.
spełniające założenia zadania rzeczywiście istnieją, np.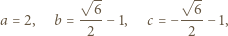
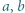 spełniają równość
spełniają równość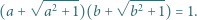
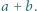
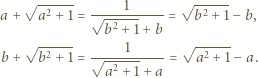
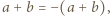 czyli
czyli 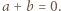
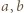 spełniające założenia zadania rzeczywiście istnieją (np.
spełniające założenia zadania rzeczywiście istnieją (np. 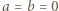 ), więc znaleziona wartość 0 istotnie jest osiągalna.
), więc znaleziona wartość 0 istotnie jest osiągalna.