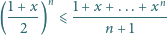Zadana nierówność zachodzi dla
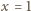 . Dla
. Dla
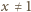 przepisujemy ją
równoważnie jako
przepisujemy ją
równoważnie jako
i w tej postaci będziemy jej dowodzić.
Dla każdej pary liczb rzeczywistych
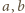 ma miejsce równość
ma miejsce równość
gdzie
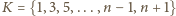 . Kontynuujemy przekształcenia dla
. Kontynuujemy przekształcenia dla
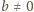 :
:
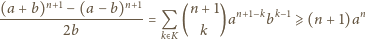 | (2) |
ostatnia nierówność powstała przez odrzucenie z uzyskanej sumy wszystkich
składników z wyjątkiem pierwszego – są one liczbami nieujemnymi, bo
wykładniki potęg są parzyste.
Podstawiamy teraz w (2)
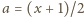 ,
,
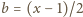 i dostajemy
dowodzoną nierówność (1).
i dostajemy
dowodzoną nierówność (1).
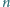 oraz dla każdej
liczby rzeczywistej
oraz dla każdej
liczby rzeczywistej
 zachodzi nierówność
zachodzi nierówność