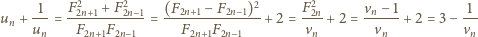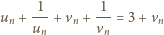Matematyka jest jedna: wielomiany mogą wszystko»Zadanie 6
o zadaniu...
- Zadanie pochodzi z artykułu Matematyka jest jedna: wielomiany mogą wszystko
- Publikacja w Delcie: wrzesień 2015
- Publikacja elektroniczna: 31-08-2015
Dane jest 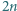 parami różnych liczb rzeczywistych
parami różnych liczb rzeczywistych  oraz tablica
oraz tablica  W pole leżące w
W pole leżące w 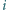 -tym wierszu i w
-tym wierszu i w 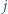 -tej kolumnie wpisano liczbę
-tej kolumnie wpisano liczbę 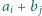 dla
dla 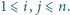 Udowodnić, że jeżeli iloczyny liczb we wszystkich kolumnach są równe, to również iloczyny liczb we wszystkich wierszach są równe.
Udowodnić, że jeżeli iloczyny liczb we wszystkich kolumnach są równe, to również iloczyny liczb we wszystkich wierszach są równe.
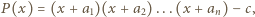 gdzie
gdzie  jest wartością wspólną iloczynów liczb w kolumnach.
jest wartością wspólną iloczynów liczb w kolumnach.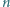 oraz liczb rzeczywistych
oraz liczb rzeczywistych  spełniających
spełniających 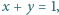 prawdziwa jest tożsamość
prawdziwa jest tożsamość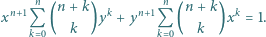
![x ∈[0,1]](/math/temat/matematyka/analiza/zadania/2015/06/29/zm-1463/1x-334d5fb9c059ea46c340b1dc0cd157b4566f8db6-im-66,57,43-FF,FF,FF.gif) i rozważmy doświadczenie losowe polegające na rzucaniu monetą tak długo, dopóki
i rozważmy doświadczenie losowe polegające na rzucaniu monetą tak długo, dopóki 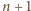 razy wypadnie orzeł lub
razy wypadnie orzeł lub  razy reszka. Prawdopodobieństwo wypadnięcia orła w pojedynczym rzucie wynosi
razy reszka. Prawdopodobieństwo wypadnięcia orła w pojedynczym rzucie wynosi 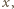 zaś reszki
zaś reszki 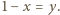 Zauważmy, że prawdopodobieństwo tego, że doświadczenie zakończy się w rzucie
Zauważmy, że prawdopodobieństwo tego, że doświadczenie zakończy się w rzucie 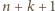 (dla
(dla 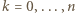 ) z powodu wypadnięcia
) z powodu wypadnięcia 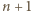 orłów wynosi
orłów wynosi  a z powodu wypadnięcia
a z powodu wypadnięcia 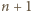 reszek -
reszek - 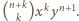 Sumując prawdopodobieństwa poszczególnych możliwości zakończenia doświadczenia, otrzymujemy
Sumując prawdopodobieństwa poszczególnych możliwości zakończenia doświadczenia, otrzymujemy
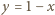 lewa strona tożsamości jest wielomianem zmiennej
lewa strona tożsamości jest wielomianem zmiennej 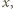 który jest tożsamościowo równy
który jest tożsamościowo równy 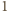 na przedziale
na przedziale ![|[0,1],](/math/temat/matematyka/analiza/zadania/2015/06/29/zm-1463/16x-334d5fb9c059ea46c340b1dc0cd157b4566f8db6-im-66,57,43-FF,FF,FF.gif) więc jest on równy
więc jest on równy 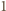 dla wszystkich
dla wszystkich 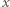 rzeczywistych.
rzeczywistych.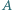 oraz najmniejszą liczbę
oraz najmniejszą liczbę 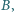 takie że dla każdej czwórki liczb rzeczywistych
takie że dla każdej czwórki liczb rzeczywistych 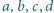 spełniona jest nierówność
spełniona jest nierówność
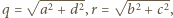
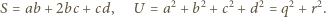
 oraz
oraz 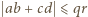 (nier. Cauchy'ego-Schwarza), zatem
(nier. Cauchy'ego-Schwarza), zatem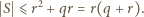
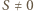 (więc
(więc 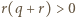 ). Wówczas
). Wówczas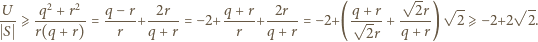

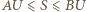 zachodzi ze stałymi
zachodzi ze stałymi 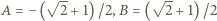 (dla
(dla 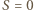 oczywiście też).
oczywiście też).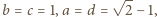 uzyskujemy równość
uzyskujemy równość 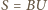 (z podaną stałą
(z podaną stałą  ); zaś zmieniając znak w
); zaś zmieniając znak w  i
i 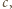 dostajemy równość
dostajemy równość 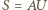 (z podaną stałą
(z podaną stałą  ). Znalezione stałe są więc optymalne.
). Znalezione stałe są więc optymalne.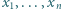 będą liczbami rzeczywistymi dodatnimi, przy czym
będą liczbami rzeczywistymi dodatnimi, przy czym 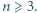 Dla wygody przyjmijmy dodatkowo, że
Dla wygody przyjmijmy dodatkowo, że 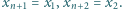
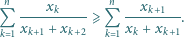
 jest monotoniczny, to
jest monotoniczny, to

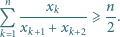
 dla
dla 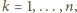 wynosi
wynosi 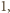 to korzystając z nierówności między średnimi, dostajemy
to korzystając z nierówności między średnimi, dostajemy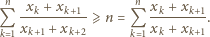
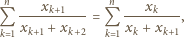
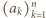 i
i 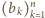 spełniają
spełniają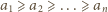
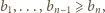
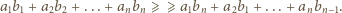
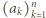 i
i 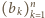 spełniają
spełniają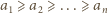


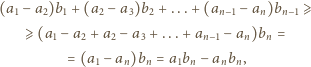
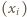 jest nierosnący:
jest nierosnący:
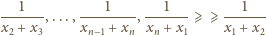
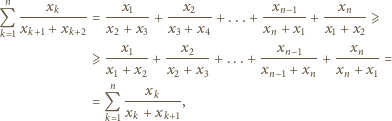
 jest niemalejący, postępujemy analogicznie.
jest niemalejący, postępujemy analogicznie.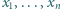 będą liczbami rzeczywistymi dodatnimi, przy czym
będą liczbami rzeczywistymi dodatnimi, przy czym 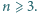 Dla wygody przyjmijmy dodatkowo, że
Dla wygody przyjmijmy dodatkowo, że 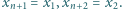 Udowodnić, że
Udowodnić, że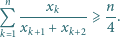
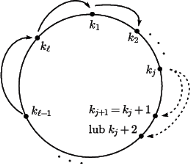
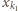 oznacza największą z liczb
oznacza największą z liczb 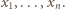 Popatrzmy na wyraz
Popatrzmy na wyraz 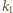 naszej sumy:
naszej sumy:
 lub
lub 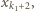 przez
przez 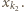 Popatrzmy teraz na wyraz
Popatrzmy teraz na wyraz 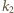 naszej sumy:
naszej sumy: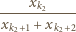
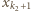 lub
lub 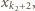 przez
przez  Kontynuując to postępowanie, otrzymujemy ciąg indeksów
Kontynuując to postępowanie, otrzymujemy ciąg indeksów 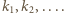
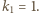 Z definicji mamy
Z definicji mamy 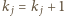 lub
lub 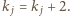 Zatem po pewnej liczbie kroków po raz pierwszy otrzymamy
Zatem po pewnej liczbie kroków po raz pierwszy otrzymamy 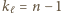 lub
lub 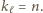 Ponadto
Ponadto 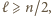 bo w każdym kroku przesuwamy się o co najwyżej dwa. Zauważmy też, że
bo w każdym kroku przesuwamy się o co najwyżej dwa. Zauważmy też, że 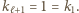

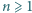 znaleźć wartość sumy
znaleźć wartość sumy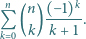
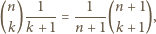
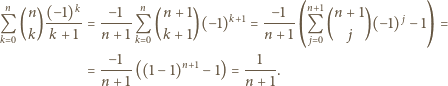
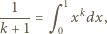
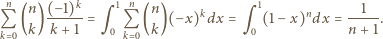
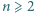 znaleźć najmniejszą wartość sumy
znaleźć najmniejszą wartość sumy
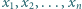 są dowolnymi liczbami rzeczywistymi dodatnimi, spełniającymi warunek
są dowolnymi liczbami rzeczywistymi dodatnimi, spełniającymi warunek 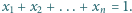
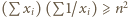 ; we wszystkich symbolach sumowania przyjmujemy
; we wszystkich symbolach sumowania przyjmujemy 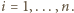 Przy warunku
Przy warunku 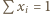 mamy więc
mamy więc  Dla każdej liczby rzeczywistej
Dla każdej liczby rzeczywistej  słuszne jest oszacowanie
słuszne jest oszacowanie 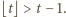 Stąd
Stąd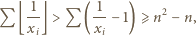
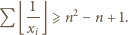
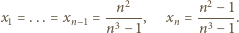
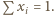 Dla
Dla 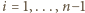 mamy przy tym
mamy przy tym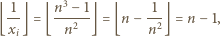
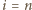 :
: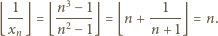
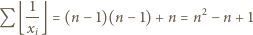
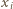 ; można dać wiele innych przykładów). Wniosek: liczba
; można dać wiele innych przykładów). Wniosek: liczba 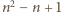 to szukane minimum.
to szukane minimum.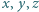 prawdziwa jest nierówność
prawdziwa jest nierówność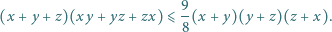

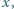 które spełniają równanie
które spełniają równanie 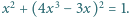
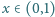 oraz dowolnych dodatnich liczb całkowitych
oraz dowolnych dodatnich liczb całkowitych 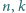 zachodzi nierówność
zachodzi nierówność

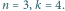
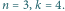
 wierszach i
wierszach i 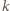 kolumnach, której każde pole pomalowano na czarno z prawdopodobieństwem
kolumnach, której każde pole pomalowano na czarno z prawdopodobieństwem 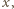 a z prawdopodobieństwem
a z prawdopodobieństwem 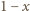 pozostawiono białe. Prawdopodobieństwo, że wybrany wiersz jest cały czarny jest wówczas równe
pozostawiono białe. Prawdopodobieństwo, że wybrany wiersz jest cały czarny jest wówczas równe 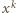 (bo każde z
(bo każde z 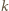 pól musi być czarne), więc prawdopodobieństwo, że istnieje w nim białe pole wynosi
pól musi być czarne), więc prawdopodobieństwo, że istnieje w nim białe pole wynosi 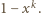
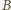 oznacza zdarzenie: w każdym wierszu jest co najmniej jedno białe pole. Wierszy jest
oznacza zdarzenie: w każdym wierszu jest co najmniej jedno białe pole. Wierszy jest  ; wobec powyższej obserwacji
; wobec powyższej obserwacji 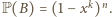 Analogicznie niech
Analogicznie niech 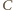 oznacza zdarzenie: w każdej kolumnie istnieje pole czarne, wówczas
oznacza zdarzenie: w każdej kolumnie istnieje pole czarne, wówczas 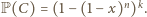
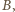 czyli nie jest prawdą, że w każdym wierszu jest białe pole, to istnieje wiersz o wszystkich polach czarnych. Wtedy na pewno w każdej kolumnie jest czarne pole (choćby z tego właśnie wiersza), czyli zachodzi zdarzenie
czyli nie jest prawdą, że w każdym wierszu jest białe pole, to istnieje wiersz o wszystkich polach czarnych. Wtedy na pewno w każdej kolumnie jest czarne pole (choćby z tego właśnie wiersza), czyli zachodzi zdarzenie 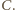 Wobec tego zawsze zachodzi co najmniej jedno spośród zdarzeń
Wobec tego zawsze zachodzi co najmniej jedno spośród zdarzeń 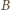 i
i 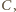 stąd
stąd 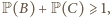 czyli
czyli 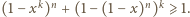
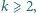
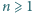 oraz
oraz 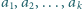 i
i  że
że 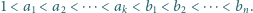 Wykazać, że jeżeli
Wykazać, że jeżeli 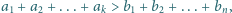 to
to 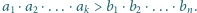
 dla
dla  Udowodnimy, że
Udowodnimy, że 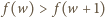 dla każdego
dla każdego 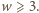 Bezpośrednie wymnożenie wskazuje, że
Bezpośrednie wymnożenie wskazuje, że 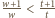 dla
dla 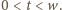 Zatem
Zatem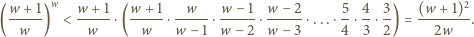
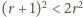 dla
dla 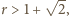 więc
więc  W efekcie
W efekcie 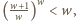 co jest równoważne nierówności
co jest równoważne nierówności 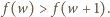 Ponieważ
Ponieważ  więc z zależności
więc z zależności 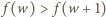 i związku
i związku 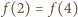 otrzymujemy
otrzymujemy 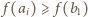 dla
dla 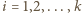 oraz
oraz  dla
dla  W myśl określenia funkcji
W myśl określenia funkcji  powyższe nierówności można zapisać w postaci
powyższe nierówności można zapisać w postaci 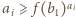 dla
dla 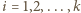 oraz
oraz 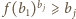 dla
dla 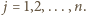 Stąd zaś, po wymnożeniu stronami i skorzystaniu z warunku (1), uzyskujemy
Stąd zaś, po wymnożeniu stronami i skorzystaniu z warunku (1), uzyskujemy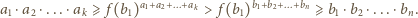
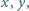 że
że  Oblicz
Oblicz 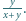
 skąd otrzymujemy
skąd otrzymujemy 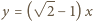 i podstawiamy:
i podstawiamy: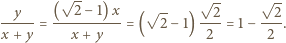
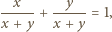
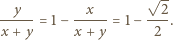
 będą liczbami dodatnimi i niech
będą liczbami dodatnimi i niech
 oznacza sumę
wszystkich iloczynów różnych
oznacza sumę
wszystkich iloczynów różnych
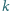 liczb spośród
liczb spośród
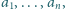

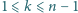 spełniona jest
nierówność
spełniona jest
nierówność
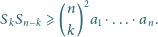
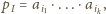 gdzie
gdzie
 jest ciągiem indeksów
jest ciągiem indeksów
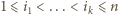 (mamy
(mamy
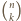 takich ciągów). Niech również
takich ciągów). Niech również
 Wówczas
Wówczas
 oraz
oraz
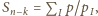 więc
z nierówności Schwarza dostajemy
więc
z nierówności Schwarza dostajemy
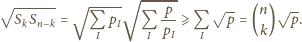
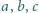 spełniające zależność
spełniające zależność
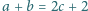 nie były tego samego
koloru?
nie były tego samego
koloru?
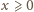 kolorujemy na kolor o numerze
kolorujemy na kolor o numerze
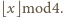 Załóżmy, że
Załóżmy, że
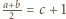 dla pewnych liczb
nieujemnych
dla pewnych liczb
nieujemnych
 i przyjmijmy, że
i przyjmijmy, że
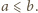 Załóżmy,
że
Załóżmy,
że
 i
i
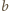 mają ten sam kolor. Niech
mają ten sam kolor. Niech
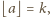 czyli
czyli
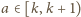 dla pewnej liczby całkowitej
dla pewnej liczby całkowitej
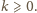 Wówczas
Wówczas
 dla pewnej liczby całkowitej
dla pewnej liczby całkowitej
 Zatem
Zatem
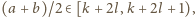 więc
więc
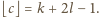 Ponieważ
Ponieważ
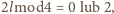 więc liczba
więc liczba
 ma w opisanym przez nas
kolorowaniu inny kolor niż liczby
ma w opisanym przez nas
kolorowaniu inny kolor niż liczby
 i
i
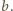
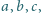 spełniające
spełniające
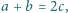 nie były tego samego koloru? Czy można pokolorować
w taki sposób zbiór liczb całkowitych nieujemnych?
nie były tego samego koloru? Czy można pokolorować
w taki sposób zbiór liczb całkowitych nieujemnych?
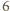 jest
biała. Jedna z liczb
jest
biała. Jedna z liczb
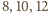 też musi być biała. Nazwijmy
ją
też musi być biała. Nazwijmy
ją
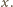 Wówczas liczby
Wówczas liczby
 i
i
 muszą być czarne.
Zatem ich średnia
muszą być czarne.
Zatem ich średnia
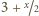 musi być biała. Dostaliśmy więc trzy białe
liczby
musi być biała. Dostaliśmy więc trzy białe
liczby
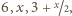 co daje sprzeczność.
co daje sprzeczność.
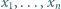 spełniają warunek
spełniają warunek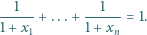
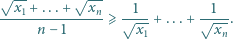
 Nierówność daną do udowodnienia przepisujemy w równoważnej postaci
Nierówność daną do udowodnienia przepisujemy w równoważnej postaci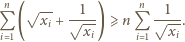
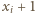 :
: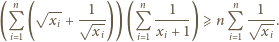
 i
i 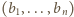 o wyrazach
o wyrazach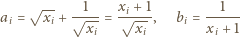
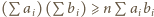 da wówczas dowodzoną tezę
da wówczas dowodzoną tezę 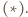
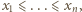 więc ciąg
więc ciąg 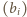 jest nierosnący; chcemy pokazać, że ciąg
jest nierosnący; chcemy pokazać, że ciąg  jest niemalejący. Funkcja
jest niemalejący. Funkcja 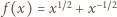 maleje w przedziale
maleje w przedziale 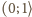 oraz rośnie w przedziale
oraz rośnie w przedziale 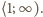 Zatem fragment ciągu
Zatem fragment ciągu 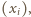 który leży w przedziale
który leży w przedziale 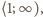 wyznacza niemalejący fragment ciągu o wyrazach
wyznacza niemalejący fragment ciągu o wyrazach 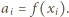 Skoro jednak
Skoro jednak 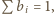 to w przedziale
to w przedziale 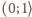 może leżeć co najwyżej jeden wyraz ciągu
może leżeć co najwyżej jeden wyraz ciągu 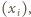 czyli liczba
czyli liczba 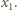 Pozostaje dowieść, że wówczas
Pozostaje dowieść, że wówczas 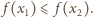 Z założenia
Z założenia 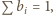 więc
więc 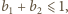 skąd (po prostym przekształceniu)
skąd (po prostym przekształceniu) 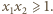 Stąd, ostatecznie,
Stąd, ostatecznie,
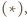 równoważnej z tezą zadania.
równoważnej z tezą zadania.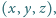 spełniające
warunki
spełniające
warunki

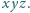

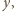
 muszą być różne od zera. Przepisujemy
pierwsze równanie jako
muszą być różne od zera. Przepisujemy
pierwsze równanie jako
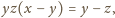 i dalej (cyklicznie)
i dalej (cyklicznie)
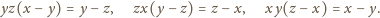

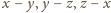 była zerem, to wobec
zależności (1) wszystkie byłyby zerami, czyli liczby
była zerem, to wobec
zależności (1) wszystkie byłyby zerami, czyli liczby

 byłyby równe. To się jednak kłóci z nierównością, daną
w założeniach. Różnice te są więc różne od zera. Równanie (2) po
skróceniu daje wynik:
byłyby równe. To się jednak kłóci z nierównością, daną
w założeniach. Różnice te są więc różne od zera. Równanie (2) po
skróceniu daje wynik:
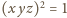 ; jedynymi możliwymi wartościami
iloczynu
; jedynymi możliwymi wartościami
iloczynu
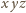 są liczby
są liczby
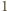 oraz
oraz
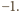 Każda z nich jest
faktycznie osiągalna – na przykład dla
Każda z nich jest
faktycznie osiągalna – na przykład dla
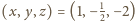 oraz
oraz
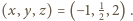
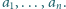 Niech
Niech
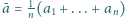 oznacza
ich średnią arytmetyczną. Udowodnić, że prawdziwa jest nierówność
oznacza
ich średnią arytmetyczną. Udowodnić, że prawdziwa jest nierówność
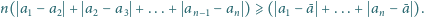
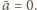 Wówczas
Wówczas

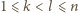 mamy
mamy
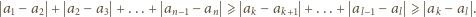
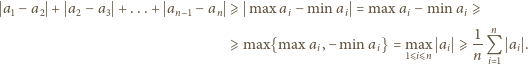
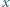 spełnia nierówność
spełnia nierówność
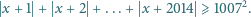
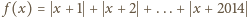 jest
kawałkami liniowa i ograniczona z dołu przez
jest
kawałkami liniowa i ograniczona z dołu przez
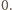 W takim razie przyjmuje
minimum w jednym z węzłów
W takim razie przyjmuje
minimum w jednym z węzłów
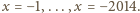 Nietrudno
sprawdzić, że jest to
Nietrudno
sprawdzić, że jest to
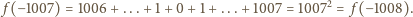
 dla których liczba
dla których liczba

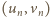 możemy uzyskać na przykład
biorąc ciąg Fibonacciego
możemy uzyskać na przykład
biorąc ciąg Fibonacciego
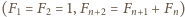 i określając
i określając
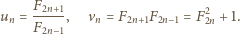
 mamy wówczas
mamy wówczas