Jedno z fundamentalnych stwierdzeń współczesnej astronomii zakłada, że gwiazdy powstają w zimnym gęstym gazie molekularnym. Wszystkie modele tworzenia i ewolucji galaktyk, które przecież składają się między innymi z milionów gwiazd, oparte są bezpośrednio na tym założeniu. Wspierane jest ono przez obserwacje astronomiczne, które wskazują, że galaktyki aktywnie tworzące gwiazdy - zazwyczaj spiralne o niebieskim kolorze - posiadają duże zapasy zimnego gazu molekularnego, przez co szybka produkcja gwiazd może być w nich podtrzymywana. Z kolei w drugiej klasie galaktyk, charakteryzujących się kolorem czerwonym, produkcja gwiazd zanikła i wypełniają je jedynie stare gwiazdy, będące u schyłku swojego życia.

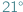 do
do 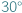 , w związku z czym czas jego przybywania na nieboskłonie wzrośnie prawie do 11 godzin...
, w związku z czym czas jego przybywania na nieboskłonie wzrośnie prawie do 11 godzin...