Kontynuując naszą przygodę z nieskończonością, spróbujmy wypracować podstawowe narzędzia do jej badania. Przyda nam się w tym celu pewna analogia pomiędzy zbiorami nieskończonymi a tymi skończonymi. Wyobraźmy sobie dwa skończone zbiory osób. Powiedzmy, że elementami pierwszego z nich są: Aldona, Balbina, Cezaria oraz Delfina, a elementami drugiego: Abelard, Baldwin, Cyryl oraz Dezyderiusz. Od razu zauważamy, że te zbiory mają tyle samo elementów. Jak dojść do tego wniosku? Można policzyć elementy w każdym ze zbiorów i w obu przypadkach wyjdzie cztery. A co by było, gdybyśmy nie umieli liczyć do czterech? Czy jest inna metoda pozwalająca na stwierdzenie, że te zbiory mają tyle samo elementów?


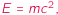
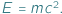 Pora to zmienić. Przytoczę jedno z najprostszych wyprowadzeń. Opowiem też, jak wspaniale astronomia i fizyka pomogły sobie nawzajem w czasach Einsteina. Dzięki temu rozumiemy, jak Słońce nas oświetla i ogrzewa i jak długo jeszcze będzie to robić.
Pora to zmienić. Przytoczę jedno z najprostszych wyprowadzeń. Opowiem też, jak wspaniale astronomia i fizyka pomogły sobie nawzajem w czasach Einsteina. Dzięki temu rozumiemy, jak Słońce nas oświetla i ogrzewa i jak długo jeszcze będzie to robić.