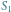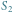1, 2, 3, 4, ...
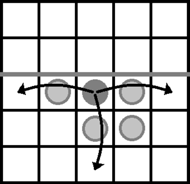
Rys. 1 Możliwe ruchy ciemnoszarego pionka
Conway's Soldiers to jednoosobowa łamigłówka, w której żołnierze (pionki) przedostają się na terytorium wroga i chcą wkroczyć jak najdalej. Na nieskończonej szachownicy, z zaznaczoną "na środku" poziomą granicą, pionki przeskakują jeden nad drugim. Dokładniej: ruch polega na przeskoczeniu pionkiem nad innym znajdującym się na sąsiadującym polu - tylko poziomo lub pionowo - i zdjęciu pionka, który został przeskoczony.
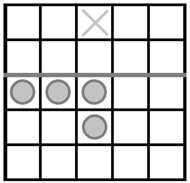
Rys. 2 Konfiguracja pionków, z której można dotrzeć do pola zaznaczonego krzyżykiem.
Początkowo wszystkie pionki ustawione są poniżej granicy (na rysunkach zaznaczona na szaro). Celem gry jest dostać się jak najdalej poza granicę. Należy znaleźć takie początkowe ustawienia pionków (dowolnie wielu), żeby przynajmniej jeden mógł znaleźć się 1, 2, 3, 4,... pola za granicą. Rysunek 2 przedstawia ustawienie, które umożliwia przekroczenie granicy o 2 pola. Zadanie: ile najmniej pionków jest potrzebnych, żeby przedostać się o 3 i 4 pola od granicy, pozostawiamy Czytelnikowi. Żeby zmierzyć się z problemem, wytoczymy oręże, jakim są półniezmienniki. Niezmiennikiem nazywamy pewną własność, która nie ulega zmianie podczas wykonywania procesu (przykład tutaj). Natomiast półniezmiennik to własność zmieniająca się w ściśle określony sposób (na przykład nie rośnie lub nie maleje).

Rys. 3
Ciekawe zadania o niezmiennikach i półniezmiennikach można znaleźć w artykułach K. Chełmińskiego i W. Pompego (Delta 07/1996, Delta 08/1996). O niezmienniku do badania węzłów jest artykuł J. Gładysza (Delta 01/2018).
Polom szachownicy przypiszemy wartości liczbowe i po każdym ruchu będziemy sumować liczby na zajętych polach. Chcemy znaleźć takie wartości, żeby ta suma (nazwijmy ją wartością gry) pozostawała stała lub żeby malała po każdym ruchu. Zauważmy, że jeden ruch powoduje, że na planszy jest o jeden pionek mniej, tak że wymaganie nie jest całkiem sztuczne.
Oznaczmy jedynką pole, do którego chcemy dotrzeć - nasz cel. Pozostałym polom przypiszmy 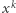 (dla każdego
(dla każdego 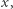 który ustalimy później) w taki sposób, że
który ustalimy później) w taki sposób, że 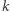 jest liczbą wierszy i kolumn, o które to pole jest odległe od "1" (Rys. 3).
jest liczbą wierszy i kolumn, o które to pole jest odległe od "1" (Rys. 3).
Możemy wyróżnić trzy typy ruchów w grze (poniżej zakładamy, że pionek skaczący startuje z pola 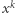 ):
):
- 1.
- Przybliżający do "1" - gdy pionek skaczący zbliża się do pola 1. Wartość gry zmieni się wtedy o
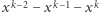 (
( 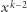 to pole, na którym wylądował pionek skaczący, a
to pole, na którym wylądował pionek skaczący, a 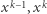 to pola, z których zniknęły pionki).
to pola, z których zniknęły pionki). - 2.
- Neutralny - pionek skaczący pozostaje w tej samej odległości od "1" co przed skokiem. Wartość gry zmienia się o
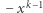 (pole, na którym stał przeskoczony pionek).
(pole, na którym stał przeskoczony pionek). - 3.
- Oddalający od "1" - wartość gry zmienia się o
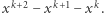
Sprecyzujmy wymagania wobec 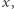 żeby wartość gry nie zmieniała się wtedy, gdy przybliżamy się do "1", czyli rozwiążmy dla
żeby wartość gry nie zmieniała się wtedy, gdy przybliżamy się do "1", czyli rozwiążmy dla 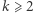 równanie
równanie
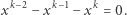 |
(*) |
Mamy dwóch kandydatów 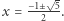 Jeden jest zdecydowanie lepszy od drugiego. Dla ujemnej wartości
Jeden jest zdecydowanie lepszy od drugiego. Dla ujemnej wartości 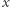 ruch neutralny może powodować zwiększanie wartości gry, a przecież tego nie chcieliśmy. Inny powód jest taki, że w dalszej części będziemy się starali wypełnić pionkami cały nieskończony wiersz szachownicy, co w przypadku, gdy
ruch neutralny może powodować zwiększanie wartości gry, a przecież tego nie chcieliśmy. Inny powód jest taki, że w dalszej części będziemy się starali wypełnić pionkami cały nieskończony wiersz szachownicy, co w przypadku, gdy 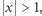 oznaczałoby sumowanie nieskończonego ciągu geometrycznego, o ilorazie większym niż 1. Kłopotliwie… Bezpieczniej jest wybrać
oznaczałoby sumowanie nieskończonego ciągu geometrycznego, o ilorazie większym niż 1. Kłopotliwie… Bezpieczniej jest wybrać 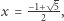 oznaczmy tę wartość przez
oznaczmy tę wartość przez 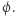 Zauważmy, że
Zauważmy, że 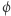 spełnia wcześniejsze wymaganie o tym, że w każdym ruchu wartość gry nie może wzrastać - wartość gry maleje, gdy wykonujemy ruch oddalający
spełnia wcześniejsze wymaganie o tym, że w każdym ruchu wartość gry nie może wzrastać - wartość gry maleje, gdy wykonujemy ruch oddalający 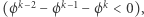 przy ruchu neutralnym również.
przy ruchu neutralnym również.

Rys. 4 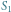
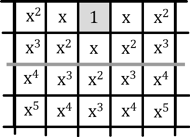
Rys. 5 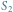
Zachodzą następujące równości

Z powyższego otrzymujemy 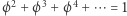 (dodaliśmy prawe i lewe strony powyższych równań). Mamy również
(dodaliśmy prawe i lewe strony powyższych równań). Mamy również

Mając planszę ponumerowaną konkretnymi liczbami i znając parę zależności dla tych wartości, obliczmy wartość gry w sytuacji, gdyby wszystkie pola (czyli nieskończenie wiele!) poniżej granicy były zajęte przez pionki, a naszym celem byłoby dostanie się tuż nad granicę (Rys. 4). Oznaczmy wartość takiej konfiguracji przez 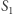

Korzystając z tego, że 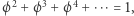 dostajemy
dostajemy

gdyż 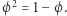
Teraz jako cel wyznaczmy sobie pole oddalone od granicy o dwa i ponownie zapełnijmy pionkami wszystkie pola poniżej granicy

Analogicznie

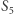 to wartość gry w przypadku, gdy naszym celem jest dojście do pola oddalonego od granicy o 5, ma to, oczywiście, związek z początkowym pytaniem. Ponieważ i tak wypełniamy wszystkie pola poniżej granicy na nieskończonej szachownicy, to ulokowanie "1" w tym czy w innym miejscu (ale 5 pól od granicy) niczego nie zmienia.
to wartość gry w przypadku, gdy naszym celem jest dojście do pola oddalonego od granicy o 5, ma to, oczywiście, związek z początkowym pytaniem. Ponieważ i tak wypełniamy wszystkie pola poniżej granicy na nieskończonej szachownicy, to ulokowanie "1" w tym czy w innym miejscu (ale 5 pól od granicy) niczego nie zmienia.
Cóż wynika z tego, że 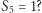 Oznacza to tyle, że w tej grze nie da się dojść pionkami na żadne pole oddalone od granicy o 5! Dla skończonej liczby pionków wartość początkowej konfiguracji będzie mniejsza niż 1, a ponieważ wartość nie może wzrosnąć po ruchu (tak dobraliśmy wartość
Oznacza to tyle, że w tej grze nie da się dojść pionkami na żadne pole oddalone od granicy o 5! Dla skończonej liczby pionków wartość początkowej konfiguracji będzie mniejsza niż 1, a ponieważ wartość nie może wzrosnąć po ruchu (tak dobraliśmy wartość 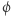 ), to startując z ustawienia o wartości mniejszej niż 1, nigdy nie osiągniemy pola "1".
), to startując z ustawienia o wartości mniejszej niż 1, nigdy nie osiągniemy pola "1".