Zadanie to ma ładne rozwiązanie, bardzo ładne uogólnienie i nie jest mi znane
jego rozwiązanie w przypadku najbardziej ogólnym. Przestawiając pierwszy lub
ostatni pionek na początek planszy, pierwszy gracz może łatwo sprowadzić grę
do planszy parzystej długości z dwoma pionkami na końcu z sobą jako
drugim graczem. Jeżeli teraz podzieli planszę na „szufladki” po dwa kolejne
pola i po każdym ruchu pionkiem swojego przeciwnika będzie przekładał
drugi pionek do tej samej szufladki co przeciwnik, to zwycięstwo ma w kieszeni.
Stosując tę samą metodę, można rozstrzygnąć losy gry ogólniejszej: gdy
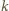 pionków stoi na końcowych polach planszy. Jeżeli zarówno
pionków stoi na końcowych polach planszy. Jeżeli zarówno
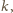 jak i
jak i
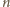 są parzyste, to dzieląc planszę na takie same szufladki
i przestawiając po każdym ruchu pierwszego gracza drugi pionek z szufladki,
w której stał pionek ruszony przez gracza pierwszego, do tej szufladki, do
której pierwszy gracz wstawił pionek, drugi gracz zapewni sobie zwycięstwo.
Jeżeli
są parzyste, to dzieląc planszę na takie same szufladki
i przestawiając po każdym ruchu pierwszego gracza drugi pionek z szufladki,
w której stał pionek ruszony przez gracza pierwszego, do tej szufladki, do
której pierwszy gracz wstawił pionek, drugi gracz zapewni sobie zwycięstwo.
Jeżeli
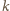 jest parzyste, a
jest parzyste, a
 nieparzyste – pierwszy gracz,
przestawiając ostatni pionek tuż przed pionek pierwszy, sprowadzi grę do
przypadku już rozważonego z sobą w roli drugiego, a więc wygra. Jeżeli
zaś
nieparzyste – pierwszy gracz,
przestawiając ostatni pionek tuż przed pionek pierwszy, sprowadzi grę do
przypadku już rozważonego z sobą w roli drugiego, a więc wygra. Jeżeli
zaś
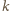 jest nieparzyste, to pierwszy gracz, przestawiając, w zależności
od parzystości
jest nieparzyste, to pierwszy gracz, przestawiając, w zależności
od parzystości
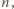 pierwszy bądź ostatni z pionków, zawsze może
sprowadzić grę do przypadku
pierwszy bądź ostatni z pionków, zawsze może
sprowadzić grę do przypadku
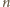 i
i
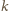 parzystych – a wiec
zawsze wygra.
parzystych – a wiec
zawsze wygra.
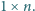 Na jej ostatnich
trzech polach stoi po jednym pionku. Dwóch graczy wykonuje naprzemiennie
ruchy polegające na przestawieniu dowolnego pionka na dowolne wolne pole
bliższe początku planszy. Przegrywa ten, który nie może zrobić ruchu.
Który z graczy ma strategię wygrywającą?
Na jej ostatnich
trzech polach stoi po jednym pionku. Dwóch graczy wykonuje naprzemiennie
ruchy polegające na przestawieniu dowolnego pionka na dowolne wolne pole
bliższe początku planszy. Przegrywa ten, który nie może zrobić ruchu.
Który z graczy ma strategię wygrywającą?

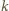 pionków stoi na końcowych polach planszy. Jeżeli zarówno
pionków stoi na końcowych polach planszy. Jeżeli zarówno
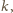 jak i
jak i
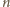 są parzyste, to dzieląc planszę na takie same szufladki
i przestawiając po każdym ruchu pierwszego gracza drugi pionek z szufladki,
w której stał pionek ruszony przez gracza pierwszego, do tej szufladki, do
której pierwszy gracz wstawił pionek, drugi gracz zapewni sobie zwycięstwo.
Jeżeli
są parzyste, to dzieląc planszę na takie same szufladki
i przestawiając po każdym ruchu pierwszego gracza drugi pionek z szufladki,
w której stał pionek ruszony przez gracza pierwszego, do tej szufladki, do
której pierwszy gracz wstawił pionek, drugi gracz zapewni sobie zwycięstwo.
Jeżeli
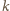 jest parzyste, a
jest parzyste, a
 nieparzyste – pierwszy gracz,
przestawiając ostatni pionek tuż przed pionek pierwszy, sprowadzi grę do
przypadku już rozważonego z sobą w roli drugiego, a więc wygra. Jeżeli
zaś
nieparzyste – pierwszy gracz,
przestawiając ostatni pionek tuż przed pionek pierwszy, sprowadzi grę do
przypadku już rozważonego z sobą w roli drugiego, a więc wygra. Jeżeli
zaś
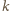 jest nieparzyste, to pierwszy gracz, przestawiając, w zależności
od parzystości
jest nieparzyste, to pierwszy gracz, przestawiając, w zależności
od parzystości
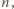 pierwszy bądź ostatni z pionków, zawsze może
sprowadzić grę do przypadku
pierwszy bądź ostatni z pionków, zawsze może
sprowadzić grę do przypadku
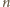 i
i
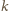 parzystych – a wiec
zawsze wygra.
parzystych – a wiec
zawsze wygra.