Zadanie ZM-1332
o zadaniu...
- Publikacja w Delcie: listopad 2011
- Publikacja elektroniczna: 01-11-2011

Bolek i Lolek grają w następujący wariant gry w czekoladę (por. artykuł
Wojciecha Czerwińskiego Zagrajmy w czekoladę): tabliczka ma wymiary
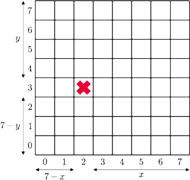
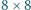 , jedna kostka jest zatruta (Rys. 2), w każdym ruchu gracz łamie
tabliczkę wzdłuż linii i zjada jedną z dwóch otrzymanych części. Przegrywa
ten, kto zje zatrutą kostkę. Grę rozpoczyna Bolek. Czy istnieje takie położenie
zatrutego pola, przy którym Bolek ma strategię wygrywającą?
, jedna kostka jest zatruta (Rys. 2), w każdym ruchu gracz łamie
tabliczkę wzdłuż linii i zjada jedną z dwóch otrzymanych części. Przegrywa
ten, kto zje zatrutą kostkę. Grę rozpoczyna Bolek. Czy istnieje takie położenie
zatrutego pola, przy którym Bolek ma strategię wygrywającą?

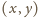 jest zatrute. Pokażemy, że Lolek ma
strategię wygrywającą. Gra polega tak naprawdę na zmniejszaniu przez graczy
w każdym ruchu jednej z liczb
jest zatrute. Pokażemy, że Lolek ma
strategię wygrywającą. Gra polega tak naprawdę na zmniejszaniu przez graczy
w każdym ruchu jednej z liczb
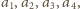 które na początku mają
wartości
które na początku mają
wartości
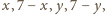 odpowiednio, a oznaczają liczbę kolumn na
prawo, na lewo, liczbę wierszy w górę, w dół od zatrutego pola w aktualnej
tabliczce czekolady. Rozważmy liczbę
odpowiednio, a oznaczają liczbę kolumn na
prawo, na lewo, liczbę wierszy w górę, w dół od zatrutego pola w aktualnej
tabliczce czekolady. Rozważmy liczbę
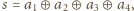 gdzie
gdzie
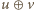 oznacza dodawanie liczb
oznacza dodawanie liczb
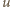 i
i
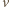 zapisanych binarnie,
bez przeniesienia (np.
zapisanych binarnie,
bez przeniesienia (np.
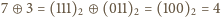 ).
).
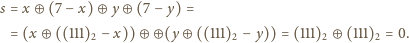
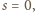 w następnym ruchu będziemy mieli
w następnym ruchu będziemy mieli
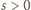 (któraś z liczb
(któraś z liczb
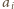 zmieniła się). Gdy
zmieniła się). Gdy
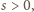 zawsze
istnieje taki ruch, że po jego wykonaniu
zawsze
istnieje taki ruch, że po jego wykonaniu
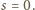 Istotnie, bez utraty
ogólności możemy zakładać, że
Istotnie, bez utraty
ogólności możemy zakładać, że
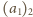 ma niezerowy bit na pozycji
pierwszego bitu znaczącego liczby
ma niezerowy bit na pozycji
pierwszego bitu znaczącego liczby
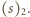 Wówczas
Wówczas
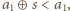 więc
wystarczy zmniejszyć liczbę
więc
wystarczy zmniejszyć liczbę
 o
o
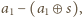 bo wtedy liczba
bo wtedy liczba
 wyniesie
wyniesie
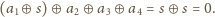
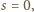 więc w końcu Bolek zastanie sytuację, w której
więc w końcu Bolek zastanie sytuację, w której
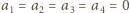 (w każdym ruchu któraś liczba się zmniejsza),
co odpowiada temu, że Bolek zostanie z zatrutą kostką i przegra.
(w każdym ruchu któraś liczba się zmniejsza),
co odpowiada temu, że Bolek zostanie z zatrutą kostką i przegra.