Zadanie ZM-1446
o zadaniu...
- Publikacja w Delcie: styczeń 2015
- Publikacja elektroniczna: 01-01-2015
Rozpatrzmy następującą grę. Przed rozpoczęciem dany jest stos z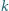 
monetami. Gracz wykonujący ruch musi usunąć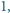 
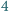lub 
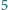monet ze stosu. Gracze wykonują ruchy na przemian. Jeśli któryś nie może wykonać ruchu, to przegrywa. Rozstrzygnąć, kto ma strategię wygrywającą, gdy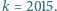 
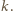Niech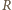 
oznacza gracza rozpoczynającego, zaś 
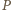jego przeciwnika.
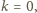gracz rozpoczynający 
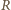nie może wykonać ruchu, więc wygrywa jego przeciwnik - gracz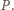 
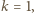to 
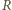zabiera 
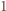monetę i 
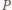dostaje pusty stos i przegrywa.
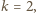to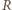 
musi zabrać 
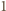monetę i przeciwnik jest w przed chwilą przeanalizowanej wygrywającej sytuacji.
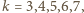to 
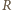zabiera odpowiednio 
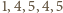monet, zostawiając przeciwnika z 
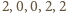monetami, czyli 
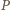jest w przed chwilą przeanalizowanych pozycjach przegrywających.
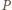wygrywa wtedy i tylko wtedy, gdy 
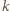przystaje modulo 8 do 0 lub 2. Skoro 
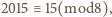to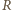 
ma strategię wygrywającą.