Zadanie ZM-1449
o zadaniu...
- Publikacja w Delcie: luty 2015
- Publikacja elektroniczna: 01-02-2015
Rozpatrzmy następującą grę. Przed rozpoczęciem gry dane są dwa niepuste stosy z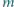 
i 
monetami. Ruch polega na usunięciu jednego ze stosów i podzieleniu drugiego na dwa niepuste. Gracze wykonują ruchy na przemian. Jeśli któryś nie może wykonać ruchu, to przegrywa. Rozstrzygnąć, kto ma strategię wygrywającą, gdy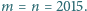 
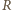oznacza gracza rozpoczynającego, zaś 
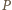jego przeciwnika. Wykażemy, że 
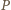ma strategię wygrywającą, polegającą na pozostawianiu po każdym swoim ruchu dwóch stosów o nieparzystej liczbie monet.
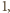to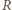 
po wykonaniu swojego ruchu zostawi dla 
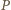stos z parzystą liczbą monet (i drugi o nieparzystej liczbie monet). Wówczas 
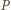może usunąć stos o nieparzystej liczbie monet, a ten o parzystej liczbie monet podzielić na dwa stosy zgodnie ze swoją strategią.
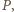gdy zostawi on dla 
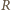dwa jednomonetowe stosy.