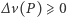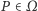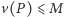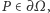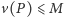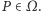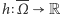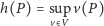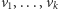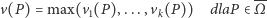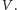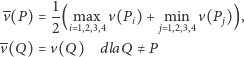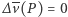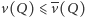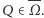Gra w sumo
Czy Czytelnik zna grę w przeciąganie liny? Dwie drużyny ciągną dwa końce liny w przeciwne strony, a wygrywa ta, której uda się przeciągnąć linę na swoją stronę. Ściślej, gra kończy się w momencie wyjścia środka liny (zazwyczaj oznaczonego wstążką) z umówionego pola gry. Matematycy przypisują tę samą nazwę podobnej grze rozgrywającej się w dwóch (i więcej) wymiarach, w której to środek liny może poruszać się w wielu kierunkach, a nie tylko lewo-prawo. Trudno sobie jednak takie przeciąganie wyobrazić, dlatego przyjąłem termin gra w sumo.

Plansza do gry w sumo (dalej oznaczana przez 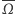 ) składa się z pewnej liczby pól na szachownicy. Każde pole szachownicy
) składa się z pewnej liczby pól na szachownicy. Każde pole szachownicy 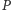 ma czterech sąsiadów, oznaczanych tutaj
ma czterech sąsiadów, oznaczanych tutaj 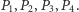 Pole nazwiemy wewnętrznym, jeśli leży na planszy razem ze swoimi sąsiadami, w przeciwnym przypadku nazwiemy je brzegowym. Zbiór pól wewnętrznych oznaczymy przez
Pole nazwiemy wewnętrznym, jeśli leży na planszy razem ze swoimi sąsiadami, w przeciwnym przypadku nazwiemy je brzegowym. Zbiór pól wewnętrznych oznaczymy przez 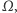 a brzegowych przez
a brzegowych przez 
Dwoje zawodników, Jaś i Małgosia, zaczyna grę na pewnym polu 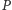 leżącym na planszy. Jeśli pole
leżącym na planszy. Jeśli pole 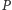 jest brzegowe, gra się kończy. W przeciwnym przypadku rzut symetryczną monetą decyduje, który z zawodników uzyskuje w tej turze przewagę nad przeciwnikiem, dzięki czemu przepycha go na wybrane przez siebie sąsiednie pole (i z rozpędu sam też tam ląduje). Gra toczy się w turach do momentu, gdy gracze wylądują na polu brzegowym.
jest brzegowe, gra się kończy. W przeciwnym przypadku rzut symetryczną monetą decyduje, który z zawodników uzyskuje w tej turze przewagę nad przeciwnikiem, dzięki czemu przepycha go na wybrane przez siebie sąsiednie pole (i z rozpędu sam też tam ląduje). Gra toczy się w turach do momentu, gdy gracze wylądują na polu brzegowym.
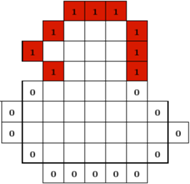
Rys. 1 Przykładowa plansza i funkcja rozstrzygnięcia. Jak widać, Małgosia postanowiła dać Jasiowi fory.
Kto wygrywa? Podobnie jak w grze w przeciąganie liny, musimy się na coś umówić. Dojście do pewnych pól brzegowych będzie oznaczać wygraną Jasia, a do innych - Małgosi. Przyjętą umowę możemy opisać za pomocą jednej funkcji 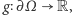 określonej wzorem
określonej wzorem

Przebieg gry jest więc zdeterminowany przez planszę 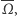 funkcję rozstrzygnięcia
funkcję rozstrzygnięcia 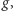 decyzje zawodników, losowe wyniki rzutów monetą oraz wybór pola startowego.
decyzje zawodników, losowe wyniki rzutów monetą oraz wybór pola startowego.
W dalszej części artykułu przyjmiemy, że Jaś i Małgosia mają ustalone racjonalne strategie, czyli przy każdym przepchnięciu przeciwnika wybierają sąsiednie pole w taki sposób, by zmaksymalizować prawdopodobieństwo swojej wygranej. Jeśli dodatkowo ustalimy pole startowe 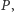 to gra jest już czysto losowa i możemy określić warunkowe prawdopodobieństwo wygranej Małgosi:
to gra jest już czysto losowa i możemy określić warunkowe prawdopodobieństwo wygranej Małgosi:

W ten sposób otrzymaliśmy pewną funkcję 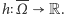 Gdy
Gdy 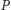 jest polem brzegowym, gra kończy się już na starcie, a jej rozstrzygnięcie jest opisane funkcją
jest polem brzegowym, gra kończy się już na starcie, a jej rozstrzygnięcie jest opisane funkcją 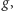 a zatem
a zatem 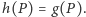 Rozgrywka robi się ciekawsza, jeśli
Rozgrywka robi się ciekawsza, jeśli 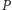 jest polem wewnętrznym. Z prawdopodobieństwem
jest polem wewnętrznym. Z prawdopodobieństwem 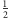 chwilową przewagę uzyska Małgosia i przepchnie Jasia na takie sąsiednie pole
chwilową przewagę uzyska Małgosia i przepchnie Jasia na takie sąsiednie pole 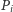 (gdzie
(gdzie 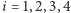 ), dla którego prawdopodobieństwo przyszłej wygranej
), dla którego prawdopodobieństwo przyszłej wygranej 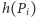 jest możliwie największe. Jeśli z kolei los padnie na Jasia, wybierze on takiego sąsiada
jest możliwie największe. Jeśli z kolei los padnie na Jasia, wybierze on takiego sąsiada 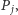 dla którego
dla którego 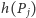 jest najmniejsze. Ze wzoru na prawdopodobieństwo całkowite otrzymujemy więc
jest najmniejsze. Ze wzoru na prawdopodobieństwo całkowite otrzymujemy więc

Dla dowolnej funkcji  różnicę obu stron powyższej równości oznaczymy przez
różnicę obu stron powyższej równości oznaczymy przez

Wyrażenie to jest nazywane dyskretnym operatorem 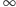 -Laplace'a (chociaż Pierre-Simon de Laplace (1749-1827) nigdy takiego nie rozważał). Dotychczasowe rozważania możemy podsumować następująco - funkcja
-Laplace'a (chociaż Pierre-Simon de Laplace (1749-1827) nigdy takiego nie rozważał). Dotychczasowe rozważania możemy podsumować następująco - funkcja  jest rozwiązaniem zagadnienia
jest rozwiązaniem zagadnienia
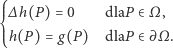 |
(*) |
Do znalezienia rozwiązania wykorzystamy metodę noszącą imię Oskara Perrona 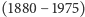 ; noszącą bardzo słusznie, gdyż to jemu ją zawdzięczamy. Opiera się ona na własnościach funkcji
; noszącą bardzo słusznie, gdyż to jemu ją zawdzięczamy. Opiera się ona na własnościach funkcji  spełniających nierówność
spełniających nierówność 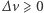 zamiast równości. Są to tak zwane podrozwiązania, których rodzinę oznaczymy przez
zamiast równości. Są to tak zwane podrozwiązania, których rodzinę oznaczymy przez

Rodzina 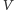 jest niepusta - należy do niej, na przykład, funkcja
jest niepusta - należy do niej, na przykład, funkcja  zerująca się na
zerująca się na 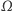 i równa funkcji
i równa funkcji 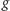 na
na 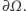 Ponadto wszystkie funkcje
Ponadto wszystkie funkcje  są ograniczone z góry przez
są ograniczone z góry przez 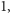 co wynika z następującego faktu:
co wynika z następującego faktu:
Wskazówka. Jeśli 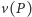 przyjmuje największą wartość dla pewnego pola
przyjmuje największą wartość dla pewnego pola 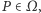 to przyjmuje tę samą wartość również dla wszystkich pól sąsiednich.
to przyjmuje tę samą wartość również dla wszystkich pól sąsiednich.
Jesteśmy teraz gotowi zdefiniować rozwiązanie.
Dotychczasowe uwagi na temat rodziny 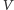 pozwalają stwierdzić, że powyższy wzór jest poprawny, a ponadto
pozwalają stwierdzić, że powyższy wzór jest poprawny, a ponadto 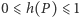 dla wszystkich
dla wszystkich  Narzuca się pytanie, czy znaleziona właśnie funkcja
Narzuca się pytanie, czy znaleziona właśnie funkcja 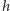 pokrywa się z rozważaną wcześniej funkcją opisującą prawdopodobieństwo wygranej. Poniższe zadanie rozwiewa tę wątpliwość.
pokrywa się z rozważaną wcześniej funkcją opisującą prawdopodobieństwo wygranej. Poniższe zadanie rozwiewa tę wątpliwość.
Zadanie 2 (o jednoznaczność). Zagadnienie (*) ma tylko jedno rozwiązanie.
Wskazówka. Rozważyć dwa rozwiązania 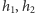 i powtórzyć rozumowanie z zadania 1 dla funkcji
i powtórzyć rozumowanie z zadania 1 dla funkcji 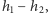 starannie dobierając punkt o ekstremalnych własnościach.
starannie dobierając punkt o ekstremalnych własnościach.
Dowód twierdzenia opiera się na dwóch wyjątkowych własnościach rodziny 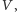 których samodzielne sprawdzenie nie powinno sprawić Czytelnikowi problemu.
których samodzielne sprawdzenie nie powinno sprawić Czytelnikowi problemu.
Dowód twierdzenia. Równość 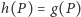 dla
dla 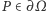 wynika wprost z określenia
wynika wprost z określenia 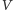 i
i 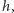 pozostaje nam sprawdzić równość
pozostaje nam sprawdzić równość  ; ustalmy więc pole
; ustalmy więc pole 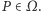 Z określenia
Z określenia 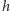 wynika, że dla każdej liczby
wynika, że dla każdej liczby  istnieje funkcja
istnieje funkcja 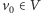 spełniająca
spełniająca 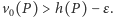 Podobnie dla każdego sąsiedniego pola
Podobnie dla każdego sąsiedniego pola 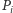 znajdziemy funkcję
znajdziemy funkcję 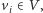 dla której
dla której 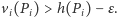 Ich wspólne ograniczenie
Ich wspólne ograniczenie 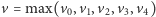 należy do rodziny
należy do rodziny 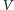 na mocy zadania 3 oraz
na mocy zadania 3 oraz

Skonstruowana w zadaniu 4 funkcja  również spełnia te nierówności, a ponadto dzięki
również spełnia te nierówności, a ponadto dzięki 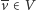 mamy
mamy 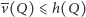 dla wszystkich
dla wszystkich 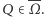 W rezultacie
W rezultacie

Porównanie liczb 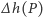 i
i 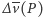 (ta druga jest zerem!) przy użyciu nierówności trójkąta daje
(ta druga jest zerem!) przy użyciu nierówności trójkąta daje

Powyższa nierówność jest prawdziwa dla dowolnie małej liczby 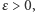 a więc zachodzi żądana równość
a więc zachodzi żądana równość 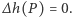
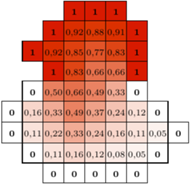
Rys. 2 Przybliżone rozwiązanie dla planszy i funkcji rozstrzygnięcia z rysunku 1
Zależnie od swojego filozoficznego usposobienia Czytelnik może być z tego dowodu zadowolony lub nie. Wykazaliśmy istnienie rozwiązania 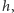 ale nie wyznaczyliśmy funkcji
ale nie wyznaczyliśmy funkcji 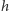 jawnym wzorem. Tę wadę ma zresztą większość metod stosowanych obecnie w równaniach różniczkowych cząstkowych, do których zagadnienie (*) zalicza się jako dyskretny odpowiednik.
jawnym wzorem. Tę wadę ma zresztą większość metod stosowanych obecnie w równaniach różniczkowych cząstkowych, do których zagadnienie (*) zalicza się jako dyskretny odpowiednik.
Problem ten można częściowo obejść. Funkcja 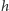 jest większa lub równa każdej funkcji
jest większa lub równa każdej funkcji 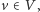 więc stosując na przemian konstrukcje z zadań 3 i 4, możemy znaleźć coraz lepsze przybliżenia z dołu. Gdybyśmy natomiast w definicji rodziny
więc stosując na przemian konstrukcje z zadań 3 i 4, możemy znaleźć coraz lepsze przybliżenia z dołu. Gdybyśmy natomiast w definicji rodziny 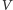 zastosowali przeciwny znak nierówności (czyli
zastosowali przeciwny znak nierówności (czyli 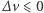 ), to funkcję
), to funkcję  otrzymalibyśmy jako infimum tej rodziny, co pozwala znaleźć przybliżenia
otrzymalibyśmy jako infimum tej rodziny, co pozwala znaleźć przybliżenia 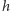 również z góry. W ten sposób możemy znaleźć wartości
również z góry. W ten sposób możemy znaleźć wartości 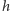 z dokładnością dwóch cyfr po przecinku dla planszy z rysunku 1 Warto zwrócić uwagę, że dopiero wtedy jesteśmy w stanie przeprowadzić symulacje naszej rozgrywki. O dziwo, w rzeczywistości zawodnicy sumo radzą sobie doskonale bez wykonywania takich obliczeń...
z dokładnością dwóch cyfr po przecinku dla planszy z rysunku 1 Warto zwrócić uwagę, że dopiero wtedy jesteśmy w stanie przeprowadzić symulacje naszej rozgrywki. O dziwo, w rzeczywistości zawodnicy sumo radzą sobie doskonale bez wykonywania takich obliczeń...