Bharati wyodrębnił szesnaście sutr i trzynaście powiązanych z nimi sutr zależnych (sub-sutr). Wedle dość swobodnej interpretacji świątobliwego męża opisują one algorytmy rozwiązywania problemów matematycznych: arytmetycznych, algebraicznych, geometrycznych i trygonometrycznych. Był to początek matematyki wedyjskiej w takiej postaci, w jakiej znamy ją dzisiaj. I choć co do wedyjskiego pochodzenia przedstawionych metod jest wiele poważnych wątpliwości, warto zwrócić uwagę na niektóre z tych rachunkowych skrótów.

Jednym z ciekawszych algorytmów jest sposób na podnoszenie do kwadratu za pomocą sutry Gunita Samuccayah, co po polsku oznacza: "produkt sumy". Dzięki tej formule możemy w kilka sekund podnosić bardzo duże liczby do kwadratu. Po odrobinie ćwiczeń powinno to zająć tyle czasu, ile zajmuje zapisanie wyniku. Jeśli chcemy korzystać z tej sutry, musimy najpierw poznać twór nazywany Duplexem. Możemy to przetłumaczyć (niekoniecznie najdokładniej) jako podwojenie. Dla liczb jednocyfrowych Duplex będzie ich kwadratem. Dla liczb dwucyfrowych Duplex tworzymy poprzez pomnożenie obydwu cyfr i podwojenie ich iloczynu. Tak więc dla liczby 34 będzie to: 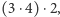co da nam 24; dla liczby 58: 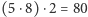itd. Dla liczb trzycyfrowych Duplex tworzymy, mnożąc pierwszą i ostatnią cyfrę, podwajając ten wynik i dodając do niego środkową cyfrę podniesioną do kwadratu. Tak więc dla liczby 634 tworzymy takie działanie: 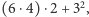co da nam 57; dla 452 będzie to: 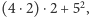co będzie równe 41 itd. W oparciu o powyższe przykłady możemy stworzyć coś na kształt ogólnej zasady, na podstawie której tworzymy Duplex. Bierzemy pierwszą i ostatnią cyfrę, mnożymy i podwajamy, następnie dodajemy do tego wynik mnożenia drugiej i przedostatniej cyfry, również podwojony 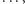a jeśli jakaś cyfra zostanie bez pary, podnosimy ją do kwadratu i dodajemy do pozostałych wyników. Teraz możemy przejść do właściwego podnoszenia do kwadratu. Jak Duplex nam w tym pomoże? Zacznijmy od prostych liczb: dwucyfrowych. Weźmy liczbę 23. Musimy pracować nad nią etapami. Pierwszy etap to wyliczenie Duplexu z 2, drugi to Duplex z 23 i ostatecznie z 3. Jeśli na jakimś etapie otrzymamy liczbę dwucyfrową, to cyfrę dziesiątek dodajemy do liczby znajdującej się po lewej stronie. Tak więc, oznaczając przez 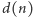Duplex liczby :

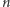Na razie, być może, nie wygląda na to, żeby ta metoda miała ułatwić obliczenia, poczekaj jednak, Czytelniku, na podnoszenie większych liczb do kwadratu. Z liczbami trzycyfrowymi postępujemy podobnie. Na początku obliczamy Duplex z pierwszej cyfry, następnie z pierwszych dwóch, kolejny etap to Duplex z całej liczby, potem z dwóch ostatnich cyfr i na koniec z ostatniej. W ten sposób:

Na podstawie tych przykładów możemy dostrzec ogólną zasadę. Bierzemy pierwszą cyfrę, następnie pierwsze dwie, pierwsze trzy, i kolejne, aż obliczymy Duplex z całej liczby. Następnie opuszczamy kolejno początkowe cyfry, aż dojdziemy do ostatniej. Dzięki Duplexowi możemy bardzo szybko podnosić liczby do kwadratu, jednak skąd możemy mieć pewność, że metoda ta zadziała w każdym przypadku? Jeśli nie mamy do dyspozycji kalkulatora, to podnosimy liczby do kwadratu za pomocą mnożenia pisemnego. Przyjrzyjmy się dokładniej podniesieniu do kwadratu w ten sposób liczby 23. Zacznijmy od końca. Widzimy, że ostatnia cyfra 9 tworzy się przez pomnożenie 3 i 3. Tak więc jest to 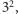czyli Duplex z 3. Następne są dwie szóstki, które po dodaniu dadzą nam 12. Jest to pomnożenie pierwszej i drugiej cyfry oraz ich podwojenie, czyli 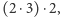co jest Duplexem z 23. Pierwszą cyfrą jest cztery, które jest wynikiem pomnożenia 2 i 2, czyli 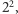co, jak wiemy, jest Duplexem z 2. Możemy przyjrzeć się podnoszeniu do kwadratu liczb wielocyfrowych, w każdym przypadku jest to analogia sposobu wedyjskiego.