Wieże Hanoi
Znana łamigłówka wieże Hanoi ma następujące reguły...
Na trzech słupkach (oznaczmy je literami 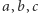 ) rozmieszczono
) rozmieszczono  krążków o różnych rozmiarach (ponumerujmy je od najmniejszego:
krążków o różnych rozmiarach (ponumerujmy je od najmniejszego: 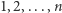 ) w taki sposób, by nigdy większy krążek nie leżał na mniejszym. W pojedynczym ruchu można przełożyć górny krążek z jednego słupka na górę innego, o ile jest on mniejszy od dotychczas leżących tam krążków. Oto przykładowe dozwolone ustawienie dla
) w taki sposób, by nigdy większy krążek nie leżał na mniejszym. W pojedynczym ruchu można przełożyć górny krążek z jednego słupka na górę innego, o ile jest on mniejszy od dotychczas leżących tam krążków. Oto przykładowe dozwolone ustawienie dla 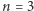 oraz ruchy możliwe do wykonania w tym momencie:
oraz ruchy możliwe do wykonania w tym momencie:
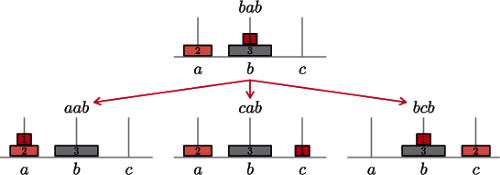
Każdy układ krążków na słupkach można opisać ciągiem o długości  złożonym z liter
złożonym z liter 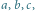 w którym kolejne znaki kodują położenie odpowiednich krążków. Zapis ten jest jednoznaczny, gdyż na każdym ze słupków krążki większe leżą pod mniejszymi.
w którym kolejne znaki kodują położenie odpowiednich krążków. Zapis ten jest jednoznaczny, gdyż na każdym ze słupków krążki większe leżą pod mniejszymi.
Klasycznym problemem związanym z wieżami Hanoi jest przełożenie wszystkich  krążków z jednego słupka na drugi w jak najmniejszej liczbie ruchów. Można zadać wiele innych pytań, na przykład o liczbę dozwolonych ustawień krążków, o liczbę wszystkich ruchów, o największą liczbę ruchów, w której można przełożyć
krążków z jednego słupka na drugi w jak najmniejszej liczbie ruchów. Można zadać wiele innych pytań, na przykład o liczbę dozwolonych ustawień krążków, o liczbę wszystkich ruchów, o największą liczbę ruchów, w której można przełożyć 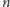 krążków z jednego słupka na drugi bez powtarzania żadnego ustawienia lub o to, czy przy najmniejszej liczbie ruchów pomiędzy dwoma ustawieniami największy krążek zawsze przekładany jest najwyżej raz.
krążków z jednego słupka na drugi bez powtarzania żadnego ustawienia lub o to, czy przy najmniejszej liczbie ruchów pomiędzy dwoma ustawieniami największy krążek zawsze przekładany jest najwyżej raz.
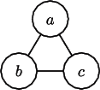
Rys. 1
Rys. 2
Nietrudno dostrzec, że na ogół możliwe do wykonania są dokładnie trzy ruchy, jak na powyższym schemacie: najmniejszy krążek zawsze można przenieść na dowolny z dwóch pozostałych słupków, ponadto z jednego z tych słupków na drugi można przenieść najmniejszy spośród leżących na nich krążków, chyba że oba są puste (czyli wszystkie krążki są na jednym słupku). Wtedy ten ostatni ruch nie jest możliwy i w tych i tylko tych sytuacjach można zrobić jedynie dwa różne ruchy.
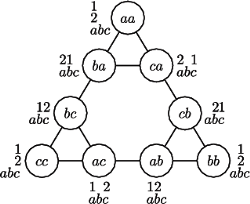
Zbudujmy graf ruchów dla wież Hanoi. Wierzchołkami grafu są wszystkie dozwolone ustawienia krążków, krawędziami zaś łączymy te wierzchołki, pomiędzy którymi można przejść w pojedynczym ruchu. Na mocy powyższej obserwacji w grafie tym są trzy wierzchołki (odpowiadające ustawieniom wszystkich krążków na jednym słupku), z których wychodzą po dwie krawędzie, a z każdego z pozostałych wierzchołków wychodzą dokładnie trzy krawędzie.
Rysunki 1-5 ilustrują grafy ruchów dla wież Hanoi kolejno dla
 (jeden krążek, przestawiany pomiędzy słupkami
(jeden krążek, przestawiany pomiędzy słupkami  ), dla
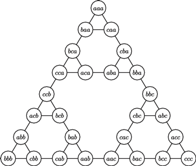
), dla  (obok każdego wierzchołka przedstawiono ustawienie, które mu odpowiada) oraz dla
(obok każdego wierzchołka przedstawiono ustawienie, które mu odpowiada) oraz dla  i
i 

Rys. 6
A oto kolejne kroki w konstrukcji trójkąta Sierpińskiego:
To zaskakujące podobieństwo oczywiście nie jest przypadkowe, ale jak je wyjaśnić? Zauważmy, że każdy z grafów na rysunkach 1-3 składa się z trzech części, odpowiadających ostatniej literze ciągu, czyli położeniu największego krążka (Rys. 7). Każda z takich części to graf ruchów dla 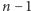 pozostałych krążków, a trzy krawędzie pomiędzy tymi częściami odpowiadają przełożeniu największego krążka na inny słupek.
pozostałych krążków, a trzy krawędzie pomiędzy tymi częściami odpowiadają przełożeniu największego krążka na inny słupek.
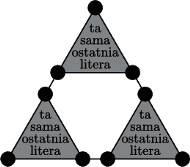
Rys. 7
Rysunek 7 przedstawia więc metodę konstrukcji grafów dla kolejnych  Ale to jest także metoda konstrukcji trójkąta Sierpińskiego z rysunku 6, co tłumaczy ich podobieństwo.
Ale to jest także metoda konstrukcji trójkąta Sierpińskiego z rysunku 6, co tłumaczy ich podobieństwo.
Analiza grafów ruchów dla wież Hanoi pozwala łatwo odpowiedzieć na pytania z początku artykułu. Pojedynczy ruch ilustrowany jest w grafie jako krawędź, więc ciąg ruchów to droga pomiędzy wierzchołkami. Stąd pytania o najmniejszą lub największą liczbę ruchów to pytania o najkrótszą lub najdłuższą drogę w grafie.
Rozwiązanie klasycznego problemu przestawienia wszystkich krążków z jednego słupka na drugi widać na grafie natychmiast: najkrótsza droga prowadzi wzdłuż odpowiedniego boku trójkąta. Ma ona długość 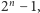 gdyż graf dla
gdyż graf dla 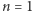 ma bok o długości
ma bok o długości 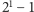 (Rys. 1), a długość boku każdego kolejnego grafu to dwukrotność długości poprzedniego boku zwiększona o 1 (Rys. 7).
(Rys. 1), a długość boku każdego kolejnego grafu to dwukrotność długości poprzedniego boku zwiększona o 1 (Rys. 7).
Z rysunku 7 (lub ze schematu z początku artykułu) wynika też natychmiast, że wierzchołków grafu (czyli dozwolonych ustawień krążków) jest 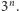 A ile jest wszystkich krawędzi grafu? To też można odczytać z rysunku 7.
A ile jest wszystkich krawędzi grafu? To też można odczytać z rysunku 7.
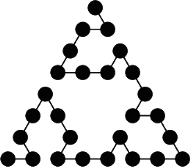
Rys. 8
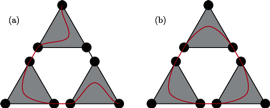
Rys. 9 Kolorowe łuki symbolizują najdłuższe drogi wewnątrz danych trójkątów (jak na Rys. 8).
Rysunek 8 ilustruje odpowiedź na pytanie o najdłuższą drogę dla 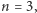 a na rysunku 9 (a) widzimy, jak na tej podstawie wyznaczyć analogiczną drogę dla większego
a na rysunku 9 (a) widzimy, jak na tej podstawie wyznaczyć analogiczną drogę dla większego 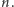 Można dostrzec, że jej długość to
Można dostrzec, że jej długość to 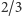 liczby wszystkich krawędzi grafu i - zarazem - liczba wszystkich wierzchołków zmniejszona o 1 (co pozwala inaczej niż powyżej wyznaczyć liczbę krawędzi grafu). W podobny sposób (Rys. 9 (b)) uzyskujemy drogę zamkniętą, przechodzącą przez każdy wierzchołek grafu dokładnie raz (tzw. cykl Hamiltona).
liczby wszystkich krawędzi grafu i - zarazem - liczba wszystkich wierzchołków zmniejszona o 1 (co pozwala inaczej niż powyżej wyznaczyć liczbę krawędzi grafu). W podobny sposób (Rys. 9 (b)) uzyskujemy drogę zamkniętą, przechodzącą przez każdy wierzchołek grafu dokładnie raz (tzw. cykl Hamiltona).
Powróćmy do pytania o najkrótszą drogę, ale niekoniecznie pomiędzy dwoma ustawieniami wszystkich krążków na jednym słupku. Załóżmy, że wierzchołki początkowy i końcowy są w różnych trójkątach grafu z rysunku 7 (jeśli są w tym samym, możemy rozważać tylko ten trójkąt, czyli graf dla mniejszego  ). Sprawa wydaje się prosta: wystarczy dojść od wierzchołka początkowego do krawędzi łączącej rozważane dwa trójkąty, przejść tą krawędzią do drugiego trójkąta i - już wewnątrz niego - dojść do wierzchołka końcowego.
). Sprawa wydaje się prosta: wystarczy dojść od wierzchołka początkowego do krawędzi łączącej rozważane dwa trójkąty, przejść tą krawędzią do drugiego trójkąta i - już wewnątrz niego - dojść do wierzchołka końcowego.
Rozumowanie to jest proste i 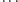 niepoprawne. Zgodnie z nim droga pomiędzy wierzchołkami
niepoprawne. Zgodnie z nim droga pomiędzy wierzchołkami 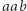 i
i 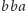 na rysunku 3 prowadzi najpierw do wierzchołka
na rysunku 3 prowadzi najpierw do wierzchołka 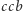 (3 ruchy), następnie krawędzią
(3 ruchy), następnie krawędzią  (1 ruch) i wreszcie do
(1 ruch) i wreszcie do 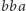 (kolejne 3 ruchy), ma więc długość 7. Tymczasem droga
(kolejne 3 ruchy), ma więc długość 7. Tymczasem droga 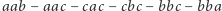 jest krótsza, a największy krążek przenoszony jest na niej dwukrotnie!
jest krótsza, a największy krążek przenoszony jest na niej dwukrotnie!
Co więcej, czasem istnieją dwie różne najkrótsze drogi, na przykład od 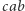 do
do 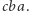 Pozostawiam Czytelnikom nietrudne już teraz poprawienie rozumowania oraz zachęcam do własnych badań nad wieżami Hanoi.
Pozostawiam Czytelnikom nietrudne już teraz poprawienie rozumowania oraz zachęcam do własnych badań nad wieżami Hanoi.
 złożonym z liter
złożonym z liter 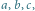 w którym kolejne znaki kodują położenie odpowiednich krążków. Zapis ten jest jednoznaczny, gdyż na każdym ze słupków krążki większe leżą pod mniejszymi.
w którym kolejne znaki kodują położenie odpowiednich krążków. Zapis ten jest jednoznaczny, gdyż na każdym ze słupków krążki większe leżą pod mniejszymi.