Naprawdę ciekawa gra
Mówi się, że gry (mniej lub bardziej) towarzyskie bywają interesujące i że wpływają pozytywnie na rozwój intelektualny gracza. To drugie jest całkowicie bezdyskusyjne i dodam optymistycznie, że rozwijać można się w każdym wieku. Moje duże wątpliwości budzi natomiast atrybut interesujące, który chyba zbyt pochopnie przypisuje się wielu grom. Osobiście nie potrafię zachwycić się przebiegiem rozgrywek nawet tak szacownych gier, jak szachy czy brydż, ale, jak wiadomo, o gustach się nie dyskutuje.
Jak to jest zrobione?
Cóż zatem ciekawego może być w grze towarzyskiej jako takiej? Według
mnie wyłącznie matematyka, która kryje się za jej zasadami (a niekoniecznie za
jej rozgrywką!). Oto dość świeży przykład takiej gry – żeby nie
uprawiać kryptoreklamy, nazwijmy ją roboczo grą
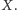 Talia składa się
z
Talia składa się
z
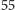 kart. Na każdej z nich jest
kart. Na każdej z nich jest
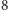 różnych obrazków typu:
słoneczko, kot, marchewka itp. … I teraz rzecz najważniejsza! Dowolne dwie
karty mają dokładnie jeden obrazek wspólny. W instrukcji zaproponowano
kilka prostych gier z użyciem takiej talii. Najprostsza polega na tym, że
dwóch graczy, z których każdy otrzymał początkowo
różnych obrazków typu:
słoneczko, kot, marchewka itp. … I teraz rzecz najważniejsza! Dowolne dwie
karty mają dokładnie jeden obrazek wspólny. W instrukcji zaproponowano
kilka prostych gier z użyciem takiej talii. Najprostsza polega na tym, że
dwóch graczy, z których każdy otrzymał początkowo
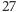 kart,
wykłada w każdym ruchu jedną kartę na stół (jedna karta nie bierze
udziału w grze). Ten, który jako pierwszy spostrzeże i nazwie wspólny
obrazek, wygrywa ruch i pozbywa się tej karty. Wygrywa ten, który
wcześniej pozbędzie się wszystkich kart. W przypadku większej liczby graczy
możliwe są dość oczywiste warianty, które czynią grę jeszcze ciekawszą
(?).
kart,
wykłada w każdym ruchu jedną kartę na stół (jedna karta nie bierze
udziału w grze). Ten, który jako pierwszy spostrzeże i nazwie wspólny
obrazek, wygrywa ruch i pozbywa się tej karty. Wygrywa ten, który
wcześniej pozbędzie się wszystkich kart. W przypadku większej liczby graczy
możliwe są dość oczywiste warianty, które czynią grę jeszcze ciekawszą
(?).
Ale my nie chcemy tutaj zajmować się rozgrywką, lecz zadajemy pytanie
podstawowe: jak zaprojektować karty, aby spełniony był warunek, że każde
dwie mają dokładnie jeden wspólny obrazek? O tym traktuje ten artykuł.
Uważny Czytelnik od razu zauważy, że na tak sformułowane pytanie
odpowiedź jest trywialna: na każdej z
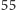 kart należy umieścić
słoneczko, a pozostałe
kart należy umieścić
słoneczko, a pozostałe
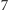 miejsc obsadzić
miejsc obsadzić
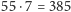 różnymi
przedmiotami! Jednak chodzi nam o coś więcej: pobieżna inspekcja talii kart
przekonuje nas, że różnych obrazków jest około
różnymi
przedmiotami! Jednak chodzi nam o coś więcej: pobieżna inspekcja talii kart
przekonuje nas, że różnych obrazków jest około
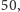 a nie ponad
a nie ponad
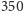 ! Po dłuższej grze zauważamy ponadto, że wspólne obrazki
z całego katalogu obrazków pojawiają się mniej więcej równomiernie (np.
słoneczko podobnie często jak marchewka!). To wszystko rozgrywało się na polu
namiotowym w Polańczyku, nad pięknym Jeziorem Solińskim. Moich
kompanów wypoczynku (wyłącznie niematematyków!) zachwyciło właśnie
to: bezkompromisowe przestrzeganie reguły w nietrywialny sposób!
Zapytali mnie wprost: Jak to jest zrobione? Poszli pływać na deskach,
a ja znowu miałem pretekst, żeby zostać w bazie windsurfingowej
Malibu.
! Po dłuższej grze zauważamy ponadto, że wspólne obrazki
z całego katalogu obrazków pojawiają się mniej więcej równomiernie (np.
słoneczko podobnie często jak marchewka!). To wszystko rozgrywało się na polu
namiotowym w Polańczyku, nad pięknym Jeziorem Solińskim. Moich
kompanów wypoczynku (wyłącznie niematematyków!) zachwyciło właśnie
to: bezkompromisowe przestrzeganie reguły w nietrywialny sposób!
Zapytali mnie wprost: Jak to jest zrobione? Poszli pływać na deskach,
a ja znowu miałem pretekst, żeby zostać w bazie windsurfingowej
Malibu.
Szukałem podobnych sytuacji w różnych działach matematyki i dość szybko ustaliłem, że „dwie różne proste przecinają się na ogół w dokładnie jednym punkcie”. U nas „proste” będą kartami, a „punkty” będą obrazkami. Odważnie brnąłem dalej, ufając klasykom, którzy w roli „punktów” widzieli nawet krzesła, byle spełniały aksjomaty! Póki co przeszkadzało mi bardzo wytłuszczone zastrzeżenie na ogół, które dopuszcza, że są na świecie proste równoległe. Ale my nie chcemy dopuszczać żadnych wyjątków! Każde dwie różne „proste” powinny przecinać się w dokładnie jednym „punkcie”. Czy są takie dziwne geometrie? Są i to pod ręką!
Czytelnik Delty słyszał zapewne o płaszczyźnie rzutowej, ale dla
porządku przypomnijmy jej konstrukcję. Niech
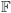 będzie
dowolnym ciałem. Oznaczmy najpierw zbiór trójek elementów
będzie
dowolnym ciałem. Oznaczmy najpierw zbiór trójek elementów
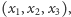 gdzie
gdzie
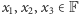 przez
przez
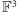 i wprowadźmy
w
i wprowadźmy
w
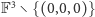 następującą relację
następującą relację
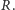 Piszemy
Piszemy
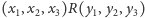 wówczas, gdy istnieje
wówczas, gdy istnieje
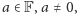 takie,
że
takie,
że
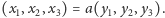 Łatwo sprawdzić, że
Łatwo sprawdzić, że
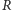 jest relacją
równoważności na zbiorze
jest relacją
równoważności na zbiorze
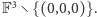 Określamy teraz
płaszczyznę rzutową nad ciałem
Określamy teraz
płaszczyznę rzutową nad ciałem
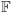 jako zbiór
jako zbiór
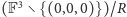 klas abstrakcji relacji
klas abstrakcji relacji
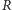 i oznaczamy go tradycyjnie symbolem
i oznaczamy go tradycyjnie symbolem
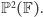
Jeśli, na przykład,
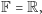 to możemy rozpatrywać punkt
to możemy rozpatrywać punkt
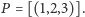 Biorąc
Biorąc
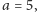 możemy ten sam punkt
możemy ten sam punkt
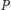 zapisać inaczej:
zapisać inaczej:
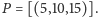 Określmy jeszcze proste
w naszej geometrii. Jeśli
Określmy jeszcze proste
w naszej geometrii. Jeśli
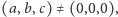 to określamy prostą
to określamy prostą
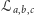 jako zbiór punktów
jako zbiór punktów
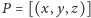 spełniających
równanie
spełniających
równanie

Proszę zauważyć, że tak określona przynależność punktu
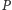 do
prostej nie zależy od wyboru przedstawiciela
do
prostej nie zależy od wyboru przedstawiciela
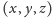 z klasy
abstrakcji. Jeśli rozpatrzymy teraz dwie różne proste
z klasy
abstrakcji. Jeśli rozpatrzymy teraz dwie różne proste
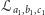 oraz
oraz
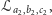 co oznacza, że nie istnieje
co oznacza, że nie istnieje
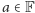 takie, iż
takie, iż
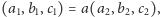 to wówczas będzie
to wówczas będzie

Natychmiast sprawdzamy bezpośrednim rachunkiem, że

Mamy więc to, czego chcieliśmy: każde dwie różne proste przecinają
się w jednym punkcie (i tylko w jednym, co łatwo sprawdzić)! Do
rozwiązania pozostał jeszcze jeden problem: na prostej w
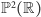 jest
nieskończenie wiele punktów, a na karcie gry
jest
nieskończenie wiele punktów, a na karcie gry
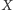 ma być
zaledwie
ma być
zaledwie
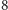 obrazków. Ale dla matematyka to żaden problem:
ciało
obrazków. Ale dla matematyka to żaden problem:
ciało
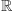 jest po prostu zbyt duże, zamiast
jest po prostu zbyt duże, zamiast
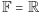 należy
użyć ciała skończonego
należy
użyć ciała skończonego
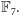 Składa się ono z wszystkich reszt
modulo
Składa się ono z wszystkich reszt
modulo
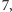 a zatem
a zatem
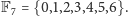 Działania też są
określone modulo
Działania też są
określone modulo
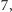 np.:
np.:
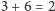 ;
;
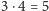 ;
;
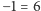 ;
;
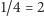 itp. Przekonajmy się, że na każdej prostej
itp. Przekonajmy się, że na każdej prostej
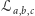 leży
dokładnie
leży
dokładnie
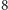 punktów. Załóżmy, że np.
punktów. Załóżmy, że np.
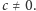 Z równania
prostej obliczamy
Z równania
prostej obliczamy
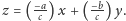 Mamy teraz ogromną swobodę. Za
Mamy teraz ogromną swobodę. Za
 i
i
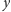 możemy podstawiać niezależnie wszystkie elementy
ciała
możemy podstawiać niezależnie wszystkie elementy
ciała
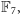 omijając tylko parę
omijając tylko parę
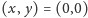 (dlaczego?).
Razem z wynikowym
(dlaczego?).
Razem z wynikowym
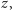 obliczonym z powyższego wzoru,
otrzymamy wówczas
obliczonym z powyższego wzoru,
otrzymamy wówczas
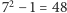 trójek, których klasy abstrakcji
wyczerpują całą prostą – każdy punkt na prostej otrzymamy jednak
sześciokrotnie, a zatem
trójek, których klasy abstrakcji
wyczerpują całą prostą – każdy punkt na prostej otrzymamy jednak
sześciokrotnie, a zatem
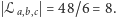 Podobnie obliczamy, że
Podobnie obliczamy, że
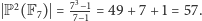 A ile jest prostych w naszej geometrii?
Z powyższego opisu wynika, że również
A ile jest prostych w naszej geometrii?
Z powyższego opisu wynika, że również
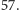 Każdy bowiem punkt
Każdy bowiem punkt
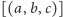 wyznacza prostą
wyznacza prostą
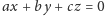 i odwrotnie –
zjawisko to nazywamy dualnością i odgrywa ono ważną rolę w geometrii
rzutowej. Coś tu się jednak nie zgadza, gdyż talia składa się z
i odwrotnie –
zjawisko to nazywamy dualnością i odgrywa ono ważną rolę w geometrii
rzutowej. Coś tu się jednak nie zgadza, gdyż talia składa się z
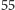 kart –
no dobrze, nie użyto po prostu pewnych dwóch prostych – zapewne
z powodów eko-logicznych. Może przynajmniej zgadza się liczba różnych
obrazków (czyli punktów) użytych przez projektanta gry
kart –
no dobrze, nie użyto po prostu pewnych dwóch prostych – zapewne
z powodów eko-logicznych. Może przynajmniej zgadza się liczba różnych
obrazków (czyli punktów) użytych przez projektanta gry
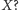
Zniknęli za horyzontem i szybko nie wrócą ..., a więc do roboty: „kotek,
marchewka, słoneczko … znowu słoneczko – już było, więc nie liczymy
powtórnie ... diabełek.” „Jeden, dwa, trzy, ..., pięćdziesiąt siedem.”–
dzięki Ci Boże za te piękne wzgórza, jezioro i płaszczyznę rzutową
 !
!
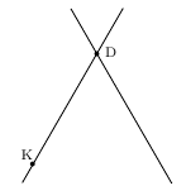
Rys. 1 Brakujące proste
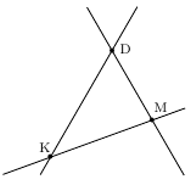
Rys. 2 Prosta KM jest w talii
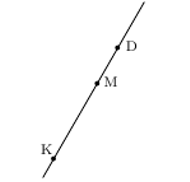
Rys. 3 M leży na prostej DK.
Brakujące karty
Jeśli gra
 jest rozrywkowym wcieleniem absolutu
jest rozrywkowym wcieleniem absolutu
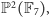 to
medytacjom z użyciem talii kart przeszkadza niewątpliwie jej niezupełność –
brak dwóch kart. Matematyk nie może przejść nad tym do porządku
dziennego – już woli nawet nie grać, niż przestać myśleć o dwóch
brakujących kartach. Już słyszę te złośliwości pod naszym adresem:
„Lubujecie się w rozmyślaniach nad tym, czego nie ma”. Na szczęście
pogłębiona opinia o działalności matematyków zawiera stwierdzenie: „Oni
rachują”. A więc do roboty!
to
medytacjom z użyciem talii kart przeszkadza niewątpliwie jej niezupełność –
brak dwóch kart. Matematyk nie może przejść nad tym do porządku
dziennego – już woli nawet nie grać, niż przestać myśleć o dwóch
brakujących kartach. Już słyszę te złośliwości pod naszym adresem:
„Lubujecie się w rozmyślaniach nad tym, czego nie ma”. Na szczęście
pogłębiona opinia o działalności matematyków zawiera stwierdzenie: „Oni
rachują”. A więc do roboty!
Policzę najpierw, na ilu kartach występuje słoneczko: wyszło, że na 8. Tak więc
cały pęk prostych przechodzących przez słoneczko jest nienaruszony. Podobnie
piesek występuje na 8 kartach, ale gorszy los spotkał kotka K – podobnie jak 13
innych przedmiotów występuje na
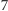 kartach. Diabełek D jest
niepocieszony, chociaż wyróżniony: tylko on występuje na 6 kartach.
Rysunek 1 ilustruje powyższy opis werbalny. „Prosta” DK (przechodząca przez
diabełka i kotka) jest, oczywiście, jedną z brakujących prostych. Rozważmy
teraz jeden z 13 pozostałych przedmiotów, oprócz K, leżących na 7 prostych
– niech to będzie marchewka M. Mamy rozstrzygnąć problem: czy M leży na
prostej DK, czy też na drugiej brakującej?
kartach. Diabełek D jest
niepocieszony, chociaż wyróżniony: tylko on występuje na 6 kartach.
Rysunek 1 ilustruje powyższy opis werbalny. „Prosta” DK (przechodząca przez
diabełka i kotka) jest, oczywiście, jedną z brakujących prostych. Rozważmy
teraz jeden z 13 pozostałych przedmiotów, oprócz K, leżących na 7 prostych
– niech to będzie marchewka M. Mamy rozstrzygnąć problem: czy M leży na
prostej DK, czy też na drugiej brakującej?
W tym celu należy wyjąć z tali wszystkie 7 kart „przechodzących” przez
kotka K. Jeśli jest wśród nich karta zawierająca marchewkę M, to M leży na
drugiej brakującej prostej. Jeśli natomiast żadna z tych kart nie przechodzi
przez M, to M leży na prostej DK; inaczej mówiąc, diabełek, kotek
i marchewka są współliniowe! Obie te sytuacje przedstawiono odpowiednio na
rysunkach 2 i 3. Tak samo sadowimy pozostałe przedmioty leżące na
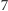 prostych.
prostych.
Proszę zauważyć, że rozwiązanie problemu brakujących prostych nie
wymagało użycia współrzędnych, tzn. nie pracowaliśmy z równaniami
w
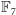 jak w poprzedniej części artykułu. Korzystaliśmy wyłącznie
z własności „geometrycznych” typu: każda prosta zawiera 8 punktów,
każdy punkt leży na 8 prostych itp. Te własności i wiele innych można
wywieść z następujących aksjomatów abstrakcyjnej planimetrii rzutowej:
jak w poprzedniej części artykułu. Korzystaliśmy wyłącznie
z własności „geometrycznych” typu: każda prosta zawiera 8 punktów,
każdy punkt leży na 8 prostych itp. Te własności i wiele innych można
wywieść z następujących aksjomatów abstrakcyjnej planimetrii rzutowej:
- A1
- Przez każde dwa różne punkty przechodzi dokładnie jedna prosta.
- A2
- Każde dwie różne proste przechodzą przez dokładnie jeden wspólny punkt.
- A3
- Istnieją cztery różne punkty, z których żadne trzy nie leżą na jednej prostej.
Wychodząc z tych aksjomatów, można, na przykład, wykazać, że jeśli cała
płaszczyzna składa się ze skończonej liczby punktów, to ta skończona liczba
musi być postaci
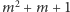 oraz
oraz
- na każdej prostej leży
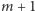 punktów,
punktów,
- przez każdy punkt przechodzi
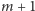 prostych,
prostych,
- wszystkich prostych jest też
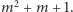
Liczbę
 nazywamy rzędem skończonej płaszczyzny rzutowej. Płaszczyzna
nazywamy rzędem skończonej płaszczyzny rzutowej. Płaszczyzna
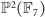 ma rząd
ma rząd
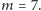 Jakie liczby naturalne
Jakie liczby naturalne
 są rzędami
skończonych płaszczyzn rzutowych? Jeżeli
są rzędami
skończonych płaszczyzn rzutowych? Jeżeli
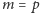 jest liczbą
pierwszą, to uogólniając przedstawioną wyżej konstrukcję (używając ciała
reszt
jest liczbą
pierwszą, to uogólniając przedstawioną wyżej konstrukcję (używając ciała
reszt
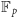 zamiast szczególnego ciała reszt
zamiast szczególnego ciała reszt
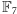 ), otrzymujemy
płaszczyznę rzutową rzędu
), otrzymujemy
płaszczyznę rzutową rzędu
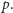 Tego typu konstrukcja wychodzi z ciała
Tego typu konstrukcja wychodzi z ciała
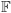 i produkuje płaszczyznę
i produkuje płaszczyznę
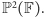 Okazuje się, że
Okazuje się, że
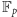 nie
są jedynymi ciałami skończonymi. Pełny opis sytuacji zawiera się w klasycznym
twierdzeniu, że dla każdej liczby pierwszej
nie
są jedynymi ciałami skończonymi. Pełny opis sytuacji zawiera się w klasycznym
twierdzeniu, że dla każdej liczby pierwszej
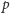 i każdej liczby naturalnej
i każdej liczby naturalnej
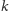 istnieje dokładnie jedno ciało o liczbie elementów
istnieje dokładnie jedno ciało o liczbie elementów
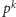 ;
oznaczamy je przez
;
oznaczamy je przez
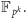 Zobaczmy dla przykładu, jak powstaje ciało
Zobaczmy dla przykładu, jak powstaje ciało
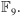 Niech
Niech
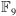 jako zbiór składa się z napisów postaci
jako zbiór składa się z napisów postaci
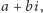 gdzie
gdzie
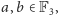 natomiast
natomiast
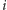 jest osobnym
przedmiotem. Określmy działania w
jest osobnym
przedmiotem. Określmy działania w
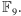 Dodawanie i odejmowanie
wykonujemy „po współrzędnych”:
Dodawanie i odejmowanie
wykonujemy „po współrzędnych”:

I tak, na przykład,

i tak dalej.
Mnożenie
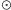 jest ciekawsze (chociaż nie dla Czytelnika, który zna
liczby zespolone):
jest ciekawsze (chociaż nie dla Czytelnika, który zna
liczby zespolone):

Można sprawdzić, że otrzymujemy w ten sposób ciało, tzn. spełnione są
wszystkie naturalne własności dodawania, odejmowania, mnożenia i dzielenia
znane z arytmetyki liczb rzeczywistych. Czytelnik może się zastanowić, jak
znajdować elementy odwrotne do elementów różnych od
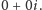 My
zadowolimy się przykładem dzielenia:
My
zadowolimy się przykładem dzielenia:

Tak więc
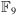 składa się z
składa się z
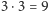 elementów i jest ciałem – mamy
więc płaszczyznę rzutową rzędu 9 i możemy zaprojektować odpowiednią grę
z
elementów i jest ciałem – mamy
więc płaszczyznę rzutową rzędu 9 i możemy zaprojektować odpowiednią grę
z
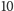 obrazkami na każdej z (nawet)
obrazkami na każdej z (nawet)
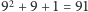 kart. Grę
„minimalną” otrzymamy, wychodząc z płaszczyzny rzutowej
kart. Grę
„minimalną” otrzymamy, wychodząc z płaszczyzny rzutowej
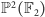 –
karty są trzyobrazkowe i jest ich
–
karty są trzyobrazkowe i jest ich
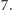 Słynna hipoteza mówi, że jedynie
potęgi liczb pierwszych
Słynna hipoteza mówi, że jedynie
potęgi liczb pierwszych
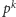 są rzędami skończonych płaszczyzn
rzutowych.
są rzędami skończonych płaszczyzn
rzutowych.
Póki co najogólniejsze twierdzenie w tym kierunku udowodnili Bruck i Ryser (1949):
Twierdzenie. Jeśli istnieje płaszczyzna rzutowa rzędu
 oraz
oraz
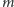 daje resztę 1 lub 2 w dzieleniu przez 4, to
daje resztę 1 lub 2 w dzieleniu przez 4, to
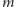 jest sumą
kwadratów dwóch liczb całkowitych.
jest sumą
kwadratów dwóch liczb całkowitych.
Wynika z tego natychmiast, że
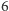 nie jest rzędem płaszczyzny
rzutowej – gry
nie jest rzędem płaszczyzny
rzutowej – gry
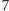 -obrazkowej nie da się skonstruować. Pierwsza liczba
-obrazkowej nie da się skonstruować. Pierwsza liczba
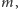 która nie podpada pod powyższe twierdzenie, to
która nie podpada pod powyższe twierdzenie, to
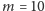 –
używając dobrych pomysłów i bardzo mocnych komputerów (Lam, Thiel,
Swiercz, 1989), wykazano, że nie ma płaszczyzny rzutowej rzędu
–
używając dobrych pomysłów i bardzo mocnych komputerów (Lam, Thiel,
Swiercz, 1989), wykazano, że nie ma płaszczyzny rzutowej rzędu
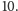 Nie
wiadomo, czy istnieje płaszczyzna rzutowa rzędu
Nie
wiadomo, czy istnieje płaszczyzna rzutowa rzędu
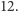
Wróćmy wreszcie do oryginalnej gry
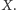 Zauważmy przede wszystkim,
że jej projektanci nie musieli a priori korzystać z całej tej algebraicznej
konstrukcji, która wychodzi od ciała
Zauważmy przede wszystkim,
że jej projektanci nie musieli a priori korzystać z całej tej algebraicznej
konstrukcji, która wychodzi od ciała
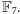 Może zrobili to „na
piechotę” i mieli bardzo dużo szczęścia? To oczywiście możliwe,
bo, jak wiadomo, szczęścia nigdy za dużo, ale można udowodnić,
że płaszczyzny rzutowe rzędów
Może zrobili to „na
piechotę” i mieli bardzo dużo szczęścia? To oczywiście możliwe,
bo, jak wiadomo, szczęścia nigdy za dużo, ale można udowodnić,
że płaszczyzny rzutowe rzędów
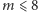 muszą pochodzić od
ciał skończonych – tak więc nawet jeśli twórcy gry nie korzystali ze
współrzędnych w ciele
muszą pochodzić od
ciał skończonych – tak więc nawet jeśli twórcy gry nie korzystali ze
współrzędnych w ciele
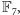 to faktycznie te współrzędne daje się
wprowadzić i może być np. tak, że
to faktycznie te współrzędne daje się
wprowadzić i może być np. tak, że
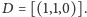 Natomiast oprócz
dość dokładnie opisanej powyżej płaszczyzny
Natomiast oprócz
dość dokładnie opisanej powyżej płaszczyzny
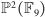 istnieją
jeszcze trzy inne płaszczyzny rzutowe rzędu
istnieją
jeszcze trzy inne płaszczyzny rzutowe rzędu
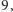 w których nie da
się wprowadzić współrzędnych z ciała
w których nie da
się wprowadzić współrzędnych z ciała
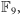 a nawet więcej: nie
zachodzi w nich twierdzenie Desarguesa, ale to już historia na inną
opowieść.
a nawet więcej: nie
zachodzi w nich twierdzenie Desarguesa, ale to już historia na inną
opowieść.
Na zakończenie przepis na zrobienie sobie talii kart opartej na
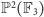
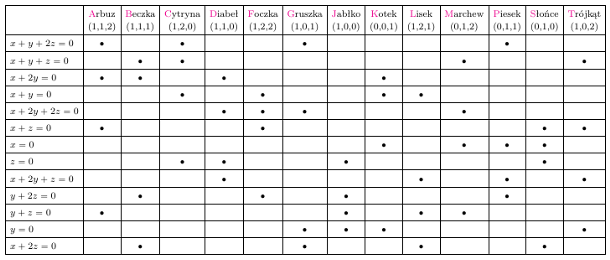
Talia pomniejszona, ale kompletna: Arbuz ma współrzędne jednorodne
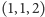 oraz leży na prostych pierwszej, trzeciej, szóstej i jedenastej,
gdyż liczby
oraz leży na prostych pierwszej, trzeciej, szóstej i jedenastej,
gdyż liczby
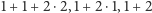 dzielą się przez 3. Zarówno
prostych, jak i punktów jest
dzielą się przez 3. Zarówno
prostych, jak i punktów jest
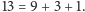 Na każdej prostej leżą
Na każdej prostej leżą
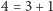 punkty, przez każdy z 13 punktów przechodzą 4 proste
i wreszcie każde dwie różne proste mają dokładnie jeden punkt wspólny –
proszę sprawdzić! Oczywiście, możliwych czwórek obrazków jest dużo
więcej (55 razy, ale to „inne” 55) niż tych, które będą na jednej karcie-prostej:
już Arbuz, Beczka i Cytryna nie znajdują się równocześnie na żadnej
karcie.
punkty, przez każdy z 13 punktów przechodzą 4 proste
i wreszcie każde dwie różne proste mają dokładnie jeden punkt wspólny –
proszę sprawdzić! Oczywiście, możliwych czwórek obrazków jest dużo
więcej (55 razy, ale to „inne” 55) niż tych, które będą na jednej karcie-prostej:
już Arbuz, Beczka i Cytryna nie znajdują się równocześnie na żadnej
karcie.