Rys. 1 Przykładowa rozgrywka. Ramka na górze zawiera ukryty kod; poniżej znajdują się kolejne pytania (zgadnięcia) oraz uzyskiwane odpowiedzi: czarna szpilka oznacza trafienie celne, biała – niecelne. Gracz odgadujący wygrywa, gdy otrzyma odpowiedź ,,cztery kropki” w określonej liczbie ruchów. (My przyjmiemy, że wystarczy mu pewność, że otrzyma ją za chwilę.)

W można grać, gimnastykując pomysłowość na bieżąco – ale matematyk chciałby też poszukać ogólnej metody. Jaka jest najmniejsza liczba pytań, która zawsze wystarczy do zwycięstwa? To niełatwy problem, ale możemy wspomóc się komputerem: właśnie w ten sposób Donald Knuth uzyskał w 1977 roku wynik czterech pytań. Komputery nie radzą sobie jednak z uogólnioną wersją gry, gdy kod zawiera 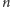 szpilek (zamiast 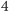), a do dyspozycji jest 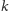 kolorów (zamiast 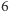). Nie zdziwi nas to, gdy pomyślimy, jakich rachunków wymaga uzasadnienie, że do zwycięstwa potrzeba przynajmniej 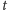 ruchów. Teoretycznie należy przejrzeć drzewo stanów gry (możliwych ciągów pytań i odpowiedzi) do głębokości 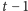 ruchów włącznie. Dla gry standardowej oraz 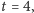 jako że możliwych pytań w grze jest 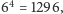 zaś odpowiedzi 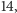 samych stanów na głębokości 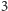 mamy 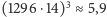 biliona! Na szczęście możemy zauważyć, że stany różniące się jedynie przemianowaniem kolorów i/lub pozycji są właściwie równoważne – jeśli przejrzeliśmy możliwości wygrania w jednym z nich, nie trzeba już zajmować się tym drugim. Zmniejsza to liczbę istotnych stanów do około 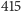 milionów (tj. ponad 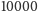-krotnie!), co – w połączeniu z pewnymi dodatkowymi usprawnieniami – czyni zadanie dostępnym dla domowego komputera. Zauważmy jednak, że w ogólności nasz problem wciąż zachowuje się wykładniczo względem 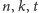: powiększając te parametry choćby o 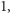  możemy zwiększyć trudność setki razy. Nic więc dziwnego, że nawet dla 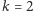 udało się dotychczas (z wykorzystaniem dużo bardziej złożonych technik) znaleźć optymalne strategie jedynie dla

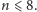
Skoro nie umiemy znaleźć najlepszej strategii dla gry z 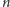  szpilkami w 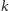  kolorach, poszukajmy (bez komputera) możliwie dobrej. Na początek załóżmy, że 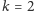: szpilki są jedynie ciemnoszarei kolorowe. Łatwo wówczas wygrać, zadając 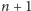 pytań: w pierwszym wszystkie szpilki są ciemnoszare, w następnych jedna kolorowaszpilka „wędruje” po kolejnych pozycjach. (Właściwie ostatnie z tych pytań jest zbędne, zatem można wygrać w 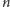  ruchach.) A czy da się lepiej?

Pełna treść artykułu dostępna jest w wersji do druku.