Mała Delta
Numizmatyka dla zachłannych
Wyobraźmy sobie następującą grę. Na stole w jednym rzędzie leży
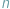 monet o różnych nominałach. Dwoje graczy – Ania i Bartek –
wykonuje na przemian ruchy, zaczyna Ania. Ruch polega na zabraniu jednej
monety z lewego lub prawego końca rzędu. Wynikiem gry jest, oczywiście,
suma nominałów monet zgromadzonych przez każdego z graczy. Jak powinna
grać Ania, by uzyskać jak największą sumę, jeśli wie ona, że Bartek
będzie grał optymalnie (tzn. będzie starał się zmaksymalizować swoją
sumę)?
monet o różnych nominałach. Dwoje graczy – Ania i Bartek –
wykonuje na przemian ruchy, zaczyna Ania. Ruch polega na zabraniu jednej
monety z lewego lub prawego końca rzędu. Wynikiem gry jest, oczywiście,
suma nominałów monet zgromadzonych przez każdego z graczy. Jak powinna
grać Ania, by uzyskać jak największą sumę, jeśli wie ona, że Bartek
będzie grał optymalnie (tzn. będzie starał się zmaksymalizować swoją
sumę)?
Na rozgrzewkę rozważmy prosty przykład dla
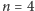 :
:
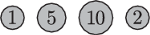
Spróbujmy zastosować strategię zachłanną, polegającą na tym, że w każdym ruchu wybieramy ten kraniec, na którym znajduje się moneta o większym nominale. Zatem w pierwszym ruchu Ania weźmie 2:

Optymalnym ruchem Bartka w takiej sytuacji jest wzięcie 10. Po czym Ania
weźmie 5, a Bartek 1. W takiej sytuacji przewaga Ani nad Bartkiem wyniosła
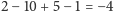 (przez przewagę rozumiemy tu sumę nominałów
zgromadzonych przez jednego z graczy pomniejszoną o sumę nominałów
przeciwnika – nie przeszkadza nam to, że czasem ta przewaga będzie
ujemna).
(przez przewagę rozumiemy tu sumę nominałów
zgromadzonych przez jednego z graczy pomniejszoną o sumę nominałów
przeciwnika – nie przeszkadza nam to, że czasem ta przewaga będzie
ujemna).
Okazuje się jednak, że w powyższym przykładzie Ania mogła zagrać
lepiej. Wzięcie
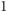 w pierwszym ruchu powoduje, że Bartek bierze
w pierwszym ruchu powoduje, że Bartek bierze
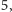 z kolei Ania bierze
z kolei Ania bierze
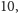 a Bartek
a Bartek
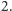 W takiej sytuacji
przewaga Ani wynosi
W takiej sytuacji
przewaga Ani wynosi
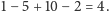

Naiwna strategia zachłanna nie zawsze się opłaca, potrzebujemy zatem czegoś
lepszego. Okazuje się, że jeśli liczba monet
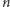 jest parzysta, to Ania ma
bardzo prostą strategię, dzięki której może zawsze uzyskać nieujemną
przewagę, niezależnie od nominałów monet. Wyróżnijmy co drugą monetę
w rzędzie:
jest parzysta, to Ania ma
bardzo prostą strategię, dzięki której może zawsze uzyskać nieujemną
przewagę, niezależnie od nominałów monet. Wyróżnijmy co drugą monetę
w rzędzie:
Zauważmy, że istnieje strategia, w której Ania zabierze wszystkie wyróżnione monety. Istotnie, przed każdym ruchem Ani dokładnie na jednym krańcu będzie wyróżniona moneta (i tę monetę zabierze Ania), zaś przed każdym ruchem Bartka żadna z monet na krańcach nie będzie wyróżniona (więc Bartek nie będzie miał szans zabrać żadnej wyróżnionej monety).
Ania ma jednak wybór: może wyróżnić albo monety na pozycjach nieparzystych, albo monety na pozycjach parzystych. Oczywiście, wybierze ona ten wariant, który da jej większą sumę nominałów.
Jasne jest, że suma ta będzie równa co najmniej połowie całkowitej sumy nominałów.
Czytelnicy zechcą sprawdzić, że dla poniższego przykładu z bardziej „egzotycznymi” nominałami

Ciąg (*)

Ania może uzyskać przewagę równą
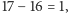 zabierając monety
z pozycji parzystych. Pytanie brzmi, czy ta strategia jest optymalna, tzn. czy
gwarantuje Ani najlepszy możliwy wynik? Spróbujmy podejść do sprawy
metodycznie. Oznaczmy wartości kolejnych nominałów w rzędzie przez
zabierając monety
z pozycji parzystych. Pytanie brzmi, czy ta strategia jest optymalna, tzn. czy
gwarantuje Ani najlepszy możliwy wynik? Spróbujmy podejść do sprawy
metodycznie. Oznaczmy wartości kolejnych nominałów w rzędzie przez
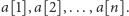 Zauważmy, że w dowolnym momencie gry na
stole znajduje się spójny podciąg monet. Dla ustalenia uwagi niech będą to
monety na pozycjach o numerach
Zauważmy, że w dowolnym momencie gry na
stole znajduje się spójny podciąg monet. Dla ustalenia uwagi niech będą to
monety na pozycjach o numerach
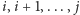 (dla
(dla
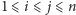 ).
Oznaczmy przez
).
Oznaczmy przez
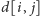 maksymalną możliwą do uzyskania przewagę dla
gracza, który w tej sytuacji wykonuje ruch – powiedzmy, że będzie to Ania. Ma
ona do wyboru dwie możliwości. Wzięcie monety z lewego krańca
(o numerze
maksymalną możliwą do uzyskania przewagę dla
gracza, który w tej sytuacji wykonuje ruch – powiedzmy, że będzie to Ania. Ma
ona do wyboru dwie możliwości. Wzięcie monety z lewego krańca
(o numerze
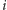 ) spowoduje przejście do sytuacji, w której na
stole znajdują się monety o numerach
) spowoduje przejście do sytuacji, w której na
stole znajdują się monety o numerach
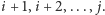 W tej
sytuacji przewaga przeciwnika (Bartka) wyniesie
W tej
sytuacji przewaga przeciwnika (Bartka) wyniesie
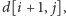 zatem
przewaga Ani będzie równa
zatem
przewaga Ani będzie równa
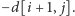 Dodając zysk
Dodając zysk
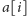 z
z
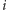 -tej monety, widzimy, że po tym ruchu przewaga Ani wyniesie
-tej monety, widzimy, że po tym ruchu przewaga Ani wyniesie
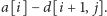 Rozumując analogicznie, otrzymujemy, że wzięcie
monety z prawego krańca (o numerze
Rozumując analogicznie, otrzymujemy, że wzięcie
monety z prawego krańca (o numerze
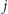 ) daje jej przewagę
) daje jej przewagę
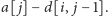 Zatem wartości tablicy
Zatem wartości tablicy
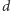 można wyznaczyć
za pomocą następującej rekurencji:
można wyznaczyć
za pomocą następującej rekurencji:

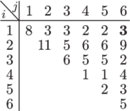
Na marginesie znajduje się tablica dla naszego ciągu (*). Przykładowo, aby wyznaczyć wyróżniony element tablicy, obliczamy

Tak więc przewaga Ani w naszym przykładzie wynosi
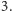 Można ją
uzyskać, biorąc w pierwszym ruchu monetę o nominale
Można ją
uzyskać, biorąc w pierwszym ruchu monetę o nominale
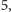 a dalej
grając zachłannie.
a dalej
grając zachłannie.
Tabelka koduje optymalną strategię dla całej gry. Problematyczne jest jednak to,
że do jej wyznaczenia potrzebujemy wykonać
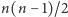 obliczeń,
nawet jeśli chcemy wyznaczyć tylko pierwszy ruch Ani lub jej przewagę
w grze. Podamy teraz prostszy sposób na wyznaczanie tych rzeczy.
obliczeń,
nawet jeśli chcemy wyznaczyć tylko pierwszy ruch Ani lub jej przewagę
w grze. Podamy teraz prostszy sposób na wyznaczanie tych rzeczy.
Znajdźmy w ciągu trzy monety na kolejnych pozycjach
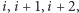 których
nominały spełniają nierówności
których
nominały spełniają nierówności
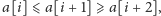 i zastąpmy je
jedną monetą o nominale
i zastąpmy je
jedną monetą o nominale
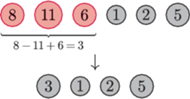
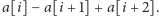 Jeśli istnieje więcej
takich trójek, to wybieramy dowolną z nich. Okazuje się (choć nie jest to ani
oczywiste, ani łatwe do uzasadnienia), że taka operacja nie zmienia przewagi
Ani. Stosując ją w naszym przykładzie (*), dostajemy:
Jeśli istnieje więcej
takich trójek, to wybieramy dowolną z nich. Okazuje się (choć nie jest to ani
oczywiste, ani łatwe do uzasadnienia), że taka operacja nie zmienia przewagi
Ani. Stosując ją w naszym przykładzie (*), dostajemy:
Jeśli ciąg nominałów jest bitoniczny (tzn. do pewnego momentu malejący,
a dalej rosnący – czyli nie uda się znaleźć trzech monet spełniających
powyższy warunek), to w takim przypadku działa już strategia zachłanna. Jest
tak dlatego, że niezależnie od kolejnych ruchów największa moneta będzie
zawsze znajdowała się na jednym z krańców ciągu. Zatem przewagę Ani
w przypadku ciągu bitonicznego bardzo łatwo obliczyć – wystarczy zsumować
liczby w porządku nierosnącym, biorąc co drugą liczbę ze znakiem minus.
W naszym przypadku będzie to
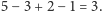
Czytelnicy zechcą sprawdzić, że w przykładzie

po zastosowaniu trzech operacji uzyskujemy bitoniczny ciąg

zatem i tym razem przewaga wynosi
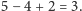
A co z wyznaczeniem optymalnego ruchu? Otóż, jeśli w bitonicznym ciągu,
powstałym po serii operacji, lewy nominał wynosi co najmniej tyle ile prawy
(a zatem wzięcie monety z lewego krańca jest optymalnym ruchem), to
również w pierwotnym ciągu wzięcie monety z lewego krańca jest
optymalnym ruchem. Analogicznie w przypadku prawego krańca. Zatem
w ciągu (**) wzięcie
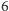 z lewego krańca jest optymalne, gdyż w ciągu
bitonicznym nominał na lewym krańcu jest większy niż ten na prawym
z lewego krańca jest optymalne, gdyż w ciągu
bitonicznym nominał na lewym krańcu jest większy niż ten na prawym
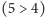 .
.
Ostatecznie otrzymujemy przepis, który pozwala nam wyznaczyć optymalny
ruch i wymaga jedynie liczby obliczeń rzędu