Zadanie ZF-840
o zadaniu...
- Publikacja w Delcie: wrzesień 2013
- Publikacja elektroniczna: 31-08-2013
W środku sfery całkowicie pochłaniającej dochodzące do niej światło umieszczono lampę sodową. Lampa emituje światło z mocą 100 W. Przyjmując, że emitowane jest wyłącznie światło o długości fali 590 nm, obliczyć, ile fotonów w jednostce czasu pochłania sfera.
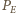 do energii
do energii
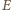 emitowanego
fotonu. Ponieważ
emitowanego
fotonu. Ponieważ
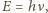 więc
więc
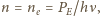 gdzie
gdzie
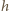 jest
stałą Plancka, a
jest
stałą Plancka, a
 częstością emitowanego światła. Podstawiając
częstością emitowanego światła. Podstawiając
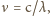 gdzie c jest prędkością światła, a
gdzie c jest prędkością światła, a
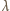 długością jego fali,
otrzymujemy ostatecznie
długością jego fali,
otrzymujemy ostatecznie
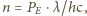 co dla wielkości danych
w zadaniu daje
co dla wielkości danych
w zadaniu daje
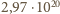 fotonów na sekundę.
fotonów na sekundę.
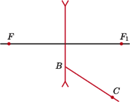
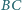 wychodzącego
z soczewki rozpraszającej, której ogniska znajdują się w punktach
wychodzącego
z soczewki rozpraszającej, której ogniska znajdują się w punktach
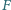 i
i
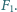 Znaleźć metodą geometryczną bieg promienia padającego na
soczewkę w punkcie
Znaleźć metodą geometryczną bieg promienia padającego na
soczewkę w punkcie
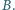
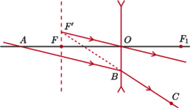
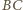 (rysunek) pochodzi z wiązki
promieni równoległych padających na soczewkę.
(rysunek) pochodzi z wiązki
promieni równoległych padających na soczewkę.
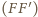 . W tym samym punkcie
. W tym samym punkcie
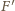 przetnie
więc płaszczyznę ogniskową, pochodzący z tej samej wiązki równoległej,
promień
przetnie
więc płaszczyznę ogniskową, pochodzący z tej samej wiązki równoległej,
promień
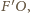 który nie zmienia swojego kierunku bo przechodzi przez
środek soczewki. Ponieważ promienie
który nie zmienia swojego kierunku bo przechodzi przez
środek soczewki. Ponieważ promienie
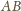 i
i
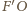 pochodzą z tej
samej wiązki równoległej, więc bieg promienia
pochodzą z tej
samej wiązki równoległej, więc bieg promienia
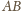 znajdujemy,
wykreślając prostą równoległą do
znajdujemy,
wykreślając prostą równoległą do
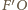 przechodzącą przez punkt
przechodzącą przez punkt
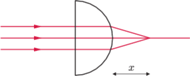
 skupia się w odległości
skupia się w odległości
 od powierzchni wypukłej.
W jakiej odległości od powierzchni płaskiej skupią się promienie, jeżeli wiązkę
światła przepuścimy przez półkulę z drugiej strony?
od powierzchni wypukłej.
W jakiej odległości od powierzchni płaskiej skupią się promienie, jeżeli wiązkę
światła przepuścimy przez półkulę z drugiej strony?
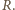 Gdy wiązka pada
prostopadle na płaską powierzchnię szkła, biegnie przez szkło bez zmiany
kierunku. Odległość
Gdy wiązka pada
prostopadle na płaską powierzchnię szkła, biegnie przez szkło bez zmiany
kierunku. Odległość
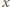 nie zmieni się, gdy wiązkę przepuścimy przez
cienką soczewkę płasko-wypukłą ze szkła o promieniu krzywizny
nie zmieni się, gdy wiązkę przepuścimy przez
cienką soczewkę płasko-wypukłą ze szkła o promieniu krzywizny
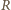 umieszczoną w powietrzu (
umieszczoną w powietrzu (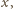 mamy więc związek
mamy więc związek
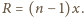
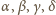 kąty padania i załamania przy przechodzeniu światła
z jednego ośrodka do drugiego, jak na
kąty padania i załamania przy przechodzeniu światła
z jednego ośrodka do drugiego, jak na 
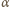 jest kątem zewnętrznym w trójkącie
jest kątem zewnętrznym w trójkącie
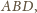 zatem
zatem
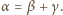 Niech
Niech
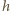 będzie odległością promienia wychodzącego
z półkuli od osi optycznej. Stosując twierdzenie sinusów do trójkąta
będzie odległością promienia wychodzącego
z półkuli od osi optycznej. Stosując twierdzenie sinusów do trójkąta
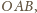 otrzymujemy:
otrzymujemy:
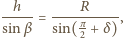 a w przybliżeniu
a w przybliżeniu
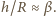 Szukaną odległość
Szukaną odległość
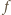 punktu skupienia promieni od
powierzchni płaskiej dostajemy ze związków:
punktu skupienia promieni od
powierzchni płaskiej dostajemy ze związków:
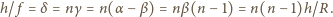
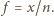
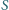 oświetla przezroczystą kulkę. Dzięki
przesłonie padają na nią tylko promienie biegnące blisko osi
oświetla przezroczystą kulkę. Dzięki
przesłonie padają na nią tylko promienie biegnące blisko osi
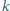 łączącej
łączącej
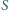 ze środkiem kulki. W efekcie w odległości
ze środkiem kulki. W efekcie w odległości
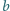 za kulką powstał
obraz źródła
za kulką powstał
obraz źródła
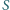 . Kulkę przecięto przez środek prostopadle do
. Kulkę przecięto przez środek prostopadle do
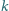 i powierzchnię przecięcia posrebrzono. Gdzie teraz znajduje się obraz
źródła
i powierzchnię przecięcia posrebrzono. Gdzie teraz znajduje się obraz
źródła
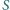 ?
?
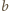 od kulki, ale po jej drugiej stronie.
od kulki, ale po jej drugiej stronie.
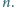 Dla jakiej najmniejszej wartości
Dla jakiej najmniejszej wartości
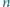 ani jeden promień światła
nie wydostanie się przez powierzchnię boczną na zewnątrz?
ani jeden promień światła
nie wydostanie się przez powierzchnię boczną na zewnątrz?
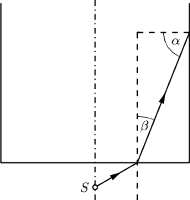
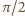 na dno
cylindra kąt padania
na dno
cylindra kąt padania
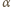 na powierzchnię boczną będzie spełniał
nierówność
na powierzchnię boczną będzie spełniał
nierówność
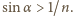
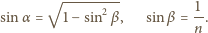
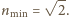
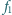 i
i
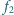 są
odległe o
są
odległe o
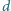 i wykonane z tego samego szkła. Jaki warunek muszą
spełniać podane parametry, aby ogniskowa zespołu nie zależała od długości
fali (aby układ był achromatyczny)? Zmiany współczynnika załamania
są niewielkie.
i wykonane z tego samego szkła. Jaki warunek muszą
spełniać podane parametry, aby ogniskowa zespołu nie zależała od długości
fali (aby układ był achromatyczny)? Zmiany współczynnika załamania
są niewielkie.
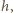 a wychodząc z układu przecina oś pod kątem
a wychodząc z układu przecina oś pod kątem
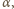 to ogniskowa wynosi
to ogniskowa wynosi
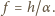
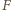 układu jest dość standardowe i nie będziemy
go powtarzać. Otrzymuje się
układu jest dość standardowe i nie będziemy
go powtarzać. Otrzymuje się
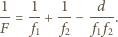
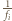 w postaci
w postaci
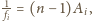 gdzie
gdzie
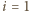 lub 2,
lub 2,
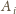 nie zależy od
nie zależy od
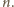 Przy niewielkiej zmianie
Przy niewielkiej zmianie
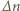 zmiana
zdolności skupiającej układu
zmiana
zdolności skupiającej układu
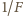 wynosi
wynosi
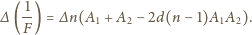
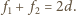
 wykonano niewielki otworek o promieniu
wykonano niewielki otworek o promieniu
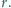 Wzdłuż osi
otworka rozchodzi się cienki promień światła. Jaki musi być poziom cieczy
Wzdłuż osi
otworka rozchodzi się cienki promień światła. Jaki musi być poziom cieczy
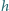 nad otworkiem, aby promień mógł wyjść ze strugi cieczy, ani razu
nie dokonując całkowicie wewnętrznego odbicia? Założyć, że współczynnik
załamania
nad otworkiem, aby promień mógł wyjść ze strugi cieczy, ani razu
nie dokonując całkowicie wewnętrznego odbicia? Założyć, że współczynnik
załamania
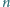 cieczy jest dostatecznie duży. Pominąć zmianę przekroju
poprzecznego cieczy.
cieczy jest dostatecznie duży. Pominąć zmianę przekroju
poprzecznego cieczy.
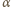 z poziomym
promieniem światła. Z drugiej strony kąt ten jest wyznaczony przez stosunek
składowej poziomej i pionowej cieczy:
z poziomym
promieniem światła. Z drugiej strony kąt ten jest wyznaczony przez stosunek
składowej poziomej i pionowej cieczy:
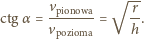
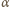 jest kątem granicznym, jeśli
jest kątem granicznym, jeśli
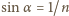 , zatem:
, zatem:
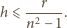
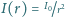 .
Jak zmienia się ta zależność, gdy w powietrzu znajduje się pochłaniający
światło pył o koncentracji
.
Jak zmienia się ta zależność, gdy w powietrzu znajduje się pochłaniający
światło pył o koncentracji
 i polu powierzchni drobiny
i polu powierzchni drobiny
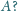
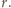 Kulę
dzielimy za pomocą współśrodkowych sfer na
Kulę
dzielimy za pomocą współśrodkowych sfer na
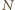 części o jednakowej
grubości
części o jednakowej
grubości
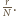 W
W
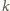 -tej części, licząc od środka, znajduje się
-tej części, licząc od środka, znajduje się
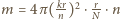 drobin pyłu, które zasłaniają powierzchnię
drobin pyłu, które zasłaniają powierzchnię
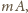 czyli
czyli
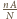 całości powierzchni sfery. Drobiny w różnych warstwach
ustawione są przypadkowo i niezależnie od siebie, więc całkowita niezasłonięta
powierzchnia to
całości powierzchni sfery. Drobiny w różnych warstwach
ustawione są przypadkowo i niezależnie od siebie, więc całkowita niezasłonięta
powierzchnia to
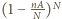 całej sfery, co po przejściu do granicy
całej sfery, co po przejściu do granicy
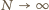 daje
daje
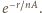 Po podzieleniu na jednostkę powierzchni
otrzymujemy
Po podzieleniu na jednostkę powierzchni
otrzymujemy
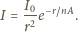
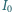 pada na kulkę o promieniu
pada na kulkę o promieniu
 ze szkła
o współczynniku załamania
ze szkła
o współczynniku załamania
 W odległości
W odległości
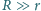 od kulki
znajduje się ekran prostopadły do wiązki padającej, ale oświetlony tylko przez
światło przechodzące przez kulkę. Jeśli można pominąć efekty dyfrakcyjne i
odbicie światła od szkła, to jakie jest natężenie światła padającego na środek
ekranu?
od kulki
znajduje się ekran prostopadły do wiązki padającej, ale oświetlony tylko przez
światło przechodzące przez kulkę. Jeśli można pominąć efekty dyfrakcyjne i
odbicie światła od szkła, to jakie jest natężenie światła padającego na środek
ekranu?

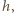 pada
na jej powierzchnię pod kątem
pada
na jej powierzchnię pod kątem
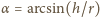 i załamuje się pod kątem
i załamuje się pod kątem
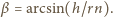 Ponieważ przy wyjściu z kulki kąty są te same, więc
kąt odchylenia tego promienia od kierunku początkowego jest równy
Ponieważ przy wyjściu z kulki kąty są te same, więc
kąt odchylenia tego promienia od kierunku początkowego jest równy
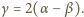 Rozpatrując promienie padające na ekran w pobliżu
środka, należy przyjąć, że kąty są małe, tzn.
Rozpatrując promienie padające na ekran w pobliżu
środka, należy przyjąć, że kąty są małe, tzn.
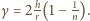 Gdy
spełniony jest warunek
Gdy
spełniony jest warunek
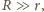 promienie odchylone o
promienie odchylone o
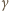 padają na
ekran w odległości
padają na
ekran w odległości
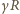 od środka. Widzimy, że wiązka o polu
przekroju
od środka. Widzimy, że wiązka o polu
przekroju
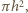 której moc wynosi
której moc wynosi
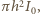 oświetla na ekranie
koło o polu
oświetla na ekranie
koło o polu
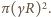 Szukane natężenie oświetlenia środka ekranu
wynosi więc
Szukane natężenie oświetlenia środka ekranu
wynosi więc
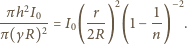
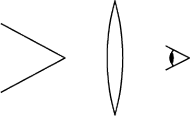
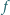 widzimy obraz pozorny
stożka, którego oś pokrywa się z osią soczewki. Kąt rozwarcia stożka
wynosi
widzimy obraz pozorny
stożka, którego oś pokrywa się z osią soczewki. Kąt rozwarcia stożka
wynosi
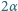 , a jego wierzchołek jest odległy od soczewki o
, a jego wierzchołek jest odległy od soczewki o
 . Ile
wynosi kąt rozwarcia obrazu stożka
. Ile
wynosi kąt rozwarcia obrazu stożka
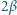 ?
?
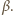 Oznaczmy przez
Oznaczmy przez
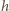 wysokość, na której następuje załamanie tego promienia,
a przez
wysokość, na której następuje załamanie tego promienia,
a przez
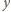 odległość obrazu wierzchołka stożka od soczewki.
Z równań
odległość obrazu wierzchołka stożka od soczewki.
Z równań