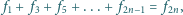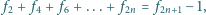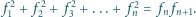Zadanie ZM-1421
o zadaniu...
- Publikacja w Delcie: maj 2014
- Publikacja elektroniczna: 01-05-2014
Udowodnić, że dla dodatnich liczb całkowitych
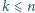 prawdziwa jest
nierówność
prawdziwa jest
nierówność
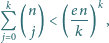
gdzie
 to stała zdefiniowana np. jako
to stała zdefiniowana np. jako
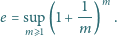
Udowodnić, że dla dodatnich liczb całkowitych
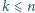 prawdziwa jest
nierówność
prawdziwa jest
nierówność
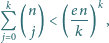
gdzie
 to stała zdefiniowana np. jako
to stała zdefiniowana np. jako
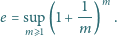
Udowodnić, że dla każdej liczby naturalnej
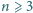 zachodzi
podzielność
zachodzi
podzielność
Zadanie 678 zaproponował pan Witold Bednarek z Łodzi.
Czy istnieją takie trzy różne liczby pierwsze
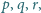 że liczba
że liczba
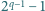 dzieli się przez
dzieli się przez
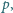 liczba
liczba
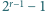 dzieli się przez
dzieli się przez
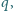 zaś liczba
zaś liczba
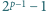 dzieli się przez
dzieli się przez
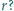
Czy istnieją cztery kolejne liczby całkowite dodatnie, których iloczyn,
powiększony o
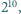 jest kwadratem liczby całkowitej? Podać wszystkie
rozwiązania (jeśli istnieją).
jest kwadratem liczby całkowitej? Podać wszystkie
rozwiązania (jeśli istnieją).
Dana jest liczba pierwsza
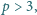 taka, że
taka, że
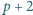 też jest pierwsza.
Na tablicy napisano liczby
też jest pierwsza.
Na tablicy napisano liczby
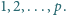 W każdym kroku wybieramy
jedną z nich, powiedzmy
W każdym kroku wybieramy
jedną z nich, powiedzmy
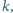 po czym zmazujemy wszystkie dzielniki
liczby
po czym zmazujemy wszystkie dzielniki
liczby
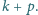 Udowodnić, że w ten sposób nigdy nie zmażemy
wszystkich liczb napisanych na tablicy.
Udowodnić, że w ten sposób nigdy nie zmażemy
wszystkich liczb napisanych na tablicy.
Udowodnić, że równanie
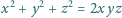
nie ma rozwiązania w liczbach całkowitych dodatnich.
Udowodnić, że istnieje liczba
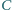 o następującej własności: jeśli
równanie
o następującej własności: jeśli
równanie
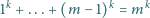
ma rozwiązanie dla pewnych liczb naturalnych
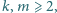 to
to
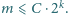
Dana jest liczba naturalna
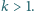 Znaleźć wszystkie liczby naturalne
Znaleźć wszystkie liczby naturalne
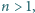 spełniające nierówność
spełniające nierówność

gdzie
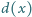 oznacza liczbę dodatnich dzielników liczby naturalnej
oznacza liczbę dodatnich dzielników liczby naturalnej

Dana jest liczba nieparzysta
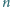 i liczby całkowite dodatnie względnie
pierwsze
i liczby całkowite dodatnie względnie
pierwsze
 i
i
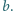 Udowodnić, że liczba
Udowodnić, że liczba
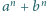 jest
podzielna przez
jest
podzielna przez
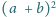 wtedy i tylko wtedy, gdy liczba
wtedy i tylko wtedy, gdy liczba
 jest
podzielna przez
jest
podzielna przez
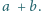
Zadanie 656 zaproponował pan Piotr Zarzycki z Gdańska.
Dana jest liczba naturalna
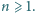 Niech
Niech
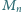 będzie liczbą
naturalną, której zapis dziesiętny składa się z
będzie liczbą
naturalną, której zapis dziesiętny składa się z
 dziewiątek:
dziewiątek:
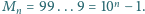 Znaleźć najmniejszą jej wielokrotność,
w której zapisie dziesiętnym cyfra 9 nie występuje.
Znaleźć najmniejszą jej wielokrotność,
w której zapisie dziesiętnym cyfra 9 nie występuje.
Wykazać, że nie istnieje liczba pierwsza
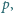 dla której
dla której
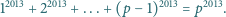
Znaleźć wszystkie pary liczb całkowitych
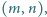 dla których
liczby
dla których
liczby

są także całkowite.
Niech
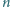 będzie liczbą pięciocyfrową w zapisie dziesiętnym (pierwsza
cyfra jest różna od
będzie liczbą pięciocyfrową w zapisie dziesiętnym (pierwsza
cyfra jest różna od
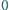 ) i niech
) i niech
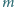 będzie liczbą czterocyfrową
powstałą z
będzie liczbą czterocyfrową
powstałą z
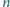 przez wyrzucenie jej środkowej cyfry. Znaleźć wszystkie
takie liczby
przez wyrzucenie jej środkowej cyfry. Znaleźć wszystkie
takie liczby
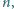 że liczba
że liczba
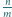 jest całkowita.
jest całkowita.
Dany jest przedział otwarty, którego końcami są kwadraty dwóch kolejnych
liczb naturalnych, większych od 1. Dowieść, że w tym przedziale
można znaleźć trzy różne liczby naturalne
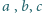 takie, że
takie, że
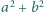 dzieli się przez
dzieli się przez

Zadanie 648 zaproponował pan Tomasz Ordowski.
Niech
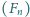 będzie ciągiem Fibonacciego:
będzie ciągiem Fibonacciego:

Udowodnić, że ciąg
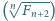 jest malejący.
jest malejący.
Udowodnij, że jeśli
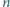 jest dodatnią liczbą całkowitą, to liczba
jest dodatnią liczbą całkowitą, to liczba
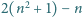 nie jest kwadratem liczby całkowitej.
nie jest kwadratem liczby całkowitej.
Niech
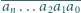 oznacza liczbę, której cyfrą jedności w zapisie
dziesiętnym jest
oznacza liczbę, której cyfrą jedności w zapisie
dziesiętnym jest
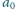 , cyfrą dziesiątek –
, cyfrą dziesiątek –
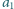 , cyfrą setek –
, cyfrą setek –
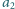 ,
itd. Znaleźć wszystkie liczby czterocyfrowe
,
itd. Znaleźć wszystkie liczby czterocyfrowe
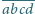 , które spełniają
równość
, które spełniają
równość

Liczba
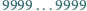 jest zapisana za pomocą
jest zapisana za pomocą
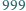 dziewiątek. Ile
wynosi suma cyfr kwadratu tej liczby?
dziewiątek. Ile
wynosi suma cyfr kwadratu tej liczby?
Wykaż, że dla każdego naturalnego
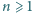 zachodzą następujące
równości:
zachodzą następujące
równości: