Zadanie ZM-1499
o zadaniu...
- Publikacja w Delcie: lipiec 2016
- Publikacja elektroniczna: 1 lipca 2016
Czy istnieje wielokrotność liczby 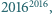 której zapis w systemie dziesiętnym zawiera wszystkie dziesięć cyfr?
której zapis w systemie dziesiętnym zawiera wszystkie dziesięć cyfr?
Czy istnieje wielokrotność liczby 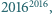 której zapis w systemie dziesiętnym zawiera wszystkie dziesięć cyfr?
której zapis w systemie dziesiętnym zawiera wszystkie dziesięć cyfr?
Czy każdy ściśle rosnący ciąg arytmetyczny o wyrazach całkowitych ma wyraz, będący jednocześnie pewnym wyrazem ciągu Fibonacciego 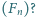

Zadanie 722 zaproponował pan Witold Bednarek z Łodzi.
Rozwiązać równanie 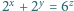 w liczbach całkowitych dodatnich
w liczbach całkowitych dodatnich 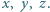
Wyznaczyć największą liczbę naturalną 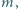 dla której istnieją takie liczby naturalne
dla której istnieją takie liczby naturalne 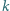 i
i 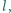 że spełnione jest równanie
że spełnione jest równanie
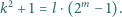
W wierzchołkach dwunastościanu foremnego umieszczamy parami różne liczby naturalne, a następnie każdej krawędzi przypisujemy największy wspólny dzielnik liczb z jej końców. Czy możemy zrobić to w taki sposób, by suma liczb w wierzchołkach była równa sumie liczb na krawędziach?
Udowodnić, że istnieje 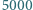 liczb
liczb 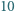 -cyfrowych podzielnych przez
-cyfrowych podzielnych przez 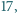 takich że każdą z nich można otrzymać z dowolnej z pozostałych poprzez zmianę kolejności cyfr.
takich że każdą z nich można otrzymać z dowolnej z pozostałych poprzez zmianę kolejności cyfr.
Znaleźć liczbę wielokrotności 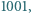 które można zapisać w postaci
które można zapisać w postaci 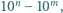 gdzie
gdzie  oraz
oraz 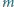 są liczbami całkowitymi spełniającymi
są liczbami całkowitymi spełniającymi 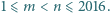
Rozstrzygnąć, czy istnieją liczby naturalne 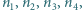 wszystkie większe od
wszystkie większe od 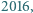 spełniające równanie
spełniające równanie

Dane są takie liczby całkowite dodatnie 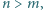 że liczby
że liczby 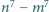 oraz
oraz 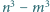 są względnie pierwsze. Wykaż, że liczby
są względnie pierwsze. Wykaż, że liczby 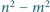 i
i 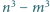 są również względnie pierwsze.
są również względnie pierwsze.
Dane są dwie różne liczby całkowite dodatnie 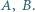 Wykazać, że zbiór wszystkich liczb całkowitych nieujemnych może być przedstawiony jako suma rozłącznych zbiorów trójelementowych, przy czym w każdym z tych zbiorów liczba środkowa (co do wielkości) różni się od jednej z dwóch pozostałych liczb o
Wykazać, że zbiór wszystkich liczb całkowitych nieujemnych może być przedstawiony jako suma rozłącznych zbiorów trójelementowych, przy czym w każdym z tych zbiorów liczba środkowa (co do wielkości) różni się od jednej z dwóch pozostałych liczb o 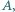 zaś od drugiej o
zaś od drugiej o 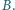
Zadanie 714 zaproponował pan Witold Bednarek z Łodzi.
Niech 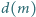 oznacza liczbę dodatnich dzielników liczby naturalnej
oznacza liczbę dodatnich dzielników liczby naturalnej 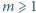
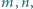 spełniających równanie
spełniających równanie 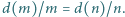
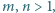 spełniających równanie
spełniających równanie 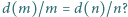
Wykaż, że 56 nie jest trzecią potęgą liczby naturalnej.
Znajdź wszystkie trójki dodatnich liczb całkowitych 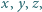 dla których
dla których 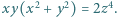
Znajdź wszystkie pary liczb całkowitych 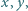 dla których
dla których 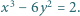
Wykazać, że jeśli liczby całkowite dodatnie 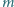 i
i  spełniają
spełniają 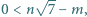 to wówczas
to wówczas 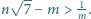
Dany jest ciąg dodatnich liczb całkowitych 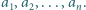 Ruch polega na wyborze dwóch takich indeksów
Ruch polega na wyborze dwóch takich indeksów 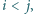 że
że 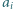 nie dzieli
nie dzieli 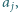 i zastąpieniu liczb
i zastąpieniu liczb 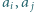 przez odpowiednio ich największy wspólny dzielnik i najmniejszą wspólną wielokrotność. Udowodnić, że nie jest możliwe wykonanie nieskończenie wielu ruchów.
przez odpowiednio ich największy wspólny dzielnik i najmniejszą wspólną wielokrotność. Udowodnić, że nie jest możliwe wykonanie nieskończenie wielu ruchów.
Udowodnić, że nie istnieje 11 liczb pierwszych mniejszych od 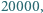 które tworzą ciąg arytmetyczny.
które tworzą ciąg arytmetyczny.
Czy istnieje nieskończony ciąg 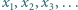 o wyrazach całkowitych dodatnich, w którym każda dodatnia liczba całkowita występuje jednokrotnie, przy czym dla każdego
o wyrazach całkowitych dodatnich, w którym każda dodatnia liczba całkowita występuje jednokrotnie, przy czym dla każdego  suma
suma 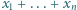 jest podzielna przez
jest podzielna przez 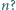
Dane są dodatnie liczby całkowite nieparzyste 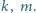 Niech
Niech 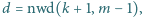
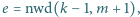
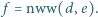 Dowieść, że liczba
Dowieść, że liczba 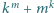 dzieli się przez
dzieli się przez 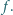
Wyznacz wszystkie liczby naturalne 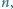 dla których liczba
dla których liczba

jest pierwsza.