Zadanie ZM-830
o zadaniu...
- Publikacja w Delcie: grudzień 1997
- Publikacja elektroniczna: 24 sierpnia 2017
Znaleźć największą liczbę naturalną 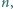 dla której
dla której 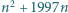 jest kwadratem liczby naturalnej.
jest kwadratem liczby naturalnej.
Znaleźć największą liczbę naturalną 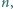 dla której
dla której 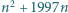 jest kwadratem liczby naturalnej.
jest kwadratem liczby naturalnej.
Wyznaczyć największą liczbę naturalną 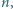 dla której istnieją czteroelementowe zbiory
dla której istnieją czteroelementowe zbiory 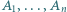 o następującej własności: każdy zbiór
o następującej własności: każdy zbiór 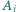 ma z każdym innym zbiorem
ma z każdym innym zbiorem 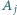 dokładnie jeden element wspólny, ale nie istnieje wspólny element wszystkich zbiorów
dokładnie jeden element wspólny, ale nie istnieje wspólny element wszystkich zbiorów 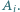
Dana jest liczba 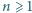 oraz pewien zbiór
oraz pewien zbiór 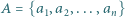 dodatnich liczb całkowitych. Na okręgu wyróżniono
dodatnich liczb całkowitych. Na okręgu wyróżniono 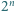 punktów i każdemu z nich przyporządkowano jedną z liczb ze zbioru
punktów i każdemu z nich przyporządkowano jedną z liczb ze zbioru 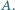 Udowodnić, że iloczyn liczb znajdujących się na pewnym łuku tego okręgu jest kwadratem liczby całkowitej.
Udowodnić, że iloczyn liczb znajdujących się na pewnym łuku tego okręgu jest kwadratem liczby całkowitej.
Niech 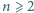 będzie liczbą całkowitą. Znaleźć liczbę przedstawień liczby
będzie liczbą całkowitą. Znaleźć liczbę przedstawień liczby 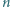 w postaci sumy pewnej liczby dodatnich całkowitych składników, pośród których jest parzysta liczba liczb parzystych.
w postaci sumy pewnej liczby dodatnich całkowitych składników, pośród których jest parzysta liczba liczb parzystych.
Zadanie 744 zostało opracowane na podstawie propozycji, którą przysłał pan Paweł Kubit z Krakowa.
Dana jest liczba całkowita 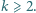 Niech
Niech 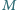 będzie takim zbiorem dodatnich liczb całkowitych, że dla każdej pary różnych liczb
będzie takim zbiorem dodatnich liczb całkowitych, że dla każdej pary różnych liczb 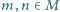 zachodzi nierówność
zachodzi nierówność 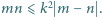 Wykazać, że zbiorze
Wykazać, że zbiorze 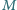 jest nie więcej niż
jest nie więcej niż 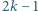 liczb. Czy dla każdej liczby
liczb. Czy dla każdej liczby 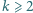 istnieje
istnieje 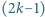 -elementowy zbiór
-elementowy zbiór 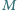 o podanej własności?
o podanej własności?
Zadanie 742 zaproponował pan Tomasz Ordowski.
Niech 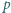 będzie liczbą pierwszą postaci
będzie liczbą pierwszą postaci 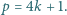 Dowieść, że istnieje liczba całkowita dodatnia
Dowieść, że istnieje liczba całkowita dodatnia 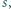 mniejsza od
mniejsza od 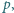 dla której różnica
dla której różnica 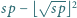 jest kwadratem liczby całkowitej dodatniej.
jest kwadratem liczby całkowitej dodatniej.
Udowodnić, że jeżeli dla pewnej liczby naturalnej 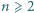 liczba
liczba 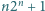 jest pierwsza, to liczby
jest pierwsza, to liczby 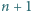 oraz
oraz 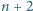 są złożone.
są złożone.
Wyznacz liczbę podzbiorów zbioru 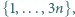 które nie zawierają dwóch liczb różniących się o
które nie zawierają dwóch liczb różniących się o 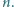
Udowodnij tożsamość 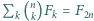 (
( 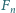 oznacza
oznacza  -tą liczbę Fibonacciego, czyli rozwiązanie równania rekurencyjnego
-tą liczbę Fibonacciego, czyli rozwiązanie równania rekurencyjnego 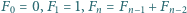 dla
dla 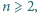 a zarazem liczbę pokryć paska
a zarazem liczbę pokryć paska 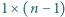 kwadratami
kwadratami 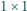 i prostokątami
i prostokątami 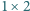 ).
).
Udowodnić, że dla każdego 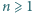 istnieje ciąg arytmetyczny
istnieje ciąg arytmetyczny  dodatnich liczb całkowitych, z których każda jest podzielna przez sumę swoich cyfr (w zapisie dziesiętnym).
dodatnich liczb całkowitych, z których każda jest podzielna przez sumę swoich cyfr (w zapisie dziesiętnym).
Wskazówka. W rozwiązaniu można skorzystać z twierdzenia o liczbach pierwszych, na przykład używając szacowania 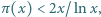 prawdziwego dla dostatecznie dużych
prawdziwego dla dostatecznie dużych 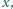 gdzie
gdzie 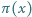 oznacza liczbę liczb pierwszych nie większych od
oznacza liczbę liczb pierwszych nie większych od 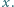
Zadanie 738 zaproponował pan Bartłomiej Pawlik z Limanowej.
Wypisując, jedna za drugą, wszystkie liczby całkowite dodatnie, mające (w systemie dziesiętnym) co najwyżej 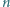 cyfr, piszemy łącznie
cyfr, piszemy łącznie 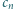 cyfr (np.
cyfr (np. 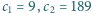 ); w tym
); w tym 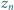 zer (np.
zer (np. 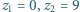 ). Czy równość
). Czy równość 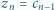 jest spełniona dla wszystkich liczb naturalnych
jest spełniona dla wszystkich liczb naturalnych 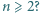
Przypuśćmy, że dla pewnej dodatniej liczby całkowitej 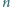 liczby
liczby 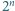 oraz
oraz 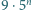 rozpoczynają się w zapisie dziesiętnym tą samą cyfrą. Jaka to cyfra?
rozpoczynają się w zapisie dziesiętnym tą samą cyfrą. Jaka to cyfra?
Każdą liczbę całkowitą większą od 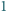 pomalowano na pewien kolor w taki sposób, że jeżeli dla pewnych dwóch liczb
pomalowano na pewien kolor w taki sposób, że jeżeli dla pewnych dwóch liczb 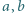 większych od
większych od 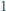 liczba
liczba 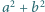 jest podzielna przez
jest podzielna przez 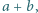 to
to 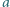 ma ten sam kolor, co
ma ten sam kolor, co 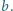 Jaka jest największa możliwa liczba kolorów użytych do pomalowania liczb?
Jaka jest największa możliwa liczba kolorów użytych do pomalowania liczb?
Udowodnij, że dla każdej niepodzielnej przez 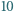 liczby naturalnej
liczby naturalnej 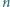 istnieje taka liczba naturalna
istnieje taka liczba naturalna 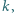 że pierwsza i ostatnia cyfra liczby
że pierwsza i ostatnia cyfra liczby 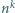 są równe.
są równe.
Zadanie 732 zaproponował pan Tomasz Ordowski.
Ciąg liczb naturalnych 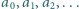 jest określony wzorem rekurencyjnym:
jest określony wzorem rekurencyjnym: 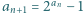 ; wyraz początkowy
; wyraz początkowy 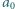 jest liczbą pierwszą. Dowieść, że dla każdego
jest liczbą pierwszą. Dowieść, że dla każdego 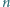 różnica
różnica 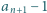 jest podzielna przez
jest podzielna przez 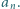
Znaleźć wszystkie liczby całkowite 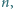 dla których liczba
dla których liczba 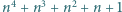 jest kwadratem liczby całkowitej.
jest kwadratem liczby całkowitej.
Obliczyć sumę
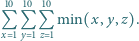
Trójkąt równoboczny o boku długości 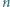 został podzielony (prostymi równoległymi do boków) na
został podzielony (prostymi równoległymi do boków) na 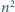 trójkącików o boku 1. Każdy wierzchołek powstałej siatki (tj. wierzchołek któregoś trójkącika) jest pomalowany na biało lub czarno. Wykonujemy ciąg ruchów. W jednym ruchu zmieniamy kolor wszystkich wierzchołków, leżących na jednej linii prostej, zawierającej bok któregoś trójkącika.
trójkącików o boku 1. Każdy wierzchołek powstałej siatki (tj. wierzchołek któregoś trójkącika) jest pomalowany na biało lub czarno. Wykonujemy ciąg ruchów. W jednym ruchu zmieniamy kolor wszystkich wierzchołków, leżących na jednej linii prostej, zawierającej bok któregoś trójkącika.
Wyznaczyć wszystkie liczby naturalne 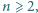 dla których - wychodząc od stanu: wszystkie wierzchołki białe - można dojść do stanu: dokładnie jeden wierzchołek czarny.
dla których - wychodząc od stanu: wszystkie wierzchołki białe - można dojść do stanu: dokładnie jeden wierzchołek czarny.
Zadanie 726 zaproponował pan Tomasz Ordowski.
Niech  będzie ustaloną liczbą całkowitą dodatnią. Dowieść, że istnieje nieujemna liczba całkowita
będzie ustaloną liczbą całkowitą dodatnią. Dowieść, że istnieje nieujemna liczba całkowita 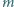 taka, że
taka, że 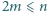 oraz różnica
oraz różnica 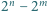 dzieli się przez
dzieli się przez 
Czy istnieje taka liczba 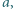 że jej suma cyfr w systemie dziesiętnym jest równa
że jej suma cyfr w systemie dziesiętnym jest równa 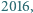 a suma cyfr liczby
a suma cyfr liczby 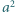 jest równa
jest równa