Piramida kwadratowych liczb»Zadanie 1
o zadaniu...
- Zadanie pochodzi z artykułu Piramida kwadratowych liczb
- Publikacja w Delcie: sierpień 2020
- Publikacja elektroniczna: 1 sierpnia 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (413 KB)
Udowodnić, że piramida o podstawie kwadratu ułożona z kul armatnich składa się z kwadratowej liczby kul wtedy i tylko wtedy, gdy bok jej podstawy ma długość 24 kul.
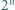 jedynek ma co najmniej
jedynek ma co najmniej 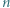 różnych dzielników pierwszych.
różnych dzielników pierwszych.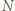 będzie liczbą składającą się w zapisie dziesiętnym z
będzie liczbą składającą się w zapisie dziesiętnym z 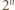 jedynek. Mamy
jedynek. Mamy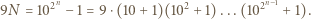
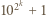 i
i 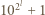 są względnie pierwsze dla
są względnie pierwsze dla 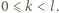 Załóżmy, że obie te liczby są podzielne przez liczbę pierwszą
Załóżmy, że obie te liczby są podzielne przez liczbę pierwszą 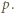 Oczywiście liczba
Oczywiście liczba 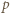 jest nieparzysta. Ponieważ
jest nieparzysta. Ponieważ 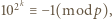 więc
więc 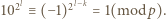 Skoro jednak
Skoro jednak 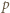 dzieli
dzieli 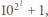 to
to 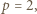 co przeczy wcześniej poczynionej uwadze o nieparzystości
co przeczy wcześniej poczynionej uwadze o nieparzystości 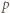 i kończy rozwiązanie zadania.
i kończy rozwiązanie zadania.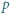
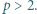

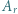
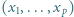
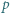 ), że
), że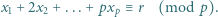
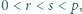

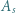
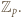
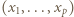


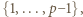
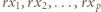
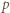
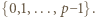
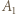 - czyli spełniała zależność
- czyli spełniała zależność 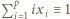 (mod
(mod 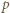 ) - to po pomnożeniu wszystkich jej wyrazów przez
) - to po pomnożeniu wszystkich jej wyrazów przez 
 - czyli permutację należącą do zbioru
- czyli permutację należącą do zbioru 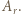
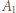
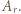
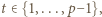
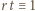 (mod
(mod 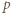 ) (taki element
) (taki element 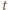
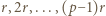
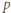
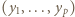
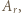
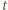
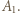
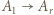 (mnożenie przez
(mnożenie przez  ) oraz
) oraz 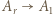 (mnożenie przez
(mnożenie przez 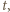
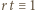 ) są wzajemnie odwrotne. To dowodzi, że zbiór
) są wzajemnie odwrotne. To dowodzi, że zbiór 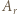
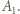
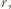
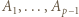
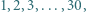 jeżeli podczas ważenia odważniki można układać tylko na jednej szalce.
jeżeli podczas ważenia odważniki można układać tylko na jednej szalce.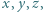 że
że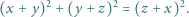
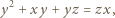
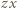 do obu stron daje
do obu stron daje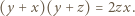
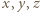 są nieparzyste, to lewa strona powyższej równości jest podzielna przez 4, w przeciwieństwie do prawej strony, co kończy rozwiązanie zadania.
są nieparzyste, to lewa strona powyższej równości jest podzielna przez 4, w przeciwieństwie do prawej strony, co kończy rozwiązanie zadania.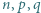 będą liczbami całkowitymi dodatnimi. Ciąg liczb całkowitych
będą liczbami całkowitymi dodatnimi. Ciąg liczb całkowitych 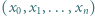 spełnia warunki:
spełnia warunki: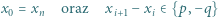
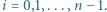 Udowodnić, że jeżeli
Udowodnić, że jeżeli 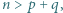 to istnieją takie
to istnieją takie 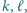 że
że 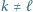 i
i 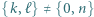 oraz
oraz 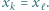
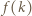 dla
dla 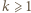 będzie liczbą liczb pierwszych w zbiorze
będzie liczbą liczb pierwszych w zbiorze 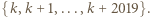 Wśród pierwszych 2020 liczb całkowitych dodatnich jest więcej niż 13 liczb pierwszych, zatem
Wśród pierwszych 2020 liczb całkowitych dodatnich jest więcej niż 13 liczb pierwszych, zatem 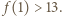 Zauważmy także, że wśród liczb
Zauważmy także, że wśród liczb 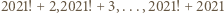 występują same liczby złożone, zatem
występują same liczby złożone, zatem 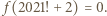 Oczywiście mamy
Oczywiście mamy 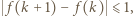 skąd wniosek, że istnieje taka liczba
skąd wniosek, że istnieje taka liczba 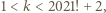 dla której mamy
dla której mamy 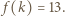 To kończy rozwiązanie zadania.
To kończy rozwiązanie zadania.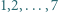 występuje dokładnie raz. Udowodnić, że żadna z tych liczb nie jest dzielnikiem innej.
występuje dokładnie raz. Udowodnić, że żadna z tych liczb nie jest dzielnikiem innej.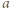 i
i 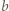 spośród danych w zadaniu. Mamy
spośród danych w zadaniu. Mamy 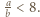 Jeśli
Jeśli 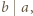 to niech
to niech 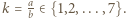 Wówczas
Wówczas 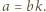 Teraz trzeba zauważyć, że liczby
Teraz trzeba zauważyć, że liczby 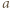 i
i 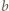 dają resztę 1 z dzielenia przez 9, co wymusza
dają resztę 1 z dzielenia przez 9, co wymusza 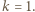
 nie występuje żadna z cyfr 1, 2, 9. Udowodnić, że w zapisie dziesiętnym liczby
nie występuje żadna z cyfr 1, 2, 9. Udowodnić, że w zapisie dziesiętnym liczby 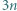 występuje co najmniej jedna z tych cyfr.
występuje co najmniej jedna z tych cyfr.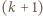 -cyfrowa. Możemy zapisać
-cyfrowa. Możemy zapisać 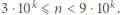 Wystarczy teraz wykazać, że jeśli liczba
Wystarczy teraz wykazać, że jeśli liczba 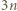 ma tyle samo cyfr co
ma tyle samo cyfr co 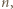 to jej pierwszą cyfrą jest 9, a jeśli ma o jedną cyfrę więcej, to jej pierwszą cyfrą jest 1 lub 2.
to jej pierwszą cyfrą jest 9, a jeśli ma o jedną cyfrę więcej, to jej pierwszą cyfrą jest 1 lub 2.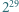 jest dziewięć cyfr, każda inna. Wiedząc to, bez obliczania
jest dziewięć cyfr, każda inna. Wiedząc to, bez obliczania 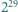 wyznaczyć cyfrę, która w tej liczbie nie występuje.
wyznaczyć cyfrę, która w tej liczbie nie występuje.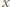 jest brakującą cyfrą, to suma cyfr liczby
jest brakującą cyfrą, to suma cyfr liczby 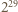 wynosi
wynosi 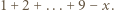 Zauważmy, że liczba
Zauważmy, że liczba 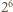 daje resztę 1 z dzielenia przez 9, więc liczba
daje resztę 1 z dzielenia przez 9, więc liczba 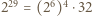 daje resztę 5 z dzielenia przez 9. Wystarczy porównać obie reszty.
daje resztę 5 z dzielenia przez 9. Wystarczy porównać obie reszty.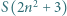 nie jest kwadratem liczby całkowitej dla żadnego naturalnego
nie jest kwadratem liczby całkowitej dla żadnego naturalnego 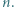
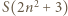 daje taką samą resztę z dzielenia przez 9, co
daje taką samą resztę z dzielenia przez 9, co 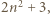 czyli 2, 3, 5 lub 8.
czyli 2, 3, 5 lub 8.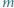 i
i 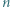 zachodzi nierówność
zachodzi nierówność 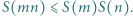
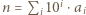 i
i 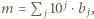 otrzymamy
otrzymamy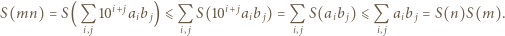
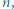 które spełniają równość
które spełniają równość 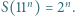
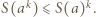 Wobec tego dla
Wobec tego dla 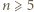 zachodzą nierówności
zachodzą nierówności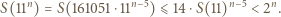
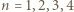 mamy
mamy 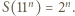
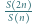 dla całkowitych dodatnich
dla całkowitych dodatnich 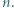

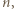 dla których osiągane są skrajne wartości.
dla których osiągane są skrajne wartości.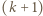 -cyfrową
-cyfrową 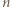 o pierwszej cyfrze
o pierwszej cyfrze 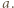 Iloczyn cyfr liczby
Iloczyn cyfr liczby 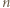 nie przekracza
nie przekracza 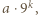 natomiast
natomiast 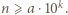 Taka liczba nie istnieje.
Taka liczba nie istnieje. liczby
liczby 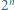 i
i 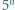 mają taką samą pierwszą cyfrę. Wykazać, że tą cyfrą jest 3.
mają taką samą pierwszą cyfrę. Wykazać, że tą cyfrą jest 3. będzie pierwszą cyfrą
będzie pierwszą cyfrą 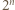 i
i 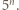 Zapiszmy
Zapiszmy 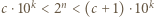 oraz
oraz 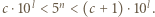 Mnożąc te dwie nierówności, otrzymamy
Mnożąc te dwie nierówności, otrzymamy 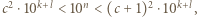 z czego wnioskujemy, że
z czego wnioskujemy, że 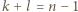 i w konsekwencji
i w konsekwencji 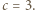
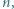 dla których
dla których 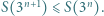
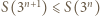 zachodzi tylko dla skończenie wielu
zachodzi tylko dla skończenie wielu 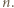 Wtedy istnieje takie
Wtedy istnieje takie 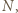 że dla wszystkich
że dla wszystkich 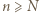 mamy
mamy 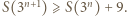 Stąd dla wszystkich
Stąd dla wszystkich 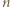 zachodzi nierówność
zachodzi nierówność 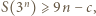 gdzie
gdzie  jest pewną stałą. Z drugiej strony,
jest pewną stałą. Z drugiej strony, 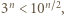 więc liczba
więc liczba 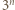 ma co najwyżej
ma co najwyżej 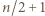 cyfr.
cyfr.