Funkcja Eulera»Zadanie 3
o zadaniu...
- Zadanie pochodzi z artykułu Funkcja Eulera
- Publikacja w Delcie: październik 2019
- Publikacja elektroniczna: 30 września 2019
- Artykuł źródłowy w wersji do druku [application/pdf]: (368 KB)
Wyznaczyć największą liczbę naturalną, która jest wspólnym dzielnikiem liczb 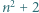 oraz
oraz 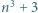 dla pewnej liczby naturalnej
dla pewnej liczby naturalnej 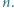
Zadanie 786 zaproponował pan Witold Bednarek z Łodzi.
Dowieść, że istnieje nieskończenie wiele czwórek różnych liczb naturalnych 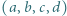 o tej własności, że każdy z iloczynów
o tej własności, że każdy z iloczynów 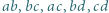 jest o 1 większy od kwadratu pewnej liczby naturalnej.
jest o 1 większy od kwadratu pewnej liczby naturalnej.
Dana jest liczba całkowita 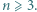 Każdy bok i każdą przekątną
Każdy bok i każdą przekątną 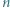 -kąta foremnego pomalowano przy użyciu jednego z
-kąta foremnego pomalowano przy użyciu jednego z  kolorów w taki sposób, że dla każdej trójki kolorów istnieje trójkąt o bokach w tych właśnie kolorach wyznaczony przez trzy spośród wierzchołków danego
kolorów w taki sposób, że dla każdej trójki kolorów istnieje trójkąt o bokach w tych właśnie kolorach wyznaczony przez trzy spośród wierzchołków danego 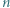 -kąta. Wykazać, że
-kąta. Wykazać, że 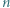 jest liczbą nieparzystą.
jest liczbą nieparzystą.
Dana jest liczba nieparzysta 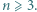 Każdy bok i każdą przekątną
Każdy bok i każdą przekątną 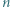 -kąta foremnego pomalowano przy użyciu jednego z
-kąta foremnego pomalowano przy użyciu jednego z  kolorów w taki sposób, że dwa odcinki mają ten sam kolor dokładnie wtedy, gdy są równoległe. Wykazać, że dla każdej trójki kolorów istnieje trójkąt o bokach w tych właśnie kolorach wyznaczony przez trzy spośród wierzchołków danego
kolorów w taki sposób, że dwa odcinki mają ten sam kolor dokładnie wtedy, gdy są równoległe. Wykazać, że dla każdej trójki kolorów istnieje trójkąt o bokach w tych właśnie kolorach wyznaczony przez trzy spośród wierzchołków danego 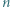 -kąta.
-kąta.
Dany jest wielomian 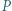 o współczynnikach całkowitych oraz względnie pierwsze dodatnie liczby całkowite
o współczynnikach całkowitych oraz względnie pierwsze dodatnie liczby całkowite 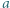 i
i 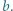 Udowodnić, że jeśli
Udowodnić, że jeśli 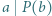 oraz
oraz 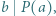 to
to 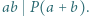
Czy w wyrażeniu 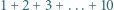 można zamienić niektóre znaki "
można zamienić niektóre znaki " 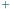 " na "
" na "  " w ten sposób, by wynik był równy
" w ten sposób, by wynik był równy 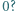
Na tablicy napisano 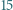 trzycyfrowych liczb pierwszych. Możemy zmazać dwie zapisane na tablicy liczby i zamiast nich zapisać wartość bezwzględną ich różnicy. Postępujemy tak aż do momentu, gdy na tablicy pozostanie jedna liczba. Czy tą liczbą może być
trzycyfrowych liczb pierwszych. Możemy zmazać dwie zapisane na tablicy liczby i zamiast nich zapisać wartość bezwzględną ich różnicy. Postępujemy tak aż do momentu, gdy na tablicy pozostanie jedna liczba. Czy tą liczbą może być 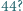
W kręgu stoi 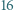 drzew, na każdym siedzi jeden wróbel. Wróble przelatują czasem na inne drzewa, ale zgodnie z regułą: dwa wróble lecą jednocześnie, każdy na drzewo sąsiadujące z tym, na którym siedział, jeden zgodnie, a drugi przeciwnie do ruchu wskazówek zegara. Czy jest możliwe, aby w pewnej chwili wszystkie wróble siedziały na tym samym drzewie?
drzew, na każdym siedzi jeden wróbel. Wróble przelatują czasem na inne drzewa, ale zgodnie z regułą: dwa wróble lecą jednocześnie, każdy na drzewo sąsiadujące z tym, na którym siedział, jeden zgodnie, a drugi przeciwnie do ruchu wskazówek zegara. Czy jest możliwe, aby w pewnej chwili wszystkie wróble siedziały na tym samym drzewie?
Jedno dziecko ma 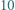 cukierków, drugie
cukierków, drugie 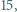 a trzecie
a trzecie 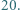 Każde z nich może w dowolnej chwili dać po jednym swoim cukierku pozostałej dwójce. Czy dzieląc się w ten sposób, dzieci mogą doprowadzić do tego, by każde z nich miało
Każde z nich może w dowolnej chwili dać po jednym swoim cukierku pozostałej dwójce. Czy dzieląc się w ten sposób, dzieci mogą doprowadzić do tego, by każde z nich miało 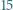 cukierków?
cukierków?
Na polu A1 szachownicy  napisano liczbę 1, na A8 napisano -1, a na pozostałych polach 0. Możemy wielokrotnie wykonywać następującą operację: wybieramy dowolne pole i zmniejszamy napisaną na nim liczbę o liczbę pól sąsiednich (mających wspólny bok), zaś każdą z liczb napisanych na polach sąsiednich zwiększamy o 1. Rozstrzygnąć, czy można doprowadzić do stanu, w którym na wszystkich polach szachownicy napisana jest liczba 0.
napisano liczbę 1, na A8 napisano -1, a na pozostałych polach 0. Możemy wielokrotnie wykonywać następującą operację: wybieramy dowolne pole i zmniejszamy napisaną na nim liczbę o liczbę pól sąsiednich (mających wspólny bok), zaś każdą z liczb napisanych na polach sąsiednich zwiększamy o 1. Rozstrzygnąć, czy można doprowadzić do stanu, w którym na wszystkich polach szachownicy napisana jest liczba 0.
Płaszczyznę podzielono na trójkąty równoboczne w ten sposób, że w każdym wierzchołku (węźle) spotyka się sześć trójkątów. W każdym węźle znajduje się lampka, natomiast na każdym trójkącie jest włącznik, który zmienia stan lampek (świeci albo nie świeci) znajdujących się w węzłach będących wierzchołkami tego trójkąta. Rozstrzygnąć, czy zaczynając od sytuacji, w której świeci się dokładnie jedna lampka, możemy doprowadzić do zgaszenia wszystkich lampek.
Każdą liczbę naturalną pomalowano pewnym kolorem w taki sposób, że jeśli 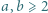 są liczbami naturalnymi, to liczby
są liczbami naturalnymi, to liczby 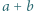 i
i 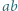 mają ten sam kolor. Dowieść, że wszystkie liczby naturalne większe od
mają ten sam kolor. Dowieść, że wszystkie liczby naturalne większe od 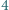 mają ten sam kolor.
mają ten sam kolor.
Niech 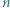 będzie liczbą naturalną. Udowodnić przez indukcję, że:
będzie liczbą naturalną. Udowodnić przez indukcję, że:
(a) 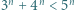 dla
dla 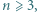 (b)
(b) 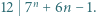
Udowodnić nierówność Bernoulliego: 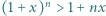 dla wszystkich liczb rzeczywistych
dla wszystkich liczb rzeczywistych 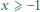 i liczb naturalnych
i liczb naturalnych 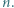
Wiadomo, że 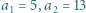 oraz
oraz 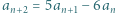 dla
dla 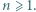 Wykazać, że
Wykazać, że 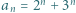 dla wszystkich naturalnych
dla wszystkich naturalnych 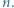
Udowodnić małe twierdzenie Fermata: 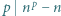 dla każdej liczby pierwszej
dla każdej liczby pierwszej 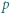 i liczby naturalnej
i liczby naturalnej 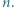
Niech 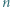 będzie liczbą naturalną. Dowieść, że istnieje
będzie liczbą naturalną. Dowieść, że istnieje  -cyfrowa wielokrotność liczby
-cyfrowa wielokrotność liczby 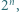 w której zapisie dziesiętnym występują tylko cyfry
w której zapisie dziesiętnym występują tylko cyfry 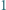 i
i 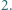
Na stole leży 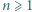 stosów monet, po jednej w każdym. W danej chwili możemy połączyć dwa dowolnie wybrane stosy w jeden. Jeśli połączymy stos
stosów monet, po jednej w każdym. W danej chwili możemy połączyć dwa dowolnie wybrane stosy w jeden. Jeśli połączymy stos 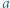 monet ze stosem
monet ze stosem 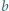 monet, to zapisujemy iloczyn
monet, to zapisujemy iloczyn 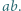 Te czynności wykonujemy aż do uzyskania jednego stosu
Te czynności wykonujemy aż do uzyskania jednego stosu 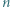 monet. Dowieść, że suma zapisanych iloczynów wynosi
monet. Dowieść, że suma zapisanych iloczynów wynosi 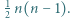
Zadanie 784 zaproponował pan Tomasz Ordowski.
Wyznaczyć wszystkie liczby pierwsze 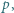 które można zapisać w postaci sumy
które można zapisać w postaci sumy 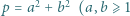 całkowite) tak, by liczba
całkowite) tak, by liczba 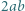 była kwadratem liczby całkowitej.
była kwadratem liczby całkowitej.