Dlaczego niektóre łamigłówki są tak trudne?
Inspiracją do napisania tego artykułu jest znana, popularna i - do czego chcę Czytelnika przekonać - całkiem niełatwa łamigłówka zwana Sudoku. Problem polega na uzupełnieniu częściowo wypełnionej planszy 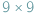 w taki sposób, żeby każdy wiersz i każda kolumna oraz każdy z 9 tzw. regionów
w taki sposób, żeby każdy wiersz i każda kolumna oraz każdy z 9 tzw. regionów 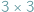 zawierał wszystkie cyfry od 1 do 9. Czy nie przypomina to pewnego innego równie znanego problemu natury kombinatorycznej? Tak, to problem Uzupełniania Kwadratów Łacińskich, których wynalazcą był Leonhard Euler. Być może zainspirował innych, by w przyszłości stworzyli Sudoku...
zawierał wszystkie cyfry od 1 do 9. Czy nie przypomina to pewnego innego równie znanego problemu natury kombinatorycznej? Tak, to problem Uzupełniania Kwadratów Łacińskich, których wynalazcą był Leonhard Euler. Być może zainspirował innych, by w przyszłości stworzyli Sudoku...

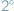 od ekliptyki, co oznacza, że do zaćmień nie dojdzie. Srebrny Glob, przemierzając niebo w swoim cyklu miesięcznym, zacznie miesiąc po I kwadrze, 6 września przejdzie przez pełnię, 13 września - przez ostatnią kwadrę, 20 września - przez nów i 28 września przez I kwadrę. Po drodze minie sporo jasnych gwiazd i planet, z których kilka zakryje (w tym planety Merkury, Wenus, Mars i Neptun oraz gwiazdy Aldebaran i Regulus).
od ekliptyki, co oznacza, że do zaćmień nie dojdzie. Srebrny Glob, przemierzając niebo w swoim cyklu miesięcznym, zacznie miesiąc po I kwadrze, 6 września przejdzie przez pełnię, 13 września - przez ostatnią kwadrę, 20 września - przez nów i 28 września przez I kwadrę. Po drodze minie sporo jasnych gwiazd i planet, z których kilka zakryje (w tym planety Merkury, Wenus, Mars i Neptun oraz gwiazdy Aldebaran i Regulus).
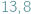 godzin). Został odkryty stosunkowo niedawno, dopiero w 1990 roku, przez Marka R. Showaltera na podstawie analizy zdjęć sondy Voyager 2 w przerwie Enckego pierścienia A Saturna, zebranych na początku lat 80. XX wieku.
godzin). Został odkryty stosunkowo niedawno, dopiero w 1990 roku, przez Marka R. Showaltera na podstawie analizy zdjęć sondy Voyager 2 w przerwie Enckego pierścienia A Saturna, zebranych na początku lat 80. XX wieku.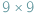 w taki sposób, żeby każdy wiersz i każda kolumna oraz każdy z 9 tzw. regionów
w taki sposób, żeby każdy wiersz i każda kolumna oraz każdy z 9 tzw. regionów 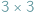 zawierał wszystkie cyfry od 1 do 9. Czy nie przypomina to pewnego innego równie znanego problemu natury kombinatorycznej? Tak, to problem Uzupełniania Kwadratów Łacińskich, których wynalazcą był Leonhard Euler. Być może zainspirował innych, by w przyszłości stworzyli Sudoku...
zawierał wszystkie cyfry od 1 do 9. Czy nie przypomina to pewnego innego równie znanego problemu natury kombinatorycznej? Tak, to problem Uzupełniania Kwadratów Łacińskich, których wynalazcą był Leonhard Euler. Być może zainspirował innych, by w przyszłości stworzyli Sudoku...
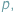 z dodawaniem i mnożeniem modulo
z dodawaniem i mnożeniem modulo 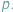 Poniżej przedstawimy trzy klasyczne twierdzenia, których proste dowody są oparte na Combinatorial Nullstellensatz w wersji "resztowej". Twierdzenia te są szczególnie bliskie zastosowaniom olimpijskim.
Poniżej przedstawimy trzy klasyczne twierdzenia, których proste dowody są oparte na Combinatorial Nullstellensatz w wersji "resztowej". Twierdzenia te są szczególnie bliskie zastosowaniom olimpijskim.
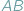 widać z punktu
widać z punktu 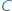 pod kątem
pod kątem 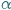 , gdy
, gdy 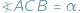 Z twierdzenia o kątach wpisanych wynika, że jeśli punkty
Z twierdzenia o kątach wpisanych wynika, że jeśli punkty 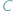 i
i 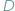 leżą na okręgu po tej samej stronie jego cięciwy
leżą na okręgu po tej samej stronie jego cięciwy 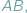 to widać ją z
to widać ją z 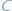 i
i  pod tym samym kątem (
pod tym samym kątem (