Klub 44M - zadania IX 2017»Zadanie 745
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania IX 2017
- Publikacja w Delcie: wrzesień 2017
- Publikacja elektroniczna: 1 września 2017
- Artykuł źródłowy w wersji do druku [application/pdf]: (71 KB)
Na obwodzie trójkąta 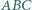 leżą cztery różne punkty
leżą cztery różne punkty 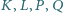 : punkty
: punkty 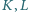 na boku
na boku 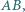 punkty
punkty 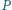 i
i 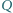 odpowiednio na bokach
odpowiednio na bokach 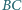 i
i 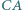 ; przy tym odcinki
; przy tym odcinki 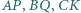 i
i 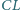 mają jednakową długość. Udowodnić, że środki tych czterech odcinków leżą na jednym okręgu.
mają jednakową długość. Udowodnić, że środki tych czterech odcinków leżą na jednym okręgu.

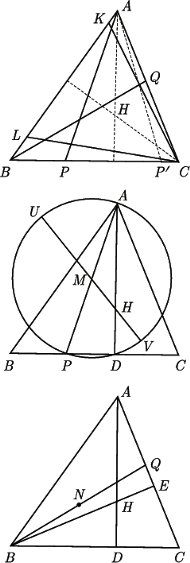
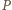 przez
przez 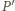 - drugi punkt prostej
- drugi punkt prostej 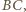 leżący w tej samej odległości od
leżący w tej samej odległości od 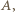 co punkt
co punkt 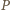 ; zaś środek szukanego okręgu powinien leżeć na osiach symetrii trójkątów równoramiennych
; zaś środek szukanego okręgu powinien leżeć na osiach symetrii trójkątów równoramiennych 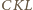 i
i 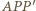 - czyli na wysokościach trójkąta
- czyli na wysokościach trójkąta 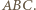 Stąd domysł uściślenia tezy zadania: wykazać, że środki odcinków
Stąd domysł uściślenia tezy zadania: wykazać, że środki odcinków 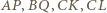 (o jednakowej długości
(o jednakowej długości 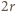 ) leżą na okręgu o środku
) leżą na okręgu o środku 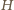 (ortocentrum trójkąta
(ortocentrum trójkąta 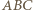 ).
).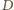 będzie spodkiem wysokości opuszczonej z wierzchołka
będzie spodkiem wysokości opuszczonej z wierzchołka 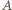 i niech
i niech 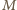 będzie środkiem odcinka
będzie środkiem odcinka 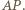 Weźmy pod uwagę okrąg o środku
Weźmy pod uwagę okrąg o środku 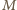 i promieniu
i promieniu  (czyli o średnicy
(czyli o średnicy 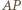 ). Prosta
). Prosta 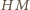 przecina ów okrąg w punktach
przecina ów okrąg w punktach 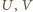 (gdy punkty
(gdy punkty 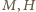 pokrywają się, przyjmijmy
pokrywają się, przyjmijmy 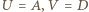 ). Cięciwa
). Cięciwa 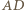 tego okręgu oraz jego średnica
tego okręgu oraz jego średnica 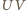 przecinają się w punkcie
przecinają się w punkcie  Zatem
Zatem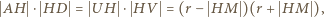
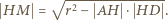
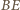 jest drugą wysokością trójkąta
jest drugą wysokością trójkąta 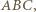 a
a 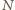 jest środkiem odcinka
jest środkiem odcinka 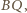 to analogicznie uzyskujemy równość
to analogicznie uzyskujemy równość
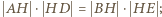 wynika to z podobieństwa trójkątów
wynika to z podobieństwa trójkątów 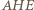 i
i 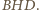 Tak więc
Tak więc 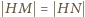 ; środki odcinków
; środki odcinków 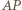 i
i 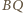 leżą w jednakowej odległości od punktu
leżą w jednakowej odległości od punktu 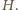 Analogicznie, w tej samej odległości od
Analogicznie, w tej samej odległości od 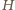 leżą też środki odcinków
leżą też środki odcinków 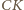 i
i 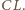 To właśnie nasza teza.
To właśnie nasza teza.