Rozważmy dowolny podział zbioru dodatnich liczb całkowitych spełniający zadane warunki. Zauważmy, że jeżeli 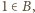 to dla dowolnego
to dla dowolnego 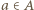 mamy
mamy 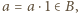 co jest sprzeczne z założeniem, że zbiory
co jest sprzeczne z założeniem, że zbiory 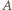 i
i 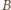 są rozłączne. Wobec tego
są rozłączne. Wobec tego 
Oznaczmy przez 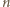 najmniejszy element zbioru
najmniejszy element zbioru 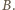 Korzystając z pierwszego z danych warunków, łatwo indukcyjnie udowodnić, że dla każdej dodatniej liczby całkowitej
Korzystając z pierwszego z danych warunków, łatwo indukcyjnie udowodnić, że dla każdej dodatniej liczby całkowitej 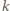 :
:
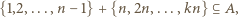
skąd wniosek, że wszystkie liczby niepodzielne przez 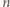 należą do zbioru
należą do zbioru 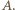 W szczególności z drugiego z danych warunków wynika, że każda liczba podzielna przez
W szczególności z drugiego z danych warunków wynika, że każda liczba podzielna przez 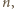 ale niepodzielna przez
ale niepodzielna przez 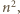 należy do zbioru
należy do zbioru 
Przypuśćmy, że 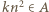 dla pewnej dodatniej liczby całkowitej
dla pewnej dodatniej liczby całkowitej 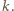 Wówczas, skoro
Wówczas, skoro 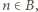 to
to 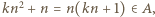 co jest sprzeczne z konkluzją poprzedniego akapitu. To oznacza, że wszystkie liczby podzielne przez
co jest sprzeczne z konkluzją poprzedniego akapitu. To oznacza, że wszystkie liczby podzielne przez 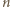 należą do zbioru
należą do zbioru 
Pozostaje zauważyć, że dla każdego 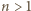 jeżeli
jeżeli 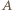 jest zbiorem liczb niepodzielnych przez
jest zbiorem liczb niepodzielnych przez 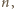 a
a 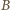 - zbiorem liczb podzielnych przez
- zbiorem liczb podzielnych przez 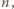 to warunki zadania są spełnione.
to warunki zadania są spełnione.
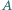 i
i 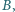 że
że