Obserwacje planet pozasłonecznych mają, jak na astronomię, względnie krótką historię. Pierwsze planety poza naszym układem odkryli w 1992 roku Andrzej Wolszczan i Dale Frail, analizując radiowe obserwacje pulsarów (odkrycie nastąpiło przez przypadek, ponieważ nikt nie spodziewał się planet krążących wokół martwej pozostałości po supernowej). Pierwszą planetą związaną z "prawdziwą" gwiazdą (i to gwiazdą Ciągu Głównego) jest 51 Pegasi...

Kilka nocy po pełni Księżyca, wypadającej 11 IV, warto wykonać obserwacje gromady kulistej M3, zwanej również NGC 5272. Gromada ta odkryta została w 1794 roku i przyczyniła się do podjęcia przez Messiera decyzji o stworzeniu katalogu obiektów mgławicowych.

Ten okrzyk często rozlega się na lekcjach fizyki. Czy warto sprawdzać wymiary? Przecież na lekcjach matematyki, gdzie też rozwiązuje się mnóstwo zadań, czegoś takiego się nie robi. Otóż warto. Z kilku powodów. W fizyce mamy do czynienia z wieloma wielkościami fizycznymi, mierzonymi w różnych jednostkach. Nie można porównywać wielkości mierzonych w różnych jednostkach, tak jak nie można porównywać jabłek i gruszek.

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

Sprawdzanie poprawności dowodów matematycznych często wymaga sporej wiedzy i ogromu nużącej pracy. O ile dochodzenie do zrozumienia istoty dowodu, czyli dlaczego dane twierdzenie matematyczne zachodzi, może sprawiać Czytelnikowi dużo satysfakcji, o tyle weryfikowanie wszystkich szczegółów dowodu jest zajęciem dość niewdzięcznym. Z tego powodu od wielu już lat trwają badania nad zaprzęgnięciem komputerów do tej żmudnej części pracy...

W informatyce losowość jest bardzo przydatna. Często bardzo ułatwia rozumowania, pozwala na piękne i klarowne argumenty używające, na przykład, metody probabilistycznej. Nieraz łatwo znaleźć algorytm używający losowości (randomizowany) i działający szybko, podczas gdy znalezienie szybkiego algorytmu deterministycznego jest trudne lub w ogóle takiego nie znamy. Z losowością jest jednak pewien problem...

W tym odcinku prezentujemy najtrudniejsze zadanie z zeszłorocznej Międzynarodowej Olimpiady Informatycznej.

Tak zwany Problem Stopu to problem decyzyjny, którego wejściem jest jakiś program 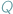i jakieś dane 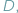a którego rozwiązaniem (wyjściem) jest stwierdzenie, czy program 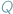uruchomiony na danych 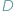zakończy swoje działania w skończonym czasie.

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

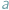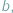Udowodnijmy lub obalmy twierdzenie: istnieją takie liczby niewymierne i że 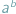jest liczbą wymierną.

Paradoks Banacha-Tarskiego (1924 r.). Kulę można rozłożyć na skończenie wiele części, z których da się zbudować dwie takie same kule.

Tym razem będziemy wycinać...

Twierdzenie Talesa dowieść można bez trudu...

Twierdzenie Pascala o równomiernym ciśnieniu gazu na ścianki naczynia pociąga za sobą twierdzenie Pitagorasa i jego uogólnienie, czyli twierdzenie kosinusów.

W tym artykule chcemy zaprezentować pewną technikę dowodową zwaną interpretacją kombinatoryczną. Metoda ta pokazana będzie w działaniu: podajemy dwa zadania wraz z rozwiązaniami, które są ilustracją tematu.

Naszą wiedzę o zjawiskach lub przedmiotach wygodnie jest zapisywać w postaci koniunkcji wyrażanej za pomocą spójnika "i" (np. w ten sposób można powiedzieć, że kaczki mają skrzydła i latają). Niestety, taki format nie sprawdza się dobrze...

Metoda probabilistyczna gościła już na łamach Delty (np. w numerach 12/2006 i 4/2015), byłoby jednak nieprawdopodobnie głupio pominąć ją w numerze poświęconym dowodom.

Małe Twierdzenie Fermata ma również taki dowód...

Zbiór wszystkich liczb rzeczywistych 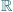nie jest równoliczny ze zbiorem wszystkich liczb naturalnych

Indukcja pozaskończona wykorzystywana jest w dowodach istnienia różnych obiektów matematycznych. Główną częścią tego typu dowodu jest definicja indukcyjna (inaczej: rekurencyjna) funkcji.

Tym, co czyni matematyków pewnymi swoich racji, jest dowód - niepoddające się żadnym wątpliwościom uzasadnienie głoszonych stwierdzeń (Kartezjusz: jedni tylko matematycy zdołali znaleźć jakieś dowody, to znaczy jakieś racje pewne i oczywiste).

Kilka kolejnych spotkań w Centrum Nauki Kopernik pod wspólnym tytułem "Drogi do życia" poświęcono konfrontacjom współczesnych nauk molekularnych w zakresie biologii z postępami medycyny w dość węzłowych kwestiach: nowotwory, krew i odporność, szczepienia ochronne i antybiotyki, genetyczne podstawy chorób, w tym neurologicznych, i wreszcie perspektywy leczenia i regeneracji rdzenia kręgowego. Przywołując pamięć o tych spotkaniach, czuję, że dotknięto naprawdę ważnych zagadnień, szczegółów różnorodnych rozwiązań. Mówiono także o nadziei.

Sławny problem "ile diabłów mieści się na ostrzu szpilki" istotnie bywał rozpatrywany, z tym że takie sformułowanie problemu jest już dziełem renesansowych prześmiewców. Poważnie problem ten rozpatrywał Tomasz z Akwinu w Summa Theologiae, część II (O aniołach), rozdział LII §3: Czy wielu aniołów może być równocześnie w tem samem miejscu?