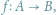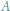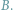Delta mi!

W poprzednim odcinku zastanawialiśmy się, czy istnieje "nieskończoność" pomiędzy licznością zbioru liczb naturalnych i licznością zbioru liczb rzeczywistych. Pora na ostatni etap naszej podróży. Będzie to etap jeszcze dalej prowadzący w nieskończoność - będziemy rozważać i konstruować coraz większe "nieskończoności". Okaże się, że jest ich bardzo nieskończenie wiele. Może aż za bardzo.

W tym odcinku zajmiemy się hipotezą continuum.

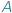W poprzedniej części tej opowieści o nieskończonościach rozważaliśmy twierdzenie Cantora, które stanowi, że żaden zbiór nie jest równoliczny ze zbiorem jego podzbiorów 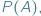co symbolicznie notujemy 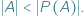Szczególnie zajmowaliśmy się przypadkiem, gdy 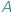jest zbiorem liczb naturalnych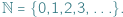

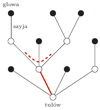
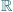W zeszłym roku (już po raz drugi!) miałem przyjemność pełnić funkcję tutora podczas obozu Maths Beyond Limits. Poprowadziłem dwie serie zajęć, z których jedna dotyczyła teorii mnogości. Starając się dać uczestnikom podstawy arytmetyki zbiorów nieskończonych w zajmujący i bezbolesny, mam nadzieję, sposób, pokazałem ciekawe zadania, wykorzystujące różne metody i pomysły. Jeden z nich jest szczególnie warty uwagi...

W poprzednim odcinku sprawdziliśmy, że zbiór liczb naturalnych jest równoliczny ze zbiorem liczb wymiernych (także zbiór liczb całkowitych jest równoliczny z każdym z nich). Inaczej mówiąc, można ustawić liczby wymierne w pary z liczbami naturalnymi w taki sposób, że każda liczba wymierna stoi w parze z dokładnie jedną liczbą naturalną i każda liczba naturalna stoi w parze z dokładnie jedną liczbą wymierną. Można też powiedzieć, że wszystkie liczby wymierne da się zakwaterować w hotelu Hilberta.

Kontynuując naszą przygodę z nieskończonością, spróbujmy wypracować podstawowe narzędzia do jej badania. Przyda nam się w tym celu pewna analogia pomiędzy zbiorami nieskończonymi a tymi skończonymi. Wyobraźmy sobie dwa skończone zbiory osób. Powiedzmy, że elementami pierwszego z nich są: Aldona, Balbina, Cezaria oraz Delfina, a elementami drugiego: Abelard, Baldwin, Cyryl oraz Dezyderiusz. Od razu zauważamy, że te zbiory mają tyle samo elementów. Jak dojść do tego wniosku? Można policzyć elementy w każdym ze zbiorów i w obu przypadkach wyjdzie cztery. A co by było, gdybyśmy nie umieli liczyć do czterech? Czy jest inna metoda pozwalająca na stwierdzenie, że te zbiory mają tyle samo elementów?

Zbiór to najbardziej podstawowe pojęcie matematyki. Ze zbiorami mamy do czynienia właściwie we wszystkich dyscyplinach matematycznych. Choć każdy Czytelnik na pewno intuicyjnie rozumie słowo "zbiór" (np. jako kolekcję lub zestaw utworzony z pewnego rodzaju elementów), to pojęcie to nie ma formalnej definicji.

Biorąc dwa skończone zbiory, można na dwa sposoby sprawdzić, że mają tyle samo elementów. Albo policzyć elementy w każdym z nich, albo też ustawić w pary elementy pierwszego zbioru z elementami drugiego.

Na nieskończoność natrafiono już w starożytności. Nic dziwnego, że była traktowana z podejrzliwością, w końcu wszystko w prawdziwym świecie wydawało się skończone. Bywała źródłem problemów, paradoksów i sporów (na przykład, paradoks Zenona z Elei). W końcu, w drugiej połowie XIX wieku, nieskończoność udało się nieco oswoić (nie mylić z ujarzmić), weszła do kanonu matematyki, a właściwie w jej fundamenty. Owo oswajanie zaczęło się od Georga Cantora...

Nieskończoność... Co myślisz, gdy słyszysz to słowo? Może myślisz o rozgwieżdżonym niebie? Może próbujesz wyobrazić sobie coś bardzo, ale to bardzo dużego? A może myślisz o ludzkiej wyobraźni i sile naszego umysłu? George Cantor postanowił potraktować nieskończoność jak coś "zwykłego" i po prostu ją zbadał. Pójdziemy jego śladem. Zastanówmy się... Czy każda nieskończoność jest taka sama? Czy też może są większe i mniejsze? Czy wszechświat jest nieskończony? Co to jest nieskończoność? Na wiele pytań dotyczących nieskończoności udzielono wyczerpujących odpowiedzi. Na część z nich odpowiedzi nie są znane. O niektórych wiadomo, że nie da się na nie odpowiedzieć po prostu "tak" lub "nie".

Drodzy Poszukiwacze Przygód, witam Was na kolejnym szkoleniu. Dzisiaj nauczymy się jak rozpoznawać, znajdować i radzić sobie w boju z Hydrą. Hydry to paskudne stworzenia, zamieszkujące świat grafów. Niech Was nie zmyli rysunek obok. Zobaczcie, jak przerażająco on wygląda. Hydry to bestie, które tylko upodobniają się do drzew, aby Was zmylić! Tam, gdzie niektórzy z Was dostrzegają korzeń, znajduje się tułów bestii. Tam, gdzie wydają się być liście, są głowy naszego stwora. Krawędzie to szyje, a wierzchołki wewnętrzne to zgięcia.

Indukcja pozaskończona wykorzystywana jest w dowodach istnienia różnych obiektów matematycznych. Główną częścią tego typu dowodu jest definicja indukcyjna (inaczej: rekurencyjna) funkcji.

Zbiór wszystkich liczb rzeczywistych nie jest równoliczny ze zbiorem wszystkich liczb naturalnych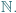

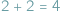Słyszy się często: "to pewne, jak ". Zdania matematyczne bywają podawane za wzór niewzruszonej i absolutnej prawdy. Pytanie, jakie zdania? Niewątpliwie pewniki, czyli aksjomaty ("przez dwa punkty przechodzi dokładnie jedna prosta") oraz twierdzenia, choćby tak łatwe, jak to zacytowane na początku.

Każda nauka ścisła ma własne metody potwierdzania swoich tez. Dla większości z nich weryfikacja twierdzeń polega na konfrontacji z rzeczywistością. Matematyka jest jedyną z tych nauk, w której owa rzeczywistość nie jest ostateczną (ani jakąkolwiek) metodą sprawdzania zdań aspirujących do wzbogacenia zasobu wiedzy matematycznej. Weryfikatorem twierdzeń jest dowód. Mowa tu o tzw. matematyce czystej lub teoretycznej; zauważmy jednak, że fizyczna rzeczywistość weryfikuje stosowalność instrumentów matematycznych, nie ich wartość matematyczną.

W deltoidzie 7/2013 wykazaliśmy, że odcinek nie jest przeliczalny, posługując się tzw. metodą przekątniową Cantora. Tym razem udowodnimy ten sam fakt, wykorzystując pewną dwuosobową grę, której „planszą” jest zbiór 

Czy nieskończoność jest tylko jedna? Nie, istnieją różne, większe i mniejsze!

Często pojawiające się w matematyce zadanie polega na skonstruowaniu funkcji  spełniającej pewne warunki. Między innymi możemy chcieć, aby funkcja ta była różnowartościowa i „na”, co gdyby miało miejsce, oznaczałoby równoliczność zbiorów i  Punktem wyjścia bywa inna funkcja  która potrzebnych warunków nie spełnia, ale wystarczy ją tylko trochę zmienić.

Cóż prostszego, jak stworzyć zbiór z dowolnych prawdziwych lub wymyślonych obiektów! Czyż zbiór nie jest po prostu pewną konstrukcją myślową? Wystarczy zatem pomyśleć o owych obiektach jako o elementach jednego zbioru – i już.

W tym artykule zajmiemy się nieco dokładniej diagramami Venna.

Moja rodzina lubi pizzę, a ja lubię ją piec. Jednak w naszej gromadce nikt nie lubi jeść takiej samej pizzy, jak pozostali członkowie rodziny. Jest nas tylko czworo, więc można sobie z tym poradzić bez trudu, używając tylko dwóch składników – typowa pizza wygląda więc tak...

Jednym z podstawowych sposobów mierzenia zbioru jest liczenie jego elementów. Liczenie ma jednak jasny sens tylko dla zbiorów skończonych. Wiadomo, co to znaczy, że jakiś zbiór ma czy elementów. W przypadku zbiorów nieskończonych sytuacja jest natomiast znacznie mniej oczywista. Czy zbiorowi nieskończonemu da się w ogóle przypisać liczbę elementów sensowniej niż przez uznanie, że wynosi ona zawsze ?