Delta mi!

Wbrew pozorom tytuł niniejszego tekstu nie jest efektem zestawienia dwóch przypadkowych słów; nawet zupełnie przypadkowe przypadki mogą zdradzać pewne regularności i fakt ten wcale ich przypadkowości nie przeczy. Przypadkiem ich praktycznego zastosowania są średniowieczne tablice do gry w kości; opisane w nich zasady faworyzują jedną ze stron w sposób na tyle delikatny, że oszukiwana strona wcale się taką nie czuje...

Powiada Ewangelia: Łatwiej jest wielbłądowi przejść przez ucho igielne, niż bogatemu wejść do królestwa niebieskiego.

Na stole leżą, ułożone w losowej kolejności koszulkami do góry, trzy karty: As, Król i Dama. Jeżeli gracz odgadnie prawidłowo położenie Asa, wygrywa dużą nagrodę. Gracz wskazał kartę, nie obejrzał jej, i wtedy prowadzący grę mówi: Chwileczkę. Odkryję jedną z dwóch pozostałych kart, a ty się zastanów, czy chcesz zmienić swoją kartę na kartę, która pozostała nieodkryta.

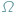W teorii prawdopodobieństwa mówimy o modelu klasycznym, gdy zbiór wszystkich zdarzeń elementarnych jest zbiorem skończonym i wszystkie zdarzenia jednoelementowe są jednakowo prawdopodobne...

Są trzy symetryczne monety...

Filozof może się zadowolić tym, że "wie, że nic nie wie". Fizyk zaś potrzebuje wiedzieć, ile nie wie...

Zwykła moneta często okazuje się doskonałym narzędziem do rozstrzygania konfliktów. Zapewne każdemu zdarzyło się usłyszeć magiczną formułkę "orzeł to, reszka tamto", z reguły będąc przychylnym dokładnie jednemu ze zdarzeń "to" lub "tamto". Takie rozwiązanie jest jednak mało widowiskowe - o ile wzajemne obrzucanie się inwektywami (w celu wytłumaczenia, w jak wielkim błędzie jest strona przeciwna, prezentując zdanie odmienne od naszego) szybko przyciąga publiczność, tak zakończenie sporu przy użyciu jednego rzutu monetą może pozostawić ją z odczuciem niedosytu.

Wyobraź sobie, Czytelniku, że na skutek wieloletnich ćwiczeń i poznania kilku szulerskich sztuczek udało Ci się zwiększyć swoje szanse na wygraną w grze blackjack do Kuszony wizją bajecznego bogactwa w końcu zdecydowałeś się odwiedzić kasyno, by tam spożytkować swoje niesamowite umiejętności. Z miną zawodowego pokerzysty przysiadłeś się do odpowiedniego stolika i zacząłeś grać...

W pierwszej części cyklu (Delta 2/2015) mieliśmy okazję przyjrzeć się wybranym przykładom zaskakujących połączeń, z którymi możemy spotkać się w świecie matematyki. W drugiej części zapoznamy się z jednym z takich połączeń dużo dokładniej. Mowa tu o metodzie probabilistycznej, wiązanej często z nazwiskiem Paula Erdősa, który w trakcie swojej kariery naukowej korzystał z niej niezliczoną liczbę razy.

W Delcie 1/2015 Łukasz Rajkowski oszacował, kiedy należy spodziewać się końca świata. Narzędziem użytym w tej analizie było wnioskowanie bayesowskie. Nie od dziś wiadomo, że należy je stosować z odpowiednią ostrożnością oraz dbałością o założenia i interpretacje. Dlaczego? Zastanówmy się nad poniższym prostym przykładem, gdzie na użytek tych, którzy nie wyobrażają sobie prawdopodobieństwa bez kul w urnach lub rzutów monetą, został wykorzystany ten ostatni model.

Zderzenie z asteroidą, wojna nuklearna, globalny potop, przebiegunowanie Ziemi... liczba katastrof oznaczających koniec ziemskiej cywilizacji powinna skłonić nas do traktowania każdego spokojnego poranka, kiedy przewracamy się leniwie z boku na bok zamiast skwierczeć w ogniu Apokalipsy, jako prawdziwego cudu. Mnogość śmiercionośnych zagrożeń sprawia, że ludzkość od zamierzchłych czasów stara się przewidzieć datę (choćby przybliżoną) własnego końca, nie przejmując się zbytnio kolejnymi niepowodzeniami w tej materii. Większość z proponowanych terminów pochodziła od astrologów, numerologów lub przywódców religijnych. Zgodnie z powiedzeniem Hugo Steinhausa "Matematyk zrobi to lepiej" spróbujmy zastanowić się, co ma do powiedzenia w kwestii terminu Końca Świata Królowa Nauk.

W artykule Tak bardzo oczekiwana wartość z Delty 9/2014 zajęliśmy się tzw. paradoksem petersburskim, w którym wartość oczekiwana zmiennej losowej jest nieskończona. Paradoks ten można wyjaśnić, odwołując się do intuicji z teorii gier...

Nazywano ją kiedyś nadzieją. Czasami dodawano przymiotnik "matematyczna", żeby nie było nieporozumień. Chodziło bowiem o wartość oczekiwaną, czyli o pojęcie znane z rachunku prawdopodobieństwa. Słowo nadzieja faktycznie budziło wątpliwości, szczególnie gdy mierzono jakieś negatywnie nacechowane wielkości, jak liczba zgonów, wypadków samochodowych czy strat. Powiedzenie "nadzieja, jeśli chodzi o wysokość straty, wynosi 100 zł" brzmi zupełnie inaczej niż "wartość oczekiwana straty to 100 zł".

W pierwszej części artykułu szukaliśmy prawdopodobieństwa tego, że umierający człowiek będzie starszy od wszystkich aktualnie żyjących. Zadanie wykonaliśmy. Obliczyliśmy interesujące nas prawdopodobieństwo. Pozwólmy sobie teraz na kilka komentarzy i dygresji. Przypomnijmy najważniejszy wynik pomocniczy, który udowodniliśmy przed miesiącem.

Wyobraźmy sobie następującą grę. Mamy planszę o polach ponumerowanych od 0 do 100 i dwa pionki, stojące na początku na polu o numerze 0. Gracze wykonują ruchy na przemian. Gracz rzuca monetą i jeśli wypadnie reszka, to przesuwa swój pionek o 1 pole, a jeśli orzeł – o 5 pól. Wygrywa ten, kto pierwszy dojdzie do pola o numerze 100.

czyli co dzieje się z łańcuchami Markowa po długim czasie...

Zacznijmy od prostego przykładu. Pchła skacze między ziemią, kotem i człowiekiem. Za każdym razem wybiera miejsce docelowe z takim samym prawdopodobieństwem (równym ). Mogłaby tak skakać w nieskończoność, gdyby nie to, że po wskoczeniu na człowieka ginie. Ile średnio skoków pchła wykona przed śmiercią, jeżeli zaczyna na ziemi?

Organizatorzy gier liczbowych typu lotto przeznaczają sporą część dochodu na zysk i koszt pozyskania dochodu i ten fakt sprawia, że wiele osób powstrzymuje się od gry, a dopiero mechanizm kumulacji powoduje zainteresowanie grą. Dla organizatorów gier kumulacja jest tylko formą odłożenia wypłaty, przeto nic na niej nie tracą, natomiast nowi grający, oczekujący zysku z podziału kwoty odłożonej, grają przeciw stałym graczom.