Klub 44M - zadania III 2015»Zadanie 697
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania III 2015
- Publikacja w Delcie: marzec 2015
- Publikacja elektroniczna: 1 marca 2015
- Artykuł źródłowy w wersji do druku [application/pdf]: (91 KB)
Dana jest liczba naturalna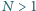 
bezkwadratowa (tj. niepodzielna przez kwadrat żadnej liczby naturalnej większej od 1). Spośród wszystkich dodatnich dzielników liczby 
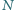losujemy kolejno, bez zwracania, dwa dzielniki: 
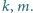Rozważamy zdarzenia:
(A) liczby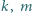 
są względnie pierwsze;
(B) liczba 
jest podzielna przez 
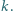
Które z tych zdarzeń jest bardziej prawdopodobne? Czy odpowiedź zmieni się, gdy losowanie będzie wykonywane ze zwracaniem?
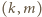dzielników liczby 
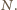Zdarzenia 
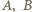identyfikujemy z odpowiednimi podzbiorami zbioru wszystkich takich par. Gdy para 
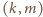należy do 
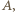liczby 
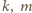są względnie pierwszymi dzielnikami liczby 
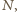zatem także iloczyn 
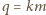jest dzielnikiem 
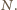Oczywiście 
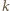dzieli 
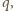więc para 
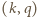należy do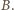 
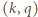jest dowolną parą ze zbioru 
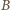(więc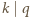 
), wtedy iloraz 
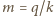też jest dzielnikiem 
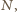i to względnie pierwszym z 
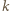(bo gdyby 
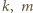miały wspólny dzielnik 
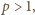liczba 
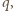więc i 
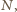byłaby podzielna przez 
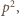wbrew założeniu zadania). Zatem para 
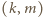należy do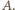 
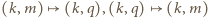są wzajemnie odwrotne. Stąd wynika, że zbiory 
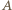i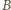 
są równoliczne; zaś zdarzenia 
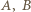są (przy losowaniu ze zwracaniem) jednakowo prawdopodobne.
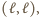gdzie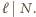 
W poprzednim modelu, do zbioru 
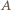należała tylko jedna taka para 
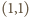; do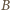 
należały wszystkie. Więcej par zostało wyeliminowanych z 
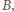wobec czego (przy losowaniu bez zwracania) zdarzenie 
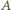jest bardziej prawdopodobne niż 