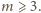Weźmy pod uwagę dowolne rozmieszczenie typu (B). Niech
 będzie
liczbą sąsiadującą w wierszu z liczbą 1; zatem
będzie
liczbą sąsiadującą w wierszu z liczbą 1; zatem
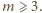 Wykonujemy
następującą operację:
Wykonujemy
następującą operację:
Każdą liczbę
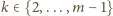 zmniejszamy o 1,
zaś jedynkę zastępujemy przez
zmniejszamy o 1,
zaś jedynkę zastępujemy przez
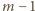 ; pozostałych liczb nie zmieniamy.
(Na ilustracji przykładowe rozmieszczenie typu (B) dla
; pozostałych liczb nie zmieniamy.
(Na ilustracji przykładowe rozmieszczenie typu (B) dla
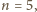 w którym
w którym
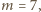 oraz nowe rozmieszczenie, powstałe w wyniku opisanej
operacji).
oraz nowe rozmieszczenie, powstałe w wyniku opisanej
operacji).
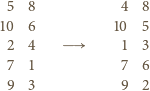
W nowym rozmieszczeniu widzimy wiersz, w którym sąsiadują ze sobą dwie
liczby różniące się o 1, mianowicie
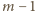 i
i
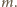 Jest to jedyny taki
wiersz – bowiem w pozostałych wierszach moduł różnicy między oboma
wyrazami albo się zwiększył, albo pozostał niezmieniony. Uzyskaliśmy więc
rozmieszczenie typu (A).
Jest to jedyny taki
wiersz – bowiem w pozostałych wierszach moduł różnicy między oboma
wyrazami albo się zwiększył, albo pozostał niezmieniony. Uzyskaliśmy więc
rozmieszczenie typu (A).
Zauważmy, że widząc uzyskane rozmieszczenie, jesteśmy w stanie
jednoznacznie odtworzyć rozmieszczenie wyjściowe: mamy wiersz z liczbami
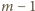 i
i
 ; trzeba zastąpić
; trzeba zastąpić
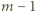 przez jedynkę, zaś każdą
liczbę
przez jedynkę, zaś każdą
liczbę
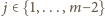 trzeba zwiększyć o 1.
trzeba zwiększyć o 1.
Opisana operacja określa zatem różnowartościową funkcję ze zbioru
rozmieszczeń typu (B) do zbioru rozmieszczeń typu (A). Jednak nie na cały
ów zbiór. Przecież rozmieszczenie typu (A) może mieć w jednym
wierszu liczby 1, 2 (a w pozostałych wierszach pary liczb, różniących się
więcej niż o 1). Natomiast opisana operacja produkuje rozmieszczenia
z pojedynczymi wierszami postaci
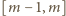 lub
lub
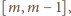 gdzie
gdzie
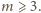
Wniosek: jest więcej rozmieszczeń typu (A); wylosowanie takiego rozmieszczenia
jest bardziej prawdopodobne niż typu (B).
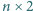 (
(
 wierszy,
2 kolumny,
wierszy,
2 kolumny,
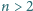 ) wpisujemy liczby od 1 do
) wpisujemy liczby od 1 do
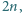 losowo,
z jednakowym prawdopodobieństwem każdego rozmieszczenia. Które
z następujących zdarzeń jest bardziej prawdopodobne?
losowo,
z jednakowym prawdopodobieństwem każdego rozmieszczenia. Które
z następujących zdarzeń jest bardziej prawdopodobne?

 będzie
liczbą sąsiadującą w wierszu z liczbą 1; zatem
będzie
liczbą sąsiadującą w wierszu z liczbą 1; zatem
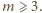 Wykonujemy
następującą operację:
Wykonujemy
następującą operację: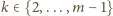 zmniejszamy o 1,
zaś jedynkę zastępujemy przez
zmniejszamy o 1,
zaś jedynkę zastępujemy przez
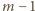 ; pozostałych liczb nie zmieniamy.
(Na ilustracji przykładowe rozmieszczenie typu (B) dla
; pozostałych liczb nie zmieniamy.
(Na ilustracji przykładowe rozmieszczenie typu (B) dla
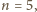 w którym
w którym
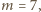 oraz nowe rozmieszczenie, powstałe w wyniku opisanej
operacji).
oraz nowe rozmieszczenie, powstałe w wyniku opisanej
operacji).
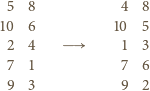
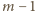 i
i
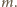 Jest to jedyny taki
wiersz – bowiem w pozostałych wierszach moduł różnicy między oboma
wyrazami albo się zwiększył, albo pozostał niezmieniony. Uzyskaliśmy więc
rozmieszczenie typu (A).
Jest to jedyny taki
wiersz – bowiem w pozostałych wierszach moduł różnicy między oboma
wyrazami albo się zwiększył, albo pozostał niezmieniony. Uzyskaliśmy więc
rozmieszczenie typu (A).
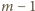 i
i
 ; trzeba zastąpić
; trzeba zastąpić
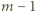 przez jedynkę, zaś każdą
liczbę
przez jedynkę, zaś każdą
liczbę
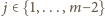 trzeba zwiększyć o 1.
trzeba zwiększyć o 1.
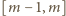 lub
lub
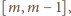 gdzie
gdzie