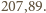Niech
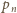 będzie prawdopodobieństwem wylosowania słowa dobrego,
tj. takiego, w którym dwie wyróżnione litery nie sąsiadują, zaś
będzie prawdopodobieństwem wylosowania słowa dobrego,
tj. takiego, w którym dwie wyróżnione litery nie sąsiadują, zaś
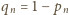 prawdopodobieństwem wylosowania słowa złego. Zapiszmy
te wartości jako sumy
prawdopodobieństwem wylosowania słowa złego. Zapiszmy
te wartości jako sumy
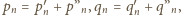 gdzie pojedynczy
prim odpowiada sytuacjom, gdy ostatnia litera słowa jest niewyróżniona,
a podwójny prim – sytuacjom, gdy ostatnia litera jest wyróżniona. Mamy
zależności rekurencyjne
gdzie pojedynczy
prim odpowiada sytuacjom, gdy ostatnia litera słowa jest niewyróżniona,
a podwójny prim – sytuacjom, gdy ostatnia litera jest wyróżniona. Mamy
zależności rekurencyjne
wyjaśnienie ostatniej z nich: złe
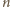 -słowo, zakończone jedną
z wyróżnionych liter, można uzyskać z dowolnego złego
-słowo, zakończone jedną
z wyróżnionych liter, można uzyskać z dowolnego złego
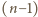 -słowa
(dopisując na końcu jedną z tych dwóch liter), bądź z dobrego
-słowa
(dopisując na końcu jedną z tych dwóch liter), bądź z dobrego
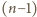 -słowa, zakończonego wyróżnioną literą (dopisując drugą
wyróżnioną literę); uzasadnienie pozostałych zależności jest podobne.
Odejmując dwie ostatnie równości otrzymujemy
-słowa, zakończonego wyróżnioną literą (dopisując drugą
wyróżnioną literę); uzasadnienie pozostałych zależności jest podobne.
Odejmując dwie ostatnie równości otrzymujemy
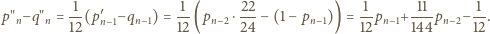
Jednocześnie ta sama różnica daje się zapisać jako
Przyrównanie prawych stron uzyskanych równości daje jednorodną
rekurencję liniową drugiego rzędu
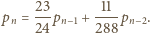
Wraz z wartościami początkowymi
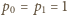 wyznacza
ona cały ciąg
wyznacza
ona cały ciąg
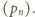 Numerycznie można się przekonać, że
Numerycznie można się przekonać, że
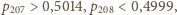 a zatem liczba, o którą pyta zadanie,
wynosi
a zatem liczba, o którą pyta zadanie,
wynosi
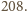 Oczywiście można też uzyskać zwykłą metodą
rozwiązanie tej ostatniej rekurencji w postaci
Oczywiście można też uzyskać zwykłą metodą
rozwiązanie tej ostatniej rekurencji w postaci
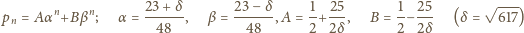
i zauważyć, że
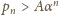 dla
dla
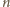 nieparzystych,
nieparzystych,
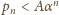 dla
dla
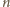 parzystych. Wystarczy więc sprawdzić, że
parzystych. Wystarczy więc sprawdzić, że
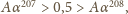 czyli że liczba
czyli że liczba
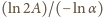 leży
pomiędzy
leży
pomiędzy
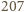 i
i
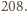 Tak w istocie jest; jej przybliżona wartość
wynosi
Tak w istocie jest; jej przybliżona wartość
wynosi
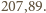
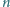 wybieramy losowo jedno. Wyznaczyć
najmniejszą liczbę naturalną
wybieramy losowo jedno. Wyznaczyć
najmniejszą liczbę naturalną
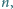 dla której bardziej prawdopodobne jest
wylosowanie słowa, w którym litery alfa i omega co najmniej raz sąsiadują,
niż słowa bez tej własności.
dla której bardziej prawdopodobne jest
wylosowanie słowa, w którym litery alfa i omega co najmniej raz sąsiadują,
niż słowa bez tej własności.

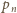 będzie prawdopodobieństwem wylosowania słowa dobrego,
tj. takiego, w którym dwie wyróżnione litery nie sąsiadują, zaś
będzie prawdopodobieństwem wylosowania słowa dobrego,
tj. takiego, w którym dwie wyróżnione litery nie sąsiadują, zaś
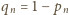 prawdopodobieństwem wylosowania słowa złego. Zapiszmy
te wartości jako sumy
prawdopodobieństwem wylosowania słowa złego. Zapiszmy
te wartości jako sumy
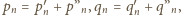 gdzie pojedynczy
prim odpowiada sytuacjom, gdy ostatnia litera słowa jest niewyróżniona,
a podwójny prim – sytuacjom, gdy ostatnia litera jest wyróżniona. Mamy
zależności rekurencyjne
gdzie pojedynczy
prim odpowiada sytuacjom, gdy ostatnia litera słowa jest niewyróżniona,
a podwójny prim – sytuacjom, gdy ostatnia litera jest wyróżniona. Mamy
zależności rekurencyjne
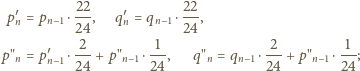
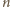 -słowo, zakończone jedną
z wyróżnionych liter, można uzyskać z dowolnego złego
-słowo, zakończone jedną
z wyróżnionych liter, można uzyskać z dowolnego złego
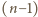 -słowa
(dopisując na końcu jedną z tych dwóch liter), bądź z dobrego
-słowa
(dopisując na końcu jedną z tych dwóch liter), bądź z dobrego
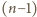 -słowa, zakończonego wyróżnioną literą (dopisując drugą
wyróżnioną literę); uzasadnienie pozostałych zależności jest podobne.
Odejmując dwie ostatnie równości otrzymujemy
-słowa, zakończonego wyróżnioną literą (dopisując drugą
wyróżnioną literę); uzasadnienie pozostałych zależności jest podobne.
Odejmując dwie ostatnie równości otrzymujemy
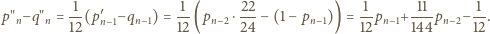
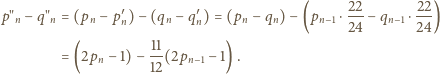
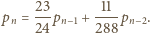
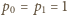 wyznacza
ona cały ciąg
wyznacza
ona cały ciąg
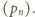 Numerycznie można się przekonać, że
Numerycznie można się przekonać, że
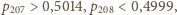 a zatem liczba, o którą pyta zadanie,
wynosi
a zatem liczba, o którą pyta zadanie,
wynosi
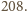 Oczywiście można też uzyskać zwykłą metodą
rozwiązanie tej ostatniej rekurencji w postaci
Oczywiście można też uzyskać zwykłą metodą
rozwiązanie tej ostatniej rekurencji w postaci
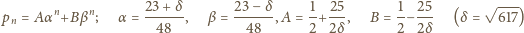
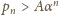 dla
dla
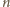 nieparzystych,
nieparzystych,
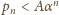 dla
dla
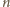 parzystych. Wystarczy więc sprawdzić, że
parzystych. Wystarczy więc sprawdzić, że
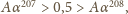 czyli że liczba
czyli że liczba
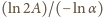 leży
pomiędzy
leży
pomiędzy
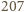 i
i
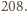 Tak w istocie jest; jej przybliżona wartość
wynosi
Tak w istocie jest; jej przybliżona wartość
wynosi