Z armaty do muchy»Zadanie 3
o zadaniu...
- Zadanie pochodzi z artykułu Z armaty do muchy
- Publikacja w Delcie: styczeń 2016
- Publikacja elektroniczna: 01-01-2016
- Artykuł źródłowy w wersji do druku [application/pdf]: (60 KB)
W dwóch urnach jest po 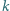 kul, każda z kul jest biała lub czarna. Z każdej z urn
kul, każda z kul jest biała lub czarna. Z każdej z urn  -krotnie losujemy kulę ze zwracaniem. Dla jakich wartości
-krotnie losujemy kulę ze zwracaniem. Dla jakich wartości 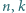 i dla jakiego układu kolorów kul prawdopodobieństwo wylosowania samych białych kul z pierwszej urny jest równe prawdopodobieństwu wylosowania z drugiej urny wszystkich kul jednego koloru?
i dla jakiego układu kolorów kul prawdopodobieństwo wylosowania samych białych kul z pierwszej urny jest równe prawdopodobieństwu wylosowania z drugiej urny wszystkich kul jednego koloru?

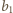 i
i 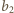 oznaczają liczby białych kul odpowiednio w pierwszej i drugiej urnie. Prawdopodobieństwo, że z pierwszej urny
oznaczają liczby białych kul odpowiednio w pierwszej i drugiej urnie. Prawdopodobieństwo, że z pierwszej urny  -krotnie wylosowano białą kulę równe jest
-krotnie wylosowano białą kulę równe jest 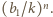 Podobnie wyznaczamy odpowiednie prawdopodobieństwa dla drugiej urny i równość z treści zadania przybiera postać
Podobnie wyznaczamy odpowiednie prawdopodobieństwa dla drugiej urny i równość z treści zadania przybiera postać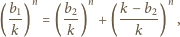
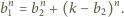
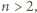 to z WTwF musi być
to z WTwF musi być 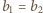 i
i 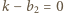 lub
lub 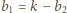 i
i 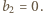 To prowadzi do rozwiązań
To prowadzi do rozwiązań 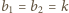 lub
lub  i
i 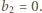
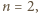 równanie spełniają wszystkie trójki pitagorejskie i dla każdej z nich są dwa rozwiązania.
równanie spełniają wszystkie trójki pitagorejskie i dla każdej z nich są dwa rozwiązania.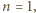 to prawdopodobieństwo, że wszystkie kule wylosowane z drugiej urny są jednego koloru jest równe 1, więc rozwiązaniem jest
to prawdopodobieństwo, że wszystkie kule wylosowane z drugiej urny są jednego koloru jest równe 1, więc rozwiązaniem jest