Google w łańcuchach
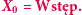 W roku 2009 słowem dziesięciolecia stowarzyszenie American Dialect Society ogłosiło czasownik to google, którego polski odpowiednik - guglować/guglać - omawiany jest już na stronach Słownika Języka Polskiego, PWN. Nic dziwnego, wszak korzystanie z wyszukiwarki Google stało się elementem codzienności większości z nas i nie mamy skrupułów przed zadawaniem jej pytań o najbłahsze sprawy. Idąc za myślą przewodnią tego numeru Delty, o nieoczekiwanych związkach teorii z rzeczywistością, pokażemy, co wspólnego ma wszędobylska wyszukiwarka z teorią łańcuchów Markowa, sformułowaną w początkach XX wieku.
W roku 2009 słowem dziesięciolecia stowarzyszenie American Dialect Society ogłosiło czasownik to google, którego polski odpowiednik - guglować/guglać - omawiany jest już na stronach Słownika Języka Polskiego, PWN. Nic dziwnego, wszak korzystanie z wyszukiwarki Google stało się elementem codzienności większości z nas i nie mamy skrupułów przed zadawaniem jej pytań o najbłahsze sprawy. Idąc za myślą przewodnią tego numeru Delty, o nieoczekiwanych związkach teorii z rzeczywistością, pokażemy, co wspólnego ma wszędobylska wyszukiwarka z teorią łańcuchów Markowa, sformułowaną w początkach XX wieku.
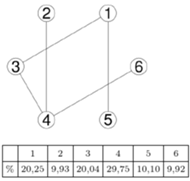
 Powiedzmy, że zwiedzamy graf spójny w taki sposób, że po znalezieniu się w danym wierzchołku, w kolejnym kroku odwiedzamy któregoś z jego sąsiadów, każdego z tym samym prawdopodobieństwem. Dla przykładu, kolejnymi odwiedzonymi wierzchołkami przy spacerowaniu po grafie na marginesie mogłyby być 1, 3, 4, 2, 4, 6,... Tabela przedstawia procentowy czas spędzony w poszczególnych wierzchołkach w pewnej symulacji 10 000 kroków zwiedzania tego grafu. Zauważmy, że przedstawione wartości wydają się mocno powiązane ze stopniami (czyli liczbami sąsiadów) poszczególnych wierzchołków. Oczywiście nie jest to wcale przypadek, co niebawem wyjaśnimy.
Powiedzmy, że zwiedzamy graf spójny w taki sposób, że po znalezieniu się w danym wierzchołku, w kolejnym kroku odwiedzamy któregoś z jego sąsiadów, każdego z tym samym prawdopodobieństwem. Dla przykładu, kolejnymi odwiedzonymi wierzchołkami przy spacerowaniu po grafie na marginesie mogłyby być 1, 3, 4, 2, 4, 6,... Tabela przedstawia procentowy czas spędzony w poszczególnych wierzchołkach w pewnej symulacji 10 000 kroków zwiedzania tego grafu. Zauważmy, że przedstawione wartości wydają się mocno powiązane ze stopniami (czyli liczbami sąsiadów) poszczególnych wierzchołków. Oczywiście nie jest to wcale przypadek, co niebawem wyjaśnimy.
 Załóżmy, że przeglądamy strony internetowe w bezmyślny sposób (nie róbcie tego w domu!), za każdym razem klikając w losowo wybrany odnośnik na stronie, na jakiej się znaleźliśmy. Gdyby procentowa liczba odwiedzin danej strony (na przykład deltami.edu.pl) stabilizowała się na pewnej granicznej wartości, to byłoby rozsądnie uznać tę wartość za miarę ważności tej strony - im jest większa ta wartość, tym częściej trafialibyśmy na daną stronę, "losowo" przeglądając Internet. Na pierwszy rzut oka nie wiadomo jednak, jak tę wartość obliczyć - pomogą nam w tym wspomniane we wstępie łańcuchy Markowa.
Załóżmy, że przeglądamy strony internetowe w bezmyślny sposób (nie róbcie tego w domu!), za każdym razem klikając w losowo wybrany odnośnik na stronie, na jakiej się znaleźliśmy. Gdyby procentowa liczba odwiedzin danej strony (na przykład deltami.edu.pl) stabilizowała się na pewnej granicznej wartości, to byłoby rozsądnie uznać tę wartość za miarę ważności tej strony - im jest większa ta wartość, tym częściej trafialibyśmy na daną stronę, "losowo" przeglądając Internet. Na pierwszy rzut oka nie wiadomo jednak, jak tę wartość obliczyć - pomogą nam w tym wspomniane we wstępie łańcuchy Markowa.
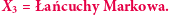 Łańcuchy Markowa stanowią matematyczny model dla następującej (mało rzeczywistej, ale mam nadzieję dość obrazowej) sytuacji: wyobraźmy sobie układ
Łańcuchy Markowa stanowią matematyczny model dla następującej (mało rzeczywistej, ale mam nadzieję dość obrazowej) sytuacji: wyobraźmy sobie układ 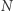 miast (ponumerowanych liczbami od 1 do
miast (ponumerowanych liczbami od 1 do 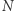 ). W każdym z nich znajduje się teleport, który w losowy sposób wybiera miasto, do którego przenosi użytkownika. Niech teleport w mieście
). W każdym z nich znajduje się teleport, który w losowy sposób wybiera miasto, do którego przenosi użytkownika. Niech teleport w mieście 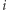 przenosi do miasta
przenosi do miasta 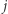 z prawdopodobieństwem
z prawdopodobieństwem 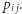 Załóżmy, że postanowiliśmy pozwiedzać miasta, codziennie korzystając (jednokrotnie) z zamieszczonych w nich teleportów.
Załóżmy, że postanowiliśmy pozwiedzać miasta, codziennie korzystając (jednokrotnie) z zamieszczonych w nich teleportów.
Przyjmijmy, że miejsce startu ( "dzień zero") jest losowe; z prawdopodobieństwem 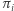 jest to miasto
jest to miasto 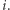 Z jakim prawdopodobieństwem pierwszego dnia znajdziemy się w mieście
Z jakim prawdopodobieństwem pierwszego dnia znajdziemy się w mieście 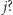 Szansa na rozpoczęcie z
Szansa na rozpoczęcie z 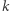 -tego miasta i przejście do
-tego miasta i przejście do 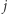 -tego wynosi
-tego wynosi 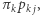 a zatem prawdopodobieństwo odwiedzenia
a zatem prawdopodobieństwo odwiedzenia 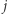 -tego miasta pierwszego dnia to
-tego miasta pierwszego dnia to 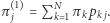 Z rozkładu w "dniu zero"
Z rozkładu w "dniu zero" 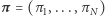 otrzymaliśmy rozkład w pierwszym dniu
otrzymaliśmy rozkład w pierwszym dniu 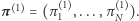 W tym sensie prawdopodobieństwa
W tym sensie prawdopodobieństwa 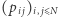 określają nam przekształcenie
określają nam przekształcenie 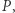 które z jednego rozkładu tworzy inny.
które z jednego rozkładu tworzy inny.
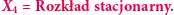 Przy założeniu (*), przedstawionym na marginesie,
Przy założeniu (*), przedstawionym na marginesie,  -ta iteracja przekształcenia
-ta iteracja przekształcenia 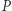 jest przekształceniem zwężającym, tzn. zmniejsza odległość między rozkładami o ustalony z góry czynnik. Aby to stwierdzenie miało sens, musimy doprecyzować odległość między rozkładami - u nas będzie to
jest przekształceniem zwężającym, tzn. zmniejsza odległość między rozkładami o ustalony z góry czynnik. Aby to stwierdzenie miało sens, musimy doprecyzować odległość między rozkładami - u nas będzie to 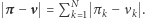 W tej sytuacji z twierdzenia Banacha o punkcie stałym wynika, że istnieje punkt stały przekształcenia
W tej sytuacji z twierdzenia Banacha o punkcie stałym wynika, że istnieje punkt stały przekształcenia 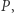 czyli taki rozkład
czyli taki rozkład 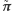 (nazywany stacjonarnym), że
(nazywany stacjonarnym), że 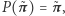 tzn. prawdopodobieństwo wystartowania z
tzn. prawdopodobieństwo wystartowania z 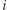 -tego miasta jest takie samo, jak prawdopodobieństwo znalezienia się w nim pierwszego (więc również drugiego, trzeciego, ...) dnia. Z twierdzenia Banacha wynika również, że rozkład
-tego miasta jest takie samo, jak prawdopodobieństwo znalezienia się w nim pierwszego (więc również drugiego, trzeciego, ...) dnia. Z twierdzenia Banacha wynika również, że rozkład 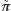 może zostać uzyskany z dowolnego rozkładu
może zostać uzyskany z dowolnego rozkładu 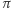 poprzez iterację
poprzez iterację 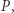 tzn. ciąg
tzn. ciąg 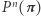 (gdzie
(gdzie 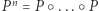 ) jest coraz lepszym przybliżeniem
) jest coraz lepszym przybliżeniem 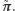
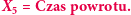 Kiedy rozkład
Kiedy rozkład 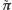 istnieje, to (zakładając
istnieje, to (zakładając 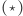 ) ma pewną ciekawą własność -
) ma pewną ciekawą własność - 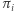 jest równy odwrotności średniego czasu oczekiwania na powrót do
jest równy odwrotności średniego czasu oczekiwania na powrót do 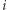 -tego wierzchołka, co teraz uzasadnimy. Załóżmy, że rozpoczęliśmy naszą wędrówkę, losując startowe miasto z rozkładu stacjonarnego. Pewnego dnia znaleźliśmy się w
-tego wierzchołka, co teraz uzasadnimy. Załóżmy, że rozpoczęliśmy naszą wędrówkę, losując startowe miasto z rozkładu stacjonarnego. Pewnego dnia znaleźliśmy się w 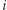 -tym mieście i zastanawiamy się, kiedy doń wrócimy. Liczbę dni, jakie upłyną do pierwszego powrotu, oznaczmy jako
-tym mieście i zastanawiamy się, kiedy doń wrócimy. Liczbę dni, jakie upłyną do pierwszego powrotu, oznaczmy jako 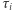 - jest to pewna losowa wielkość. Niech
- jest to pewna losowa wielkość. Niech 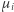 będzie wartością oczekiwaną
będzie wartością oczekiwaną 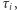 tzn.
tzn.
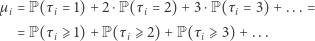 |
(1) |
Niech 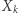 będzie numerem miasta odwiedzonego
będzie numerem miasta odwiedzonego 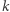 -tego dnia i niech
-tego dnia i niech 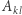 oznacza zdarzenie, że
oznacza zdarzenie, że 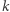 -tego dnia byliśmy w mieście
-tego dnia byliśmy w mieście 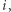 do którego nie wróciliśmy przez kolejnych
do którego nie wróciliśmy przez kolejnych 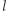 dni. Zauważmy, że
dni. Zauważmy, że 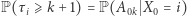 oraz
oraz 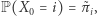 gdzie Przez
gdzie Przez 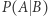 oznaczamy prawdopodobieństwo zajścia zdarzenia
oznaczamy prawdopodobieństwo zajścia zdarzenia 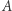 pod warunkiem zajścia zdarzenia
pod warunkiem zajścia zdarzenia 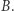 Korzystając z (1), dostajemy
Korzystając z (1), dostajemy
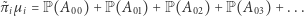 |
(2) |
Ponieważ wyszliśmy od rozkładu stacjonarnego, więc 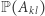 zależy tylko od
zależy tylko od 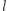 (co może wymagać chwili zastanowienia), zatem suma pierwszych
(co może wymagać chwili zastanowienia), zatem suma pierwszych 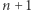 składników w (2) to
składników w (2) to
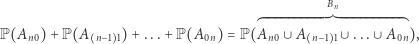 |
(3) |
gdyż zdarzenia 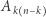 są rozłączne, ponadto ich suma
są rozłączne, ponadto ich suma 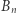 to zdarzenie, że w pierwszych
to zdarzenie, że w pierwszych  dniach odwiedziliśmy co najmniej raz
dniach odwiedziliśmy co najmniej raz 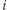 -te miasto. Z założenia
-te miasto. Z założenia 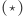 można wywnioskować, że
można wywnioskować, że 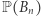 jest zbieżne do 1, a zatem z (2) i (3) wynika
jest zbieżne do 1, a zatem z (2) i (3) wynika 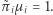
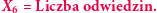 Na zakończenie teoretycznych rozważań zauważmy, że skoro wartość oczekiwana liczby dni potrzebnych na powrót do
Na zakończenie teoretycznych rozważań zauważmy, że skoro wartość oczekiwana liczby dni potrzebnych na powrót do 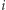 -tego miasta wynosi
-tego miasta wynosi 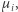 to średnio "raz na
to średnio "raz na 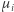 " kroków wracamy do
" kroków wracamy do 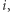 zatem jeśli
zatem jeśli 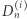 jest liczbą dni spędzonych w
jest liczbą dni spędzonych w 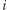 -tym mieście podczas pierwszych
-tym mieście podczas pierwszych 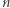 dni, to
dni, to 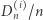 staje się coraz bliższe
staje się coraz bliższe 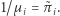 Rozumowanie to można nietrudno uściślić przy użyciu Mocnego Prawa Wielkich Liczb.
Rozumowanie to można nietrudno uściślić przy użyciu Mocnego Prawa Wielkich Liczb.
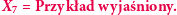 Zauważmy, że nasz spacer po grafie spójnym odpowiada łańcuchowi Markowa o prawdopodobieństwie przejścia
Zauważmy, że nasz spacer po grafie spójnym odpowiada łańcuchowi Markowa o prawdopodobieństwie przejścia 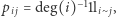 gdzie
gdzie 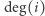 to stopień wierzchołka
to stopień wierzchołka 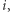 a
a 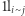 przyjmuje wartość 1, jeśli
przyjmuje wartość 1, jeśli 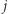 jest sąsiadem
jest sąsiadem 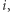 oraz 0 w przeciwnym przypadku. Niech
oraz 0 w przeciwnym przypadku. Niech  będzie liczbą krawędzi. Łatwo uzasadnić, że suma stopni wierzchołków w grafie wynosi
będzie liczbą krawędzi. Łatwo uzasadnić, że suma stopni wierzchołków w grafie wynosi 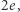 a zatem wagi
a zatem wagi 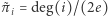 stanowią rozkład. Zwróćmy uwagę, że
stanowią rozkład. Zwróćmy uwagę, że

zatem 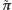 jest rozkładem stacjonarnym - uzasadnia to zaobserwowany wcześniej fenomen dotyczący średniego czasu przebywania w danym wierzchołku. Dość nieoczekiwanym stąd wnioskiem jest to, że średnia liczba odwiedzin jest w tym przypadku własnością lokalną i zależy tylko od stopnia wierzchołka i liczby krawędzi; bez znaczenia jest struktura pozostałej części grafu (jak również liczba wierzchołków).
jest rozkładem stacjonarnym - uzasadnia to zaobserwowany wcześniej fenomen dotyczący średniego czasu przebywania w danym wierzchołku. Dość nieoczekiwanym stąd wnioskiem jest to, że średnia liczba odwiedzin jest w tym przypadku własnością lokalną i zależy tylko od stopnia wierzchołka i liczby krawędzi; bez znaczenia jest struktura pozostałej części grafu (jak również liczba wierzchołków).
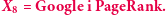 Wróćmy do losowego przeglądania stron. Oczywiście, ono również określa nam pewien łańcuch Markowa. Gdyby spełnione było założenie
Wróćmy do losowego przeglądania stron. Oczywiście, ono również określa nam pewien łańcuch Markowa. Gdyby spełnione było założenie 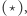 to średnia liczba odwiedzin danej strony (czyli szukana wartość strony) zbiegałaby do wartości rozkładu stacjonarnego dla tej strony. Niestety podczas opisanego spacerowania po stronach internetowych moglibyśmy wpaść w pewne pułapki; możemy na przykład trafić na stronę bez żadnego odnośnika lub w inny sposób naruszyć
to średnia liczba odwiedzin danej strony (czyli szukana wartość strony) zbiegałaby do wartości rozkładu stacjonarnego dla tej strony. Niestety podczas opisanego spacerowania po stronach internetowych moglibyśmy wpaść w pewne pułapki; możemy na przykład trafić na stronę bez żadnego odnośnika lub w inny sposób naruszyć 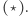 Celem rozwiązania tego problemu wprowadza się niezerowe prawdopodobieństwo "teleportacji" - przed kliknięciem w dowolny odnośnik mamy szansę
Celem rozwiązania tego problemu wprowadza się niezerowe prawdopodobieństwo "teleportacji" - przed kliknięciem w dowolny odnośnik mamy szansę 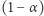 (lub 1, jeśli na danej stronie nie ma odnośników) na przeskoczenie do losowo wybranej strony, każdej z jednakowym prawdopodobieństwem. W odróżnieniu od wcześniejszego przykładu, nie możemy jednak w prosty sposób wskazać rozkładu stacjonarnego, a dokładne rozwiązanie odpowiedniego układu równań nie wchodzi w grę ze względu na ogromną liczbę stron internetowych. Wiemy jednak, że zgodnie z twierdzeniem Banacha o punkcie stałym możemy przybliżyć rozkład stacjonarny poprzez rozpoczęcie od dowolnego rozkładu (np.
(lub 1, jeśli na danej stronie nie ma odnośników) na przeskoczenie do losowo wybranej strony, każdej z jednakowym prawdopodobieństwem. W odróżnieniu od wcześniejszego przykładu, nie możemy jednak w prosty sposób wskazać rozkładu stacjonarnego, a dokładne rozwiązanie odpowiedniego układu równań nie wchodzi w grę ze względu na ogromną liczbę stron internetowych. Wiemy jednak, że zgodnie z twierdzeniem Banacha o punkcie stałym możemy przybliżyć rozkład stacjonarny poprzez rozpoczęcie od dowolnego rozkładu (np. 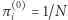 ) i powtarzanie
) i powtarzanie
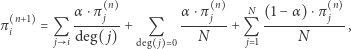 |
(4) |
gdzie pierwsza suma obejmuje wszystkie strony wskazujące na 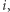 a druga wszystkie "strony puste". Ten sposób mierzenia i obliczania ważności strony został zaproponowany przez Larry'ego Page'a i Sergeya Brina w 1997 roku, ochrzczony PageRank i wykorzystany w stworzonej przez nich wyszukiwarce Google jako istotny czynnik przy decydowaniu o kolejności wyświetlanych stron internetowych. I chociaż informacja o wartościach PageRanku nie jest już dostępna publicznie, wiele wskazuje na to, że ciągle odgrywa on niemałą rolę w sposobie, w jaki Google sortuje wyniki. Czytelnikom Zainteresowanym polecam samodzielne wyguglanie szczegółów.
a druga wszystkie "strony puste". Ten sposób mierzenia i obliczania ważności strony został zaproponowany przez Larry'ego Page'a i Sergeya Brina w 1997 roku, ochrzczony PageRank i wykorzystany w stworzonej przez nich wyszukiwarce Google jako istotny czynnik przy decydowaniu o kolejności wyświetlanych stron internetowych. I chociaż informacja o wartościach PageRanku nie jest już dostępna publicznie, wiele wskazuje na to, że ciągle odgrywa on niemałą rolę w sposobie, w jaki Google sortuje wyniki. Czytelnikom Zainteresowanym polecam samodzielne wyguglanie szczegółów.
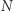 liczb nieujemnych, sumujących się do 1.
liczb nieujemnych, sumujących się do 1.