Kto ma rację?
Skończył się mecz - najważniejsze wydarzenie tygodnia. Po burzliwej wymianie zdań na jego temat trzej przyjaciele: Długi, Gruby i Ludek wracali do domu. Nagle Ludek zapytał o zadanie z matematyki, które było na jutro. Długi i Gruby stanęli jak zaczarowani. Zapomnieli o zadaniu. W necie na chwilę się zagotowało! Nastała cisza przerywana wiadomościami przychodzącymi na komórki. Nikt z klasy jeszcze zadania nie zrobił. Zadanie było krótkie: Jak gruba powinna być moneta, aby szansa, że wyląduje ona na krawędzi, wynosiła 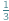 ?
?
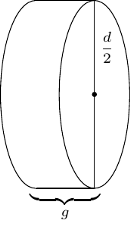
Rys. 1
Wszyscy zgodzili się przyjąć uproszczenie, że moneta jest jednorodnym, symetrycznym walcem. Gruby, który początkowo zbladł i spocił się, nieśmiało zgłosił pomysł. Posmarujemy deskę miodem (by rzucana moneta nie odbijała się i nie toczyła), sklejając pięciogroszówki stworzymy kilka wariantów "grubych" monet i na podstawie eksperymentu wybierzemy odpowiedź.
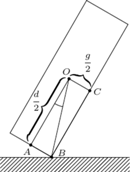
Rys. 2
Długi uznał, że zadanie jest łatwe i szkoda miodu. To, na której "stronie" wyląduje moneta, jest proporcjonalne do pola powierzchni poszczególnych "stron". Zatem warunki zadania będą spełnione, gdy pole powierzchni bocznej walca będzie równe polu podstawy. Obliczył (Rys. 1):

I triumfalnie oznajmił: grubość monety powinna stanowić 25% długości jej średnicy. Życie jest piękne, a my jesteśmy genialni! Jednak Ludek, który lubił fizykę, nad czymś rozmyślał. Po chwili powiedział, że widzi inne rozwiązanie. Poza przypadkiem, gdy moneta wylądowała od razu na swojej podstawie lub na krawędzi, musiała wylądować koślawie. Miodek chwyta koślawie padającą monetę, która pod wpływem siły ciężkości ostatecznie wyląduje na tej stronie, na której rzut jej środka ciężkości znajdzie się we wnętrzu powłoki wypukłej rzutu tej strony. To zaś zależy od kąta 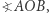 i tu zrobił rysunek (Rys. 2). Warunki zadania będą spełnione, gdy kąt
i tu zrobił rysunek (Rys. 2). Warunki zadania będą spełnione, gdy kąt 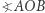 będzie równy
będzie równy 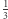 kąta prostego
kąta prostego 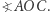 Przy oznaczeniach z rysunku
Przy oznaczeniach z rysunku

Oznacza to, że grubość monety spełniającej warunki zadania powinna wynosić 57,7% długości jej średnicy. No to mamy problem, przyznali chłopcy, ale najważniejsze było dla nich, że na lekcję nie pójdą z niczym.
Gruby po powrocie do domu zaczął szukać czegoś na temat zadania w necie. Znalazł fascynującą historię. Pewnego razu, gdy John von Neumann wraz z uczonymi kolegami wysiadał z taksówki, taksówkarz zadał mu pytanie, które jest treścią naszego zadania. Ku niemałemu zdziwieniu kolegów, po jakichś 15-20 sekundach von Neumann ocenił, że grubość takiej monety powinna stanowić około 35% długości jej średnicy. Jak rozumował von Neumann, możemy się tylko domyślać.
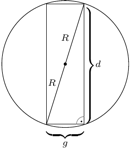
Rys. 3
Federick Mosteller widział to tak (Fifty challenging problems in probability with solutions, Dover Publ., N. York, 1965, Problem 38). Na monecie (= walcu) opisana jest sfera o promieniu 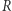 (Rys. 3). Tę sferę tworzą wszystkie możliwe wektory momentu siły znormalizowane do długości
(Rys. 3). Tę sferę tworzą wszystkie możliwe wektory momentu siły znormalizowane do długości 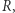 zaczepione w środku ciężkości walca. Są to też wszystkie możliwe kierunki rzutu środka ciężkości walca. Aby spełnić warunki zadania, trzecia część powierzchni kuli powinna przypadać na sytuację, gdy rzut środka ciężkości pozwala na lądowanie monety na krawędzi. Ponieważ pole warstwy kulistej jest proporcjonalne do jej grubości
zaczepione w środku ciężkości walca. Są to też wszystkie możliwe kierunki rzutu środka ciężkości walca. Aby spełnić warunki zadania, trzecia część powierzchni kuli powinna przypadać na sytuację, gdy rzut środka ciężkości pozwala na lądowanie monety na krawędzi. Ponieważ pole warstwy kulistej jest proporcjonalne do jej grubości 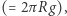 więc nasza moneta powinna mieć grubość równą
więc nasza moneta powinna mieć grubość równą 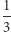 średnicy sfery opisanej na monecie. Zatem
średnicy sfery opisanej na monecie. Zatem

Pozostaje obliczyć grubość takiej monety w stosunku do jej średnicy. Tu wystarczy Pitagoras:

Kto ma rację?