Ostatni Mohikanin
Zacznijmy od następującego zadania: dwunastu Indian (dla ustalenia uwagi i zgrabności tytułu przyjmijmy, że pochodzą oni z plemienia Mohikanów) siedzi dookoła ogniska i pali fajkę pokoju. Procedura rozpoczyna się rzecz jasna od Wodza, który po zapaleniu rzuca zdobytą od bladych twarzy symetryczną monetą i w zależności od wyniku podaje fajkę na lewo albo na prawo. Kolejny Indianin robi to samo - pali faję, rzuca monetą i podaje dalej (fajkę, nie monetę). Nietrudno uwierzyć, że prędzej czy później fajka wpadnie w ręce ostatniego Indianina, który jej wcześniej nie palił (będzie to tytułowy ostatni Mohikanin)...
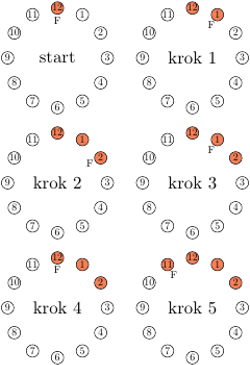
Początek przykładowej trajektorii fajki (F). Kolorem oznaczeni są Indianie, którzy zdążyli zapalić.
Oczywiście, na samym początku nie jesteśmy w stanie stwierdzić, kto nim będzie, gdyż przedstawiona procedura jest losowa. Zapewne jednak niektórzy z Mohikanów mają większą szansę na bycie ostatnim Mohikaninem niż inni. Naturalne jest w tej sytuacji pytanie: który z nich ma na to szansę największą?
Wydaje się, że Indianie o numerach 1 i 11 nie są dobrymi kandydatami - każdy z nich ma prawdopodobieństwo 50% otrzymania fajki już w pierwszym ruchu. Analiza sytuacji Indian o numerach 2 i 10 zdaje się bardziej skomplikowana, intuicja podpowiada jednak, że ich szansa na bycie ostatnimi jest większa niż sąsiadów Wodza. Idąc tym tropem, największą szansę na bycie ostatnim powinien mieć Indianin siedzący najdalej od Wodza, czyli ten o numerze 6. Przedstawionym domysłom daleko jednak do matematycznej ścisłości i nic dziwnego - prowadzą bowiem do błędnych wniosków. Tak naprawdę każdy Indianin (poza Wodzem) ma to samo prawdopodobieństwo zapalenia fajki jako ostatni! Jak to możliwe?
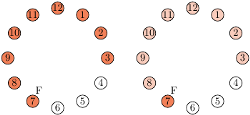
Moment pierwszego dojścia do bezpośredniego sąsiedztwa "szóstki" oraz to, jak wygląda ta sytuacja z punktu widzenia jego potencjalnej "ostatniości".
Z punktu widzenia Mohikanina numer 1 sytuacja wygląda następująco: fajka znajduje się u jego sąsiada (Wodza) i pytamy o prawdopodobieństwo tego, że fajka zdąży odwiedzić pozostałych Indian, zanim trafi do "jedynki". Rozważmy teraz Indianina o numerze 6. Zauważmy, że niezależnie od trajektorii fajki przyjdzie taki moment, że fajka po raz pierwszy wyląduje w bezpośrednim sąsiedztwie "szóstki". Jeśli ma on palić jako ostatni, to tak czy inaczej począwszy od tego momentu fajka musi odwiedzić wszystkie wierzchołki poza "szóstką", zanim do niego trafi (ze sposobu przekazywania fajki wynika, iż dotychczas odwiedzone wierzchołki nie mają znaczenia, gdyż i tak będą musiały zostać odwiedzone jeszcze raz). Jest to dokładnie ta sama sytuacja, jaka na początku była widziana oczami Indianina numer 1. Pokazaliśmy zatem, że
na pewno dojdzie do zdarzenia, pod warunkiem którego szansa "szóstki" na bycie ostatnim jest taka, jak szansa (bezwarunkowa) "jedynki" na bycie ostatnim.
Oznacza to, że (bezwarunkowa) szansa "szóstki" na bycie ostatnim jest taka sama, jak szansa jedynki - oczywiście w ten sam sposób możemy pokazać, że szansa dowolnego Indianina (poza Wodzem) na bycie ostatnim Mohikaninem jest taka sama, wynosi zatem 1/11.
Wyobraźmy sobie teraz, że mamy do czynienia z rzutkimi Indianami, którzy nie mają nic przeciwko rzucaniu fajką pokoju i czynią to bardzo celnie. Reguły gry są podobne - po wypaleniu fajki każdy z Indian z równym prawdopodobieństwem wybiera któregoś z pozostałych, aby przekazać mu fajkę. Oczywiście, ze względu na symetrię sytuacji, wciąż jest prawdą to, że każdy z Indian ma to samo prawdopodobieństwo zostania ostatnim Mohikaninem, niezależnie od początkowego położenia fajki. A co by było, gdyby między nimi występowały jakieś animozje, tzn. nie każda para Indian byłaby skłonna przekazać między sobą fajkę? Czy istnieje inna struktura sympatii i antypatii poza cyklem (każdy z Indian lubi wyłącznie swoich sąsiadów; rozważyliśmy ten przypadek w pierwszej części artykułu) i kliką (każdych dwóch Indian darzy się sympatią), w której zachodzi przedstawiona wcześniej własność? Okazuje się, że nie, co uzasadniamy dalej.
Rozpoczniemy od przedstawienia naszego problemu w języku teorii grafów. Mamy do czynienia z grafem 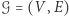 o
o 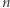 wierzchołkach, po którym w losowy sposób spacerujemy - stojąc w dowolnym wierzchołku, z jednakowym prawdopodobieństwem wybieramy dowolnego jego sąsiada, aby przejść do niego w następnym kroku. Niech
wierzchołkach, po którym w losowy sposób spacerujemy - stojąc w dowolnym wierzchołku, z jednakowym prawdopodobieństwem wybieramy dowolnego jego sąsiada, aby przejść do niego w następnym kroku. Niech 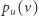 będzie prawdopodobieństwem zdarzenia, że wierzchołek
będzie prawdopodobieństwem zdarzenia, że wierzchołek  został odwiedzony jako ostatni, jeśli startowaliśmy z
został odwiedzony jako ostatni, jeśli startowaliśmy z 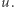 Interesujący nas warunek możemy teraz zapisać jako
Interesujący nas warunek możemy teraz zapisać jako
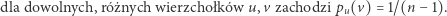 |
(  ) ) |
Załóżmy, że spełniony jest powyższy warunek i wybierzmy dowolne dwa niepołączone wierzchołki 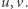 Niech
Niech 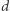 będzie stopniem
będzie stopniem 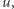 a
a 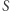 zbiorem jego sąsiadów. Korzystając ze wzoru na prawdopodobieństwo całkowite, dostajemy
zbiorem jego sąsiadów. Korzystając ze wzoru na prawdopodobieństwo całkowite, dostajemy 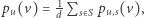 gdzie
gdzie 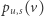 jest prawdopodobieństwem zakończenia na
jest prawdopodobieństwem zakończenia na  jeśli startowaliśmy od
jeśli startowaliśmy od  pod warunkiem zdarzenia, że pierwszym odwiedzonym wierzchołkiem był
pod warunkiem zdarzenia, że pierwszym odwiedzonym wierzchołkiem był  Zauważmy ponadto, że
Zauważmy ponadto, że

gdyż 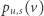 "obejmuje" wszystkie te spacery (liczone od
"obejmuje" wszystkie te spacery (liczone od  ), co
), co 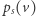 oraz te, które nie odwiedzały
oraz te, które nie odwiedzały 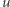 przed dotarciem do
przed dotarciem do 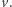 Gdyby istniał choć jeden taki spacer, mielibyśmy
Gdyby istniał choć jeden taki spacer, mielibyśmy 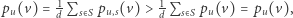 zatem sprzeczność. Nie istnieje więc spacer, który startuje z sąsiada
zatem sprzeczność. Nie istnieje więc spacer, który startuje z sąsiada 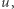 przechodzi (niekoniecznie jednokrotnie) przez wszystkie wierzchołki poza
przechodzi (niekoniecznie jednokrotnie) przez wszystkie wierzchołki poza 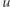 i
i 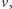 a na końcu odwiedza
a na końcu odwiedza  Wnioskujemy stąd, że
Wnioskujemy stąd, że
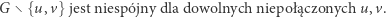 |
( 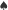 ) ) |
Okazuje się, że graf, który spełnia (  ) i (
) i ( 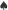 ), musi być łańcuchem albo kliką. Jest to ciekawe i przystępne zadanie z matematyki dyskretnej, które polecamy wykonać Czytelnikom Ambitnym. Czytelnikom Niecierpliwym polecamy zaś kliknięcie w coś, co znajduje się niedaleko i nadaje się do klikania. Howgh!
), musi być łańcuchem albo kliką. Jest to ciekawe i przystępne zadanie z matematyki dyskretnej, które polecamy wykonać Czytelnikom Ambitnym. Czytelnikom Niecierpliwym polecamy zaś kliknięcie w coś, co znajduje się niedaleko i nadaje się do klikania. Howgh!
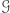 spełnia
spełnia 
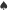
![[A]](/math/temat/matematyka/rachunek_prawdopodobienstwa/2018/06/26/Ostatni_Mohikanin/4x-4876f5d383153f8c66c92618c582b821de355692-im-33,33,33-FF,FF,FF.gif) istnieją dwa niepołączone wierzchołki;
istnieją dwa niepołączone wierzchołki;![[♠ + 1]](/math/temat/matematyka/rachunek_prawdopodobienstwa/2018/06/26/Ostatni_Mohikanin/5x-4876f5d383153f8c66c92618c582b821de355692-im-33,33,33-FF,FF,FF.gif) żaden wierzchołek nie ma stopnia
żaden wierzchołek nie ma stopnia 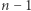 ;
;![[♣]](/math/temat/matematyka/rachunek_prawdopodobienstwa/2018/06/26/Ostatni_Mohikanin/7x-4876f5d383153f8c66c92618c582b821de355692-im-33,33,33-FF,FF,FF.gif)
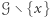 jest spójny dla dowolnego
jest spójny dla dowolnego  (inaczej
(inaczej 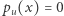 );
);![[3]](/math/temat/matematyka/rachunek_prawdopodobienstwa/2018/06/26/Ostatni_Mohikanin/11x-4876f5d383153f8c66c92618c582b821de355692-im-33,33,33-FF,FF,FF.gif) wszystkie wierzchołki mają stopień
wszystkie wierzchołki mają stopień 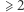 ;
;![[B + 4]](/math/temat/matematyka/rachunek_prawdopodobienstwa/2018/06/26/Ostatni_Mohikanin/13x-4876f5d383153f8c66c92618c582b821de355692-im-33,33,33-FF,FF,FF.gif) istnieje wierzchołek stopnia
istnieje wierzchołek stopnia 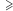 3 (oznaczmy go
3 (oznaczmy go  );
);![[2]](/math/temat/matematyka/rachunek_prawdopodobienstwa/2018/06/26/Ostatni_Mohikanin/16x-4876f5d383153f8c66c92618c582b821de355692-im-33,33,33-FF,FF,FF.gif) istnieje
istnieje  niepołączone z
niepołączone z  ;
;![[ 6 + ♠]](/math/temat/matematyka/rachunek_prawdopodobienstwa/2018/06/26/Ostatni_Mohikanin/19x-4876f5d383153f8c66c92618c582b821de355692-im-33,33,33-FF,FF,FF.gif)
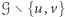 ma co najmniej dwie spójne składowe
ma co najmniej dwie spójne składowe 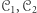 ;
;![[3]](/math/temat/matematyka/rachunek_prawdopodobienstwa/2018/06/26/Ostatni_Mohikanin/22x-4876f5d383153f8c66c92618c582b821de355692-im-33,33,33-FF,FF,FF.gif) istnieją takie
istnieją takie 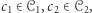 że
że 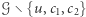 jest spójny;
jest spójny;![[ 8 + 5]](/math/temat/matematyka/rachunek_prawdopodobienstwa/2018/06/26/Ostatni_Mohikanin/25x-4876f5d383153f8c66c92618c582b821de355692-im-33,33,33-FF,FF,FF.gif)
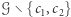 jest spójny;
jest spójny;![[7 + 8]](/math/temat/matematyka/rachunek_prawdopodobienstwa/2018/06/26/Ostatni_Mohikanin/27x-4876f5d383153f8c66c92618c582b821de355692-im-33,33,33-FF,FF,FF.gif)
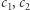 nie są połączone;
nie są połączone;![[♠ + 9 + 10]](/math/temat/matematyka/rachunek_prawdopodobienstwa/2018/06/26/Ostatni_Mohikanin/29x-4876f5d383153f8c66c92618c582b821de355692-im-33,33,33-FF,FF,FF.gif) sprzeczność!
sprzeczność!