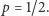Prawdopodobieństwo a informacja
Filozof może się zadowolić tym, że "wie, że nic nie wie". Fizyk zaś potrzebuje wiedzieć, ile nie wie...
Pojęcie entropii ma swoje źródło w termodynamice i jest związane z tym, jak bardzo nie znamy dokładnego mikrostanu układu. Tylko gdy wiemy o nim wszystko, możemy w pełni wykorzystać jego energię, przekształcając ją na inne formy. Gdy nie - część energii pozostaje niejako uwięziona.
Entropia jest równie cenna w teorii informacji - pozwala ściśle zmierzyć, jak dobrze możemy skompresować daną wiadomość oraz jak bardzo możemy niwelować szum przy jej przesyłaniu. Przydaje się ona również jako miara losowości i korelacji w różnych narzędziach statystycznych.
O ile entropia jest używana w języku potocznym jako chaos i nieuporządkowanie, to sama wielkość (a konkretniej, entropia Shannona) jest ściśle określona następującym wzorem:
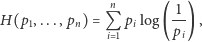 |
(*) |
gdzie 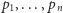 są prawdopodobieństwami możliwych wyników przeprowadzanego eksperymentu. Będziemy używać logarytmu o podstawie 2, co odpowiada mierzeniu entropii w bitach. Powyższy wzór ma wiele zastosowań i interpretacji.
są prawdopodobieństwami możliwych wyników przeprowadzanego eksperymentu. Będziemy używać logarytmu o podstawie 2, co odpowiada mierzeniu entropii w bitach. Powyższy wzór ma wiele zastosowań i interpretacji.
Ale zanim do nich przejdziemy, spójrzmy na kilka prostych przykładów. Gdy mamy jedną możliwość, entropia wynosi 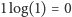 - wszak nie ma tu miejsca na losowość. Gdy rzucamy uczciwą monetą, entropia to
- wszak nie ma tu miejsca na losowość. Gdy rzucamy uczciwą monetą, entropia to 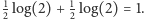 Entropia jest największa, gdy dla ustalonej liczby zdarzeń wszystkie są równoprawdopodobne - wtedy wynosi ona
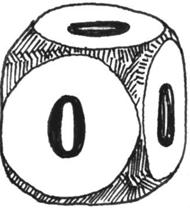
Entropia jest największa, gdy dla ustalonej liczby zdarzeń wszystkie są równoprawdopodobne - wtedy wynosi ona 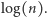 Dla kostki do gry z
Dla kostki do gry z 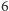 ścianami to
ścianami to 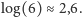
Warto pamiętać, że entropia jest zawsze miarą niewiedzy. Stąd np. kostka, na której widzimy wyrzucone dwa oczka, ma entropię zero. Dowiadujemy się dokładnie tyle, o ile entropia zmalała, tu:

Gdyby ktoś nam powiedział "wypadło jedno, dwa lub trzy oczka", nasza wiedza końcowa byłaby niepełna i dowiedzielibyśmy się 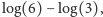 czyli 1 bit informacji.
czyli 1 bit informacji.
Dlaczego potrzebujemy w tym wzorze logarytmu? Gdy mamy dwa niezależne zdarzenia, chcemy, by ich entropia była sumą entropii składników. Powiedzmy, że chcemy dowiedzieć się, jaki jest znak zodiaku naszego obiektu westchnień oraz czy nas kocha. Nie powinno grać roli, czy dowiemy się jednej informacji naraz czy po kawałku. Oznaczymy prawdopodobieństwa znaków zodiaku jako 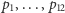 oraz uczucie do nas jako
oraz uczucie do nas jako 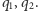 Tym samym prawdopodobieństwa poszczególnych, niezależnych zdarzeń to iloczyny
Tym samym prawdopodobieństwa poszczególnych, niezależnych zdarzeń to iloczyny  Zatem jak jest z entropią?
Zatem jak jest z entropią?

zatem entropia niezależnych zdarzeń dodaje się. W szczególności: 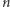 rzutów uczciwą monetą to
rzutów uczciwą monetą to 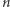 bitów entropii.
bitów entropii.
Na wzór na entropię Shannona można patrzeć również jak na średnią uzyskaną informację. Zobaczmy to na przykładzie gry w dwadzieścia pytań, w której jedna osoba wymyśla jakąś rzecz, a druga ma za zadanie zgadnąć, o co chodzi, zadając po kolei pytania na "tak" lub "nie". Można się zastanowić, czy warto zadawać pytania, które są z grubsza pół na pół (np. "Czy to jest żywe?"), czy też takie, w których jest niewielka szansa, że dużo się rozjaśni (np. "Czy to element biżuterii?").
Powiedzmy, że na starcie jest 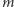 możliwych obiektów i każdy z nich jest równoprawdopodobny. Jeśli zadamy pytanie, dla
możliwych obiektów i każdy z nich jest równoprawdopodobny. Jeśli zadamy pytanie, dla 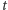 obiektów odpowiedzią jest "tak", dla
obiektów odpowiedzią jest "tak", dla 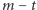 pozostałych - "nie". Wiąże się to bezpośrednio z prawdopodobieństwami odpowiedzi:
pozostałych - "nie". Wiąże się to bezpośrednio z prawdopodobieństwami odpowiedzi:

Zatem po uzyskaniu odpowiedzi zbiór możliwych obiektów zmniejsza się do 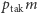 albo
albo 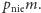 Po zadaniu dwóch pytań (dla uproszczenia przyjmując, że po zadaniu pierwszego drugie ma to samo prawdopodobieństwo udzielenia twierdzącej odpowiedzi) dostajemy
Po zadaniu dwóch pytań (dla uproszczenia przyjmując, że po zadaniu pierwszego drugie ma to samo prawdopodobieństwo udzielenia twierdzącej odpowiedzi) dostajemy 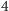 możliwości:
możliwości: 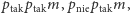
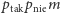 albo
albo 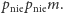 Wygramy w sytuacji, gdy po iluś pytaniach zredukujemy liczbę możliwości do tylko jednej. O ile może być w tym trochę szczęścia, to przy większej liczbie pytań (a mamy do dyspozycji ich aż
Wygramy w sytuacji, gdy po iluś pytaniach zredukujemy liczbę możliwości do tylko jednej. O ile może być w tym trochę szczęścia, to przy większej liczbie pytań (a mamy do dyspozycji ich aż 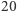 ), możemy śledzić, co się średnio stanie. Skoro przy dodawaniu kolejnych pytań prawdopodobieństwa się mnożą, to wielkością, którą chcemy uśredniać, jest wspomniany logarytm prawdopodobieństwa. Po jednym pytaniu dostajemy
), możemy śledzić, co się średnio stanie. Skoro przy dodawaniu kolejnych pytań prawdopodobieństwa się mnożą, to wielkością, którą chcemy uśredniać, jest wspomniany logarytm prawdopodobieństwa. Po jednym pytaniu dostajemy

- to samo co (*). Po zadaniu 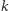 pytań dowiadujemy się średnio
pytań dowiadujemy się średnio 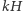 bitów informacji. Wielkość ta to
bitów informacji. Wielkość ta to 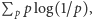 gdzie
gdzie 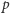 jest prawdopodobieństwem uzyskania poszczególnego ciągu odpowiedzi. Jeśli jej wartość dojdzie do
jest prawdopodobieństwem uzyskania poszczególnego ciągu odpowiedzi. Jeśli jej wartość dojdzie do  to średnio
to średnio  a zatem liczba możliwych obiektów zostanie zredukowana do jednej, czyli: zgadliśmy!
a zatem liczba możliwych obiektów zostanie zredukowana do jednej, czyli: zgadliśmy!
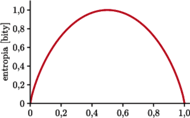
Entropia przy dwóch możliwościach, 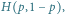 np. rzutu nieuczciwą monetą (
np. rzutu nieuczciwą monetą ( 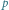 to prawdopodobieństwo orła) lub odpowiedzi na pytanie (
to prawdopodobieństwo orła) lub odpowiedzi na pytanie ( 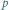 to prawdopodobieństwo "tak"). Maksimum, równe 1 bitowi, osiąga dla
to prawdopodobieństwo "tak"). Maksimum, równe 1 bitowi, osiąga dla 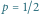
Gdy zadamy pytanie pół na pół, to niezależnie od odpowiedzi dowiadujemy się 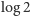 czyli 1 bit informacji. A co gdy, powiedzmy, zadamy pytanie, na które prawdopodobieństwo odpowiedzi "tak" jest równe tylko
czyli 1 bit informacji. A co gdy, powiedzmy, zadamy pytanie, na które prawdopodobieństwo odpowiedzi "tak" jest równe tylko 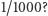 Jest niewielka szansa, że dowiemy się bardzo dużo
Jest niewielka szansa, że dowiemy się bardzo dużo 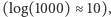 ale najprawdopodobniej dowiemy się niezbyt wiele. A sumarycznie, będzie lepiej czy gorzej? Zobaczmy!
ale najprawdopodobniej dowiemy się niezbyt wiele. A sumarycznie, będzie lepiej czy gorzej? Zobaczmy!

czyli bardzo niewiele! Zresztą, pół na pół średnio dostarcza najwięcej informacji.
Entropia jest też mocno związana z tym, jak dobrze potrafimy skompresować dane. Podstawowe twierdzenie Shannona mówi, że jeśli mamy ciąg  liter, każda niezależna od innych i z entropią
liter, każda niezależna od innych i z entropią 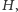 to nie możemy ich skompresować do długości krótszej niż
to nie możemy ich skompresować do długości krótszej niż  Choć stoją za tym pewne szczegóły techniczne, główną ideę można oddać, zliczając ciągi. Liczba słów o długości
Choć stoją za tym pewne szczegóły techniczne, główną ideę można oddać, zliczając ciągi. Liczba słów o długości 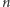 z alfabetu z
z alfabetu z  literami to
literami to 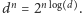 Jeśli chcielibyśmy zakodować owe słowa za pomocą zer i jedynek tak, by każde słowo miało swój kod binarny, potrzebujemy
Jeśli chcielibyśmy zakodować owe słowa za pomocą zer i jedynek tak, by każde słowo miało swój kod binarny, potrzebujemy  bitów. A co, jeśli nie wszystkie litery są równie często używane?
bitów. A co, jeśli nie wszystkie litery są równie często używane?
Gdy przesyłamy wiele liter, niektóre ciągi staną się skrajnie mało prawdopodobne. Dla ustalenia uwagi, zróbmy to na ciągu z zer i jedynek, z prawdopodobieństwami 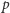 i
i 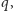 odpowiednio. Typowy ciąg o długości
odpowiednio. Typowy ciąg o długości  będzie miał
będzie miał 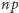 zer i
zer i 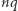 jedynek. Prawdopodobieństwo tego ciągu to
jedynek. Prawdopodobieństwo tego ciągu to 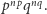 O ile, rzecz jasna, często można otrzymać ciągi z mniejszą lub większą liczbą zer i jedynek, to czym dłuższy ciąg, tym udział zer i jedynek będzie się bardziej zbliżał do
O ile, rzecz jasna, często można otrzymać ciągi z mniejszą lub większą liczbą zer i jedynek, to czym dłuższy ciąg, tym udział zer i jedynek będzie się bardziej zbliżał do 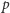 i
i 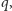 odpowiednio; innych ciągów jest skrajnie niewiele. Skoro typowe ciągi są mniej więcej równoprawdopodobne, a całkowite prawdopodobieństwo musi się sumować do jedności, to liczba tych typowych ciągów to około
odpowiednio; innych ciągów jest skrajnie niewiele. Skoro typowe ciągi są mniej więcej równoprawdopodobne, a całkowite prawdopodobieństwo musi się sumować do jedności, to liczba tych typowych ciągów to około 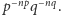 Czyli potrzebujemy
Czyli potrzebujemy

bitów do ich opisu. Przy obliczaniu prawdopodobieństwa jesteśmy dość liberalni - wszak np. dla 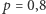 i
i  zamiana nawet jednego znaku zmienia prawdopodobieństwo o czynnik 4.
zamiana nawet jednego znaku zmienia prawdopodobieństwo o czynnik 4.
Niemniej, jest to kompensowane przez niewielkie zmiany 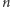 (czasem potrzeba kilku mniej lub więcej bitów do zakodowania owego ciągu). Innymi słowy, liczba typowych ciągów zer i jedynek rośnie jak
(czasem potrzeba kilku mniej lub więcej bitów do zakodowania owego ciągu). Innymi słowy, liczba typowych ciągów zer i jedynek rośnie jak 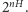
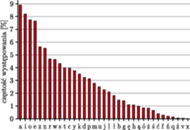
Częstość występowania liter w języku polskim, na podstawie Korpusu IPI PAN
Zastosowania? Zobaczmy, jak dobrze można skompresować tekst! W języku polskim używa się  liter (wliczając q, x i v z zapożyczonych słów). Jednak niektóre litery występują znacznie częściej niż inne, np. a stanowi 9% liter, podczas gdy ź - tylko 0,06%. Możemy obliczyć, że entropia liter to
liter (wliczając q, x i v z zapożyczonych słów). Jednak niektóre litery występują znacznie częściej niż inne, np. a stanowi 9% liter, podczas gdy ź - tylko 0,06%. Możemy obliczyć, że entropia liter to 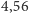 bitów. Dla porównania, taką samą entropię jak litery w języku polskim miałby hipotetyczny język z tylko
bitów. Dla porównania, taką samą entropię jak litery w języku polskim miałby hipotetyczny język z tylko 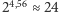 równo występującymi literami. Ale jak to się ma do kompresji? Porównując entropię z
równo występującymi literami. Ale jak to się ma do kompresji? Porównując entropię z 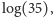 możemy zobaczyć, że, gdy znamy częstość znaków, potrafimy skompresować tekst do 89% objętości. W praktyce kompresja tekstu jest znacznie lepsza - zarówno dlatego, że nieskompresowany znak zwykle zajmuje
możemy zobaczyć, że, gdy znamy częstość znaków, potrafimy skompresować tekst do 89% objętości. W praktyce kompresja tekstu jest znacznie lepsza - zarówno dlatego, że nieskompresowany znak zwykle zajmuje 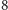 bitów (tu możemy kompresować do
bitów (tu możemy kompresować do 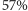 ), jak i to, że znaki nie są losowe, tj. łączą się w sylaby, słowa, a te - w teksty, które często używają podobnych słów.
), jak i to, że znaki nie są losowe, tj. łączą się w sylaby, słowa, a te - w teksty, które często używają podobnych słów.
Jako autor wiem, że ten tekst był skompresowany, ale, mam nadzieję, przekazał jakąś informację o entropii.
 np. rzutu nieuczciwą monetą (
np. rzutu nieuczciwą monetą ( 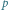 to prawdopodobieństwo orła) lub odpowiedzi na pytanie (
to prawdopodobieństwo orła) lub odpowiedzi na pytanie ( 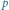 to prawdopodobieństwo "tak"). Maksimum, równe 1 bitowi, osiąga dla
to prawdopodobieństwo "tak"). Maksimum, równe 1 bitowi, osiąga dla 
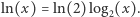 Np. dla podstawy
Np. dla podstawy  jednostką jest nit.
jednostką jest nit. jako
jako  równoważnie, ale, moim zdaniem, mniej dydaktycznie.
równoważnie, ale, moim zdaniem, mniej dydaktycznie.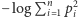 również ma opisaną obok własność addytywności. Ma ją także cała rodzina entropii Rényiego, będących uogólnieniem entropii Shannona, przy czym nie mają one interpretacji jako informacja.
również ma opisaną obok własność addytywności. Ma ją także cała rodzina entropii Rényiego, będących uogólnieniem entropii Shannona, przy czym nie mają one interpretacji jako informacja. np. rzutu nieuczciwą monetą (
np. rzutu nieuczciwą monetą ( 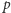 to prawdopodobieństwo orła) lub odpowiedzi na pytanie (
to prawdopodobieństwo orła) lub odpowiedzi na pytanie ( 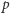 to prawdopodobieństwo "tak"). Maksimum, równe 1 bitowi, osiąga dla
to prawdopodobieństwo "tak"). Maksimum, równe 1 bitowi, osiąga dla